Вариант 16

1) Понятие интегральной суммы

Пусть на отрезке [а, b] задана неотрицательная функция у = f (x). Требуется найти площадь S криволинейной трапеции, ограниченной кривой у = f (x), прямыми х = a, x = b и осью абсцисс у = 0. При решении вышеприведённых задач наметился общий подход к решению этих задач. Введем в рассмотрение ломаную линию, которая расположена достаточно близко к кривой у = f (x) на [a, b] (см. рисунок 1). Фигура под ломаной состоит из прямоугольников, и ее площадь S_n, равная сумме площадей этих прямоугольников, может быть вычислена с использованием известных формул планиметрии. Поскольку ломаная выбрана достаточно близко к кривой y = f(x), то справедливо приближенное равенство S ≈ S_n. Это равенство оказывается тем более точным, чем ближе ломаная к исходной кривой. Поэтому в качестве искомой площади S можно взять предел площади ступенчатой фигуры S_n в предположении неограниченного приближения ломаной к заданной кривой. Пусть на отрезке [а, b] заданна функция у = f(x). Разобьем отрезок [а, b] на n элементарных отрезков точками x₀, x₁,…, x_n:a = x₀ < x₁ < x₂ < … < x_n = b. На каждом отрезке [x_i_{- 1}, x_i] разбиения выберем некоторую точку ξ _i и положим Δ x_i = x_i - x_i_{- 1}, где i = 1, 2,…, n. Сумму вида

будем называть интегральной суммой для функции у = f(x) на [а, b]. Очевидно, что интегральная сумма зависит как от способа разбиения отрезка [а, b] точками x₀, x₁,…, x_n, так и от выбора точек ξ₁, ξ₂, … ξ_n на каждом из отрезков разбиения [x _i_{- 1}, x_i], i = 1, 2, …, n.

Определение определённого интеграла

Если существует конечный предел I интегральной суммы при λ → 0, и он не зависит от способа выбора точек ξ _i, способа разбиения отрезка, то этот предел называется определенным интегралом от функции f (x)по отрезку [a, b] и обозначается следующим образом:

или

В этом случае функция f (x) называется интегрируемой на [a, b]. Числа a и b называются соответственно нижним и верхним пределами интегрирования, f (x) – подынтегральной функцией, х – переменной интегрирования. Следует заметить, что не имеет значения, какой буквой обозначена переменная интегрирования определенного интеграла

поскольку смена обозначений такого рода никак не влияет на поведение интегральной суммы. Несмотря на сходство в обозначениях и терминологии, определенный и неопределенный интегралы различны: в то время как

представляет семейство функций, определённый интеграл

есть число.

Связь определенного и не определенного интеграла

Это – формула Ньютона-Лейбница. Она связывает определенный интеграл с неопределенным.

Для вычисления определенного интеграла эта формула обычно з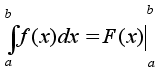 аписывается в виде

где знак служит символическим обозначением разности между значениями первообразной функции F(b) и F(а).

приложения определенного интеграла

Площадь криволинейной трапеции, ограниченной графиком функции , прямыми х = а, х = b и осью Ох, вычисляется по формуле

(64)

Если , то .

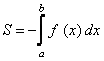Пусть и – непрерывные на функции и при любом . Тогда площадь фигуры, ограниченной графиками функций , вычисляется по формуле

. (65)

Действительно, если функции , то данная формула является очевидным следствием того, что площадь фигуры равна разности площадей криволинейных трапеций (рис. 14)