2.5.Определение точки обрыва верхней рабочей арматуры

Верхний продольный рабочий стержень каркаса ригеля обрывается в соответствии с изменением огибающей эпюры моментов.

Определяем относительную высоту сжатой зоны по формуле:

,

По таблице 3.1 [1] определяем ₁ = 0,917.

Вычисляем изгибающий момент, воспринимаемый сечением 1–1:

M₁ = R_sA_s2h₀ζ₁ = 365·10³·7,6·10^-4·0,64·0,917  162,8 кН·м.

Расстояние z от точки опирания ригеля до точки теоретического обрыва арматуры определяем из уравнения момента от нагрузки на ригель:

,приравняв значения M = M₁ = 162,8 кН·м.

Решив это уравнение, получаем z = 1,7 м.

Обрываемые стержни заводятся за точку теоретического обрыва на длину анкеровки ω, определяемую из условий:

1) ω ≥ 20d, ω ≥ 20·2,2 = 44 см;

2) , где:

Q_i = Q – q  z — поперечная сила в точке теоретического обрыва арматуры ригеля,

Q_i = 170,35 – 58,74  1,7 =70,492 кН; q_sw=200,18 кН/м — погонное усилие в поперечных стержнях (см. расчет поперечного армирования ригеля

м.

Выбираем большее значение и округляем до целого числа ω = 40 см.

2.6.Расчет прочности наклонных сечений

Коэффициенты _f, учитывающий наличие полок тавровых сечений, и _n, учитывающий влияние продольных сил, для ригеля равны 0, т.к. сечение ригеля — прямоугольное, арматура в ригеле ненапрягаемая.

Тогда коэффициент k:

k = 1 + 0 + 0 = 1 1,5.

Находим величину Q_bmin:

Q_bmin =_b3·k·R_bt·b·h₀ = 0,6·1·1,05·10³·0,3·0,64  120,96 кН.

Вычисляем M_b:

M_b = _b2·k·R_bt·b·h₀² = 2·1·1,05·10³·0,3·0,64²  258,05 кН·м.

Определяем максимальны шаг поперечных стержней:

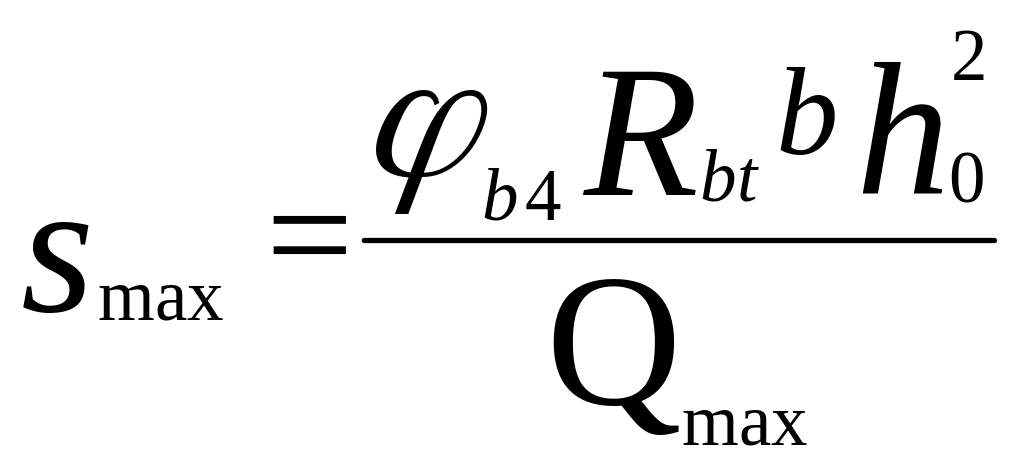
м.

Назначаем шаг s поперечных стержней на приопорных участках длиной l_риг/4 = 6400/4 = 1600 мм, исходя из условий:

, см;

s  50 см;

s  s_max = 1,13 см.

Принимаем s=20 см. Арматура, исходя из условий сварки с продольной, класса A-III диаметром Ø10 мм с R_sw = 255 МПа (т.к. d_sw/d  0,55  1/3 — приложение 5 [1]).

Погонное усилие в поперечных стержнях:

кН/м.

Проверяем условие :

кН/м.

Т.к. значение кН/м  0,56·q_sw = 120,108 кН/м, то расстояние от точки опоры до вершины наклонной трещины определяется:

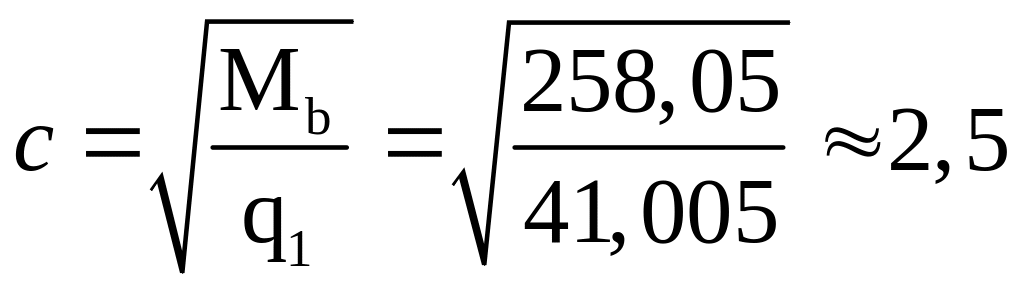м.

Находим величину c_max:

м.

Проверяем условие c  c_max: 2,31 м = c > c_max = 2,13 м — условие не выполняется, поэтому принимаем c = 2,13 м.

Вычисляем поперечное усилие, воспринимаемое бетоном сжатой зоны над вершиной наклонного сечения:

кН  Q_bmin = 120,96 кН — условие выполняется.

Поперечная сила в вершине наклонного сечения:

Q = 170,35 – 41,005 · 2,13  82,91 кН.

Вычисляем значение :

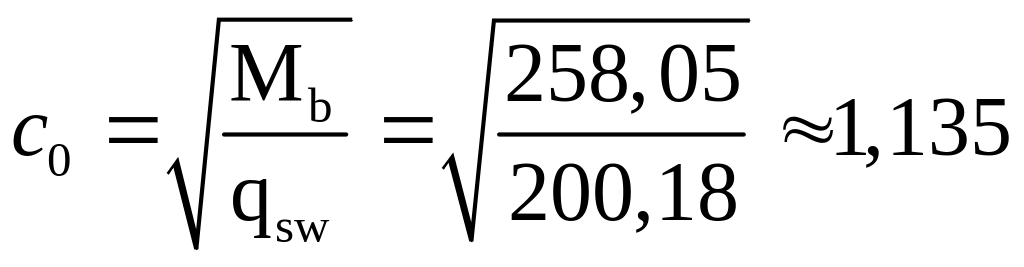м.

и проверяем условия: c₀  c = 2,13 м;

c₀  2h₀ = 2·0,64 = 1,28 м;

c₀  h₀ = 0,64 м.

Определяем сумму осевых усилий в поперечных стержнях:

Q_sw = q_sw·c₀ = 200,18·1,135  227,2 кН.

Проверяем условие прочности:

Q  Q_b + Q_sw, 82,91 120,96+227,2 = 348,17 кН.

Определяем параметр _sw:

.

Находим коэффициент :

.

Проверяем прочность по сжатой полосе между наклонными трещинами. Вычисляем коэффициент _w1, учитывающий влияние поперечных стержней балки:

_w1 = 1 + 5_sw = 1 + 5·6,67·2,617·10^-3  1,087  1,3.

Находим коэффициент _b1 по формуле:

_b1 = 1 – ·R_b=1 – 0,01·14,5  0,855.

Проверяем условие:

0,3_w1_b1R_bbh₀ = 0,3·1,087·0,855·14,5·10³·0,3·0,64 = 776,23 кН  Q = 170,35 кН — условие выполняется.

Т.к. c = 2,5 м  l₁ = l/4 = 1,6 м, то необходима проверка прочности наклонных сечений в средней части пролета ригеля. Шаг стержней поперечного армирования в средней части пролета равен: s = 3h/4 = 3·60/4 =45 см — принимаем s = 50 см.

Погонное усилие в поперечных стержнях:

кН/м.

Вычисляем значение:

м

и проверяем условия: c₀  c = 2,5 м;

c₀  h₀ = 0,64 м.

Определяем сумму осевых усилий в поперечных стержнях:

Q_sw = q_sw2·c₀ = 80,07·1,8  144,13 кН.

Проверяем условие:

Q  Q_b + Q_sw, 156,04  120,96 + 227,2 = 348,16 кН

Итак, на приопорных участках длиной 1600 мм устанавливаем арматуру Ø10 A-III с шагом 200 мм, а в средней части пролета — с шагом 500 мм._________________________