1.8.Расчет прочности наклонных сечений

Определяем коэффициент _f, учитывающий наличие полок тавровых сечений:

,

где b_f^/ – b  3h_f^/, 1,560 – 0,16 = 1,4  3 · 0,05 = 0,15 м — принимаем b_f^/ – b = 0,15 м.

< 0,5 —условие выполняется.

Определяем _n — коэффициент учитывающий влияние продольных сил:

, где P, усилие предварительного обжатия:

Н.

.

Вычисляем коэффициент k:

k = 1 + _n + _f  1,5,

k = 1 + 0,13 + 0,5 = 1,63 — принимаем k = 1,5.

Находим величину Q_bmin:

Q_bmin = _b3·k·R_bt·b·h₀,

Q_bmin = 0,6·1,5·0,9·10³·0,16·0,27 = 34,992 кН.

Вычисляем M_b:

M_b = _b2·k·R_bt·b·h₀² = 2·1,5·0,9·10⁶·0,16·0,27² = 31492,8 Н·м = 31,4928 кН·м. !!!!!!!

Определяем максимальны шаг поперечных стержней:

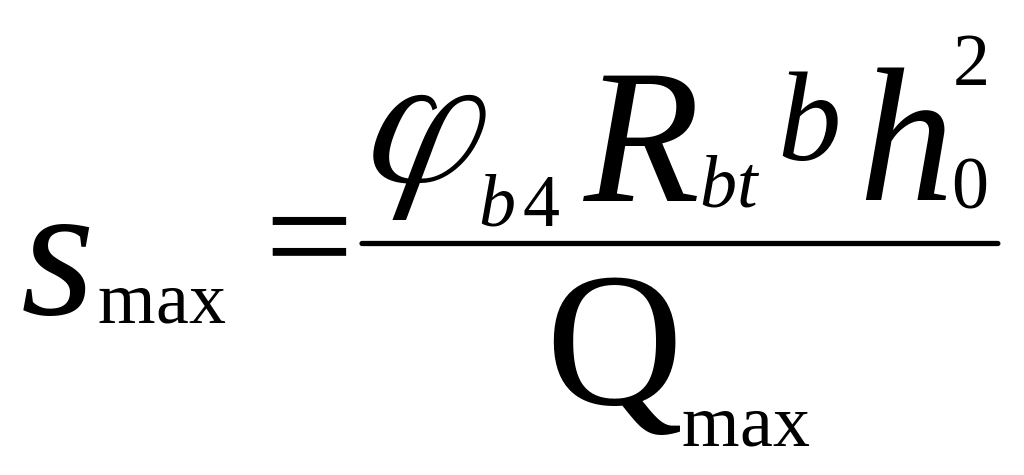
м.

Коэффициенты _b2, _b3 и _b4 определены по таблице 3.2 [1].

Назначаем шаг s поперечных стержней на приопорных участках длиной

l_р/4 = 5100/4 = 1275 мм, исходя из условий:

, см;

s  15 см;

s  s_max = 35 см.

Принимаем s = 10 см. Арматура класса Вр-I диаметром 5 мм с R_sw = 265 МПа.

Погонное усилие в поперечных стержнях:

Н/м  103,35 кН/м

Проверяем условие:

, кН/м.

Т.к. значение q = q₁ = 9,54 кН/м  0,56· 57,876 кН/м, то расстояние от точки опоры до вершины наклонной трещины определяется по формуле:

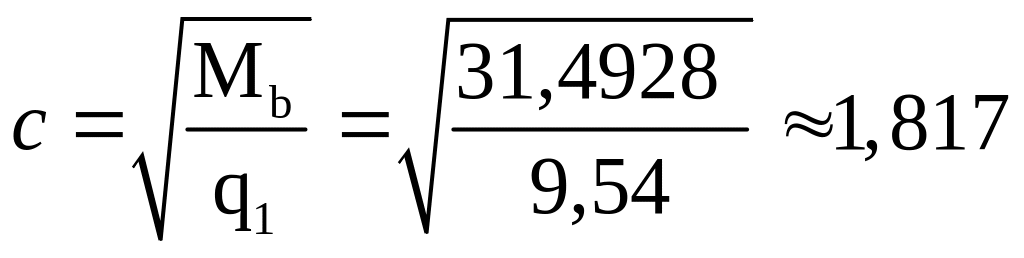м.

Находим величину:

м.

Проверяем условие c  c_max: м = c  c_max = м — условие не выполняется, поэтому принимаем c = c_max = м.

Поперечная сила в вершине наклонного сечения:

Q = Q_max – q · c = –9,54·  36,394.

Проверяем условие:

кН > Q_bmin=34,992 кН

Длинна проекции расчетного наклонного сечения:

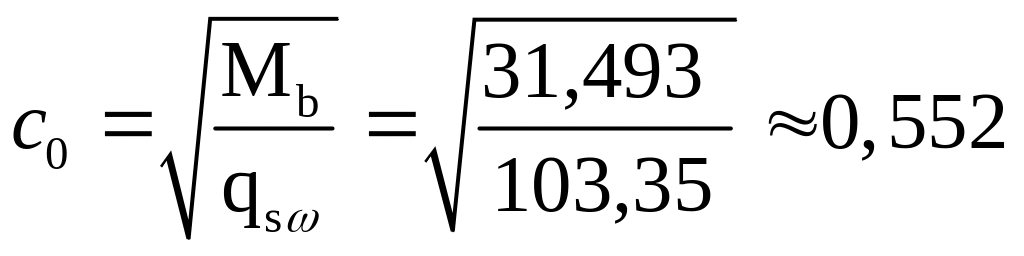м > = м, принимаем = м.

При этом: кН

Условие прочности: кН > Q=37,00 кН- обеспечивается.

Прочность проверяют по сжатой наклонной полосе: Определяем параметр .

Находим коэффициент .

Вычисляем коэффициент _w1, учитывающий влияние поперечных стержней балки:

_w1 = 1 + 5_sw = 1 + 5· · 1,077 < 1,3.

Находим коэффициент:

_b1 = 1 – ·R_b = 1 – 0,01 · 0,9  0,991, где коэффициент =0,01 для тяжелого бетона.

Проверяем условие прочности:

Q_max  0,3_w1_b1R_bbh₀,

0,3·_w1·_b1·R_b·b·h₀=0,3·1,077·0,991·11,5·10⁶·0,18·0,27=178 955 НQ_max = 53 460 Н — условие выполняется.

Итак, на приопорных участках длиной 1275 мм устанавливаем арматуру Ø5 Вр-I с шагом 10 см, а в средней части пролета — с шагом 25 см.

1.9.Расчеты панели перекрытия по II-й группе предельных состояний

1.9.1.Определение геометрических характеристик приведенного сечения.

Площадь приведенного сечения:

,

— отношение модулей упругости,

= 1167,82см².

Статический момент площади приведенного сечения:

S_red = A_iy_i = 156·5·27,5+25·16·12,5+7,037·5,09·3 = 26450 см³.

Расстояние от нижней грани до центра тяжести приведенного сечения:

см.

Момент инерции приведенного сечения, относительно оси, проходящей через центр тяжести сечения:

= 84264,06 см⁴.

Момент сопротивления приведенного сечения по нижней зоне:

см³.

Момент сопротивления приведенного сечения по верхней зоне:

см³.

Расстояние от ядровой точки, наиболее удаленной от растянутой зоны, до центра тяжести сечения:

, где .

Отношение напряжения в бетоне от нормативных нагрузок и усилия обжатия к расчётному сопротивлению бетона (_bp/R_b,ser) для предельных состояний второй группы предварительно принимаем равным 0,75. Тогда:

, см.

Расстояние от ядровой точки, наименее удалённой от растянутой зоны, до центра тяжести сечения:

см.

Упругопластический момент сопротивления сечения по растянутой зоне: , где  = 1,75 — значение коэффициента, учитывающего влияние неупругих деформаций бетона растянутой зоны, для тавровых сечений с полкой в сжатой зоне.

W_pl = 1,75· = 6510,47см³.

Упругопластический момент сопротивления сечения по растянутой зоне в стадии изготовления и обжатия:

см³,

где : , — принимаем  = 1,5.