Указания к выполнению контрольной работы №2 Тема 8. Неопределенный интеграл.

[1] c. 256 – 258 примеры 10.1 (а – в), 10.2 (а – д), 10.3 (а – г),

с. 259 – 262 примеры 10.4 – 10.9, с. 263 – 265 примеры 10.10 – 10.12,

с. 269 – 271 примеры 10.14 – 10.15, с. 272 – 273 примеры 10.16 – 10.18,

с. 274 – 275 примеры 10.19 – 10.22.

[5] c. 209 – 210 № 1328 – 1336, с. 213 – 215 № 1360 – 1367,

с. 216 – 218 № 1385 – 1391, с. 219 – 220 № 1403 – 1407,

с. 223 – 228 № 1419 – 1426, с. 229 – 232 № 1444 – 1452,

с. 234 – 240 № 1472 – 1488.

[11], с. 320 примеры 1 – 5, с. 322 примеры 1 – 6, с. 323 – 325

примеры 1 – 3, с. 326 – 328 примеры 1 – 6, с. 331 пример 2, с. 334

пример 1, с. 336 – 337 примеры 1 – 3, с. 338 примеры 1, 2, с. 341

пример 3, с. 342 – 345 примеры 1 – 7, с. 346 – 347 пример 1.

Основные правила интегрирования:

1. 

2. 

3. 

Таблица основных интегралов:

6

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 11. Путем преобразований свести интегралы к табличным:

Решение. Применим правила интегрирования 3 и 2, далее преобразуем подынтегральные функции каждого полученного интеграла, после чего воспользуемся табличными интегралами 1,2,9:

 Преобразуем подынтегральную функцию и представим заданный интеграл в виде суммы двух других, каждый из которых табличный:

Чтобы привести данный интеграл к табличному, представим стоящую в числителе единицу по основному тригонометрическому свойству как

и разделим почленно на знаменатель:

Если данный интеграл не является табличным и не может быть найден способом непосредственного интегрирования, то во многих случаях введение новой переменной интегрирования позволяет свести данный интеграл к табличному интегралу. В этом сущность метода подстановки.

Задача 12. Применяя соответствующие подстановки, вычислить указанные интегралы:

Решение.

Интегрирование по частям называется нахождение интеграла по формуле: где непрерывно дифференцируемые функции от Этой формулой пользуются в тех случаях, когда интеграл есть более простой по сравнению с заданным интегралом

При этом за берется та функция, которая при дифференцировании упрощается, а за та часть подынтегрального выражения, интеграл от которой известен или может быть найден.

Пользуясь формулой интегрирования по частям, весьма важно правильно выбрать множители и Для разложения подынтегрального выражения на указанные множители нет общих правил, но можно руководствоваться некоторыми частными указаниями.

Указание 1. Если подынтегральное выражение содержит произведение показательной или тригонометрической функции на многочлен, то за множитель следует принять многочлен:

где многочлен. Во всех трех интегралах полагают , а за в первом интеграле полагают ; во втором и третьем интегралах соответственно и

Указание 2. Если подынтегральное выражение содержит произведение логарифмической или обратной тригонометрической функции на многочлен, то за множитель следует принять логарифмическую функцию или обратную тригонометрическую функцию:

Во всех трех интегралах полагают за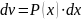 , а за соответственно

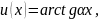
Задача 13. Пользуясь формулой интегрирования по частям, найти интегралы:

Решение.

Интегрирование рациональных дробей с помощью разложения на простейшие дроби. При интегрировании рациональной дроби надо сделать следующие алгебраические преобразования:

1) если дана неправильная рациональная дробь, то выделить из нее целую часть, т.е. представить в виде

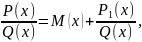
где многочлен, а правильная рациональная дробь;

2) разложить знаменатель дроби на множители;

3) правильную рациональную дробь разложить на сумму простейших дробей.

Задача 14. Вычислить интеграл:

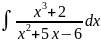
Решение.

Выделим целую часть:

Итак, получаем

Разложим подынтегральную функцию на сумму простейших дробей:

Приведем правую часть к общему знаменателю:

Приравнивая числители, получаем

или Приравнивая справа и слева в полученном равенстве коэффициенты при одинаковых степенях , получим систему

Следовательно,

Вернемся к вычислению интеграла:

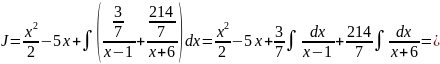
Рассмотрим случай, когда квадратный трехчлен знаменателя не имеет действительных корней. Основной прием вычисления такого интеграла состоит в том, что квадратный трехчлен дополняют до полного квадрата.

Задача 15. Вычислить интеграл:

Решение.

Вопросы для самопроверки

1. Сформулируйте определение первообразной функции.

2. Что называется неопределенным интегралом от данной функции?

3. Перечислите основные свойства неопределенного интеграла.

4. Напишите формулы таблицы основных интегралов.

5. В чем сущность метода интегрирования заменой переменной?

6. Напишите формулу интегрирования по частям в неопределенном интеграле.