Тема 2. Векторная алгебра и аналитическая геометрия в пространстве.

[1] глава 3, §3.1, c. 63 – 67, с. 67 – 68 пример 3.1.

[5] глава 2, §2, с. 45 – 47, с. 47 – 48 №243 – 245, с. 50 №259, с.55 №288.

[7] с. 22 §1.5 пример 1, с. 64 пример 1.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 2. Даны координаты точек: А(3;0; –5), В(6;2;1), С(12; –12;3).

Требуется: 1) записать векторы в системе орт и найти модули этих векторов; 2) вычислить угол между векторами ; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору .

Решение. 1. Если даны точки и , то вектор через орты выражается следующим образом:

Подставляя в эту формулу координаты точек А и В, имеем:

Аналогично определяем координаты вектора

Модуль вектора вычисляется по формуле:

Подставим в формулу (2) координаты векторов получим модули этих векторов:

2. Косинус угла , образованного векторами , равен их скалярному произведению, деленному на произведение модулей этих векторов, т.е.

Скалярное произведение векторов вычислим по формуле: В результате будем иметь . Исходя из формулы (3), имеем:

3.  Уравнение плоскости, проходящей через точку , перпендикулярно вектору , имеет вид:

По условию задачи искомая плоскость проходит через точку С(12; перпендикулярно вектору Подставляя в формулу (4) данные задачи, получим:

– искомое уравнение плоскости.

Вопросы для самопроверки.

1. Какие величины называются скалярными? Что называется вектором?

2. Какие вектора называются коллинеарными?

3. Какие вектора называются равными?

4. Какие существуют операции над векторами?

5. Как определить координаты вектора, если известны координаты начала и конца вектора?

6. Дайте определение скалярного произведения двух векторов. Перечислите основные свойства скалярного произведения.

7. Запишите скалярное произведение в координатной форме.

8. Напишите формулу для вычисления угла между двумя векторами.

9. Сформулируйте условия коллинеарности и перпендикулярности векторов.

10. Напишите общее уравнение плоскости.

11. Напишите уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.

12. Напишите уравнение плоскости, проходящей через три данные точки.

13. Напишите формулу для определения расстояния от точки до плоскости.

Тема 3. Элементы линейной алгебры

[1] глава 1, с.15 пример 1.5, с. 20 пример 1.7, с. 28 пример 1.10,

Глава 2, с. 42 пример 2.1, с.46 примеры 2.2 – 2.3, с.49 пример 2.4.

[2] с. 35 – 39 № 2.1 – 2.5, с. 42 – 43 № 2.35, 2.36.

[5] c.89 № 438 – 439, с.90 № 440, с.92 № 444 – 445.

Рассмотрим систему трех уравнений с тремя неизвестными:

Для коэффициентов системы введена двойная индексация, т.е. у коэффициентов первый индекс означает номер уравнения, а второй – номер неизвестного.

Решим систему методом Гаусса. Пусть для определенности

Первый шаг. Разделим все члены первого уравнения на 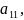умножаем полученное уравнение на и вычтем из него второе уравнение системы; затем умножаем первое уравнение на и вычтем из него третье уравнение системы. В результате первого шага приходим к системе:

Второй шаг. Второе уравнение системы (2) разделим на , после этого полученное уравнение умножим на и вычтем из него третье уравнение системы. В результате второго шага приходим к системе:

Из полученной системы последовательно определяем все неизвестные.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 3. Решить систему линейных уравнений:

а) методом Гаусса; б) с помощью обратной матрицы.

Решение. а) Исключим из последних двух уравнений х₁. Для этого умножим первое уравнение на (–5) и результаты прибавим соответственно ко второму уравнению, затем обе части первого уравнения умножим на (–3) и результаты прибавим к третьему уравнению. В результате получим систему, эквивалентную данной:

Разделив обе части второго уравнения системы (1) на 2, получим систему

Теперь исключим из третьего уравнения системы (2) переменную х₂. Для этого обе части второго уравнения этой системы умножим на (-7) и результаты прибавим к третьему уравнению. В результате получим систему

Откуда x₃ = 3, х₂ = 1 и х₁ = -2. Приведение данной системы к ступенчатому виду (3) практически более удобно, если использовать преобразования расширенной матрицы данной системы, т. е. матрицы, составленной из коэффициентов при неизвестных и свободных членов. Для удобства столбец свободных членов этой матрицы отделим вертикальной чертой. Расширенная матрица данной системы имеет вид

.

Умножим элементы первой строки матрицы на (–5) и результаты прибавим к элементам второй строки, затем умножим элементы первой строки на (–3) и результаты прибавим к элементам третьей строки. Получим матрицу

Разделив элементы второй строки на 2, получим

Элементы второй строки умножим на (–7) и результаты прибавим к элементам третьей строки. Получим матрицу,

которая позволяет данную систему привести к виду (3) и затем решить ее.

б) Введём обозначения: , и . Тогда систему уравнений можно представить в виде матричного уравнения , которое решим по формуле: . Найдём по следующему алгоритму:

1) вычислить определитель матрицы А, т.е. Δ = det(A);

2) вычислить алгебраические дополнения всех элементов определителя и составить матрицу из алгебраических дополнений:

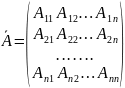, где , где

3) Полученную матрицу транспортируем: .

4) обратную матрицу определим из формулы:

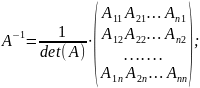
5) выполним проверку:

Реализуем данный алгоритм.

1) . При этом условии обратная матрица существует.

2) вычислим алгебраические дополнения элементов матрицы по формуле: , где 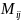- определитель, полученный из путём вычёркивания -ой строки и -го столбца.

. Аналогично вычисляем все остальные алгебраические дополнения.

, , , , , , , .

В результате получим матрицу

3) Транспортируем полученную матрицу:. .

4) Тогда обратная матрица имеет вид:

5) Выполним проверку, покажем, что 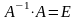, где - единичная матрица.

.

Теперь найдём решение матричного уравнения:

. Тогда решение системы: .

Вопросы для самопроверки

1. Что называется определителем второго, третьего, n-го порядков?

2. Назовите основные свойства определителей.

3. Что называется минором, алгебраическим дополнением элемента определителя?

4. Приведите схему решения системы линейных уравнений по методу Гаусса.

5. Что называется матрицей?

6. Как определяются основные действия над матрицами?

7. Какая матрица называется обратной по отношению к данной матрице? Как найти матрицу, обратную данной?

8. Что называется рангом матрицы? Как вычислить ранг матрицы?

9. Сформулируйте теорему Кронекера-Капелли.

10.Опишите матричный способ решения системы линейных уравнений.