
- •Методические указания и контрольные задания по высшей математике для студентов-заочников экономических специальностей агау
- •Общие методические указания
- •Указания к выполнению контрольной работы № 1 Тема 1. Аналитическая геометрия на плоскости
- •Тема 2. Векторная алгебра и аналитическая геометрия в пространстве.
- •Тема 3. Элементы линейной алгебры
- •Глава 2, с. 42 пример 2.1, с.46 примеры 2.2 – 2.3, с.49 пример 2.4.
- •Тема 4. Введение в анализ.
- •Тема 5. Производная и дифференциал функции.
- •Тема 6. Приложения производной.
- •Тема 7. Функции нескольких переменных.
- •Указания к выполнению контрольной работы №2 Тема 8. Неопределенный интеграл.
- •Тема 9. Определенный интеграл.
- •Тема 10. Дифференциальные уравнения.
- •Тема 11. Ряды.
- •Указания к выполнению контрольной работы №3. Тема 12. Повторные независимые испытания.
- •Тема 13. Случайные величины и их характеристики.
- •Тема 14. Элементы линейного программирования.
- •Графический метод решения.
- •Аналитический метод решения.
- •Задачи для контрольных работ Контрольная работа №1
- •Контрольная работа №2.
- •Контрольная работа №3.
- •Литература
Контрольная работа №2.
В задачах 181 – 200 найти указанные неопределенные интегралы и результаты интегрирования проверить дифференцированием.
181.
а) ;
б)
;
б)
 ;
в)
;
в)
 .
.
182.
а)
 ;
б)
;
б)
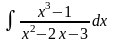 ;
в).
;
в).
183. а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
184.
а)
 ;
б)
;
б)
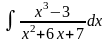 ;
в)
;
в)
 .
.
185.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
186.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
187.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
188.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
189.
а)
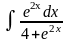 ;
б)
;
б)
 ;
в)
;
в)
 .
.
190.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
191.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
192.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
193.
а)
 ;
б)
;
б)
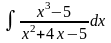 ;
в)
;
в)
 .
.
194. а)
 ;
б)
;
б)
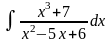 ;
в)
;
в) .
.
195. а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
196. а)
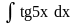 ;
б)
;
б)
 ;
в)
;
в)

197. а)
 ;
б)
;
б)
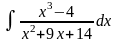 ;
в)
;
в)

198. а)
 ;
б)
;
б)
 ;
в)
.
;
в)
.
199. а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
200. а)
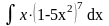 ;
б)
;
б)
 ;
в)
;
в)
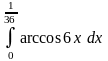 .
.
В задачах 201 – 210 вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж.
201.
 .
.
202.  .
.
203.  .
.
204.  .
.
205.  .
.
206.  .
.
207.
 .
.
208.  .
.
209. 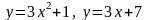 .
.
210.  .
.
В задачах 211 – 215 вычислить объем тела, образованного вращением вокруг оси OX фигуры, ограниченной указанными линиями. Сделать чертеж.
211.  .
.
212.  .
.
213.  .
.
214.  .
.
215. 
В задачах 216 – 220 вычислить объем тела, образованного вращением вокруг оси OY фигуры, ограниченной указанными линиями. Сделать чертеж.
216.  .
.
217.  .
.
218.  .
.
219.  .
.
220.
 .
.
В задачах 221 – 240 определить частное решение дифференциального уравнения первого порядка, удовлетворяющее указанным начальным условиям.
221.
 222.
222.

223..
 224.
224.

225.
 226.
226.

227.
 228.
228.

229.
 230.
230.

231.
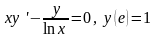 232.
232.

233.
 234.
234.

235.
 236.
236.

237.
 238.
238.
239. 240.
В задачах 241-260 определить общее решение (общий интеграл) дифференциальных уравнений первого порядка.
241.
 .
242.
.
242.
 .
.
243.
 .
244.
.
244.
 .
.
245.
 .
246.
.
246.
 .
.
247.
 .
248.
.
248.
 .
.
249.
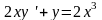 .
250.
.
250.
 .
.
251.
 252.
252.

253.
 254.
254.

255.
 256.
256.
257. 258.
259.
 260.
260.

В задачах 261 – 280 определить частное решение дифференциального уравнения второго порядка, удовлетворяющее указанным начальным условиям.
261.  .
.
262.  .
.
263.  .
.
264.
 .
.
265.
 .
.
266.
 .
.
267.
 .
.
268.
 .
.
269.
 .
.
270.
 .
.
271.

272.

273.

274.
275.
.

276.
.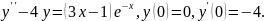
277.

278.
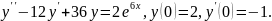
279.

280.

В
задачах 281 –
300 дан
степенной ряд
 .
При заданных значениях a
и b
написать первые три члена ряда, определить
интервал сходимости ряда и исследовать
его сходимость на концах интервала.
.
При заданных значениях a
и b
написать первые три члена ряда, определить
интервал сходимости ряда и исследовать
его сходимость на концах интервала.
281.
 .
282.
.
282.
 .
.
283.
 .
284.
.
284.
 .
.
285.
 .
286.
.
286.
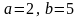 .
.
287.
 .
288.
.
288.
 .
.
289.
 .
290.
.
290.
 .
.
291.
 .
292.
.
292.
 .
.
293.
 .
294.
.
294.
 .
.
295.
 .
296.
.
296.
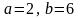 .
.
297.
 .
298.
.
298.
 .
.
299.
 .
300.
.
300.
 .
.
В задачах 301 – 320 вычислить определенный интеграл с точностью до 0,001 путем разложения подынтегральной функции в ряд и почленного дифференцирования этого ряда.
301.
 .
302.
.
302.
 .
.
303.
 .
304.
.
304.
 .
.
305.
 .
306.
.
306.
 .
.
307.
 .
308.
.
308.
 .
.
309.
 .
310.
.
310.
 .
.
311.
 .
312.
.
.
312.
.
313.
 .
314.
.
314.
 .
.
315.
 .
316.
.
316.
 .
.
317.
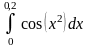 .
318.
.
318.
 .
.
319.
 .
320.
.
320.
 .
.
