28. Определение частных законов распределения по совместному (в общем, дискретном и непрерывном случаях). Пример для дискретного случая.

Рассмотрим общий случай:

Пусть F(x,y) – функция распределения случайного вектора Z = col(X,Y). В таком случае F_X=F(x,+¥); F_Y=F(+¥,y). В дискретном случае задача упрощается:

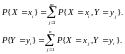
Решение находится по заданной таблице распределения. В непрерывном случае функция плотности распределения вероятности для СВ, составляющих вектор, находится следующим образом:

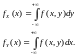
Пример: Предприятие имеет две поточные линии по сборке некоторой продукции. Технологические процессы на линиях связаны между собой. Пусть Х – количество единиц продукции, собранной за день первой линией, а Y – второй. Совместное распределение этих величин задано таблицей. Найти частные распределения СВ X и Y. Решение:

Y\X	0	1
0	1/8	0
1	1/4	1/8
2	1/8	3/8

Найдем частные законы распределения. Для этого просуммируем соответствующие значения по столбцам или строкам. Получим:

Для Х:

X	0	1
0	1/2	1/2

Для Y:

Y	0	1	2
0	1/8	3/8	1/2

29. Условия независимости случайных величин (в общем, дискретном и непрерывном случаях). Пример: независимость компонент случайного вектора, равномерно распределенного на прямоугольнике.

СВ X и Y называются независимыми, если F(x,y) = F_X(x)F_Y(y). Пусть Z – случайный двумерный дискретный вектор. Дискретные СВ X и Y, составляющие вектор Z, независимы тогда и только тогда, когда для всех i=0,n; j=0,m P{X = x_i, Y = y_i} = P{X = x_i}P{Y = y_i}. Для независимости непрерывных СВ Х и Y достаточно, чтобы выполнялось равенство f(x,y) = f_X(x)f_Y(y).

П ример: Случайный вектор Z распределен равномерно на прямоугольнике [1,1]x[2,3] и имеет функцию распределения ½(xy-x-y+1) на площади прямоугольника. Независимы ли его компоненты? Решение: Вектор по условию составлен из двух равномерно распределенных случайных величин X и Y. X ~ R(1,2); Y ~ R(1,3). f_X(x) = 1/(2-1) = 1 при X Î [1,2]. f_Y(y) = ½ при Y Î [1,3]. Если компоненты X и Y независимы, то f(x,y) = f_X(x)f_Y(y). Получаем следующее:

Теперь найдем функцию распределения, проинтегрировав f(x,y) по области прямоугольника.

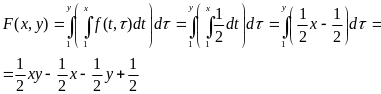
При Х, Y Î [1,1]x[2,3]. При X > 2, Y > 3 F(x,y) = 1. При X < 1, Y < 1 F(x,y) = 0. Полученная функция совпадает с заданной в условии. Компоненты независимы.

30. Моментные характеристики пары случайных величин: смешанный второй начальный момент, ковариация, коэффициент корреляции, ковариационная матрица. Свойства ковариации: вычисление ковариации через смешанный второй начальный момент, симметричность, линейность.

Смешанный второй начальный момент есть математическое ожидание произведения компонент вектора, т.е. n_XY = M[XY]. Если произвести преобразование по формуле для зависимых СВ, то M[XY] = (по определению) k_XY + M[X]M[Y], где k_XY – ковариация. Ковариацией (корреляционным моментом) k_XY СВ X и Y называется второй центральный смешанный момент. k_XY = (по определению) M[(X-M[X])(Y-M[Y])]. Ковариация непрерывных СВ X и Y равна:

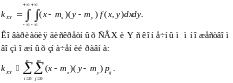
Ковариация нормированных СВ называется коэффициентом корреляции. r_XY=k_XY/s_XsY.

Ковариационная матрица:

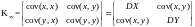
Свойства ковариации:

• cov(Ax,By)=ABcov(x,y).

cov(x,y) = cov(y,x).

31. Формула дисперсии суммы (разности) двух величин. Неравенство Коши-Шварца для ковариации.

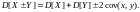
Пусть MX=MY=0. M[X±Y] = 0.

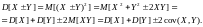
Неравенство Коши-Шварца:

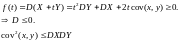
32. Некоррелированность и линейная зависимость двух случайных величин и их связь со свойствами ковариации и коэффициента корреляции.

СВ X и Y называются некоррелированными, если cov(X,Y)=0. Из независимости СВ следует их некоррелированность, однако обратное утверждение в общем случае ложно. Как пример можно разобрать функциональную зависимость Y = X², где X ~ R(-a,a). Тогда ковариация между X и Y равна:

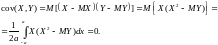
Величины не коррелированны, но связаны функциональной зависимостью. Коэффициент корреляции:

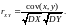
Заметим, что |r_XY| £ 1 (следует из неравенства Коши-Шварца).

Если |r_XY| = 1, то случайные величины X, Y линейно зависимы, т.е.

$ с₁, с₂ Î R, с₁²+с₂² > 0: с₁X + с₂Y = 0.

Линейная зависимость случайных величин X и Y или, что то же самое, их коллинеарность являются частным случаем их функциональной зависимости.