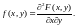14. Этапы определения математического ожидания. Вычисление математического ожидания в непрерывном и дискретном случаях.

Пусть плотность f(x) непрерывной СВ Х такая, что сходится интеграл

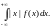Тогда число m_x = (по определению) M[X] = (по определению) 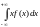будем называть математическим ожиданием (МО) непрерывной СВ Х. Для дискретной СВ Х с конечным числом значений математическое ожидание определяется следующим образом:

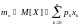, где p_k = (по определению) P{X = x_k}. Аналогично определяется МО дискретной СВ со счетным числом значений.

Пусть СВ Х непрерывна, а j(x) – некоторая скалярная функция скалярного аргумента. Тогда для СВ Y = (по определению) j(Х) МО СВ Y вычисляется следующим образом:

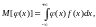
Если интеграл абсолютно сходится.

Если X – дискретная СВ с конечным множеством значений, то

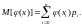
15. Вычисление математического ожидания в непрерывном и дискретном случаях. Примеры.

Для непрерывной СВ Х:

Для дискретной СВ Х с конечным числом значений:

Примеры: Найти математическое ожидание СВ Y = Х²-3X+2 с учетом, что плотность вероятности СВ X на отрезке [-1;1] задана функцией f(x)=(3/2)x² и равна нулю за пределами этого отрезка. Решение: Найдем математическое ожидание сразу по формуле.

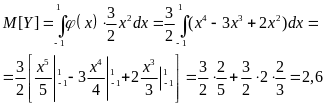
Найти математическое ожидание дискретной СВ Х, ряд распределения которой имеет вид:

Х	0	1	2	3
Р	0,1	0,2	0,3	0,4

Решение: Найдем математическое ожидание сразу по формуле.

16. Свойства математического ожидания: математическое ожидание константы, линейность, монотонность.

- M[C]=C. Действительно, пусть Х – дискретная СВ, принимающая с вероятностью 1 значение C. Тогда M[X] = (по определению) =CP{X=C}=C.

- M[CX]=CM[X], если C – константа. Действительно, пусть, например, Х – непрерывная СВ. Тогда

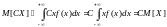
- М[X+C]=M[X]+C, если С – константа. Очевидно, что, например, для непрерывной СВ можно получить:

- Монотонность заключается в том, что в случае X £Y MX£MY.

17. Свойства математического ожидания неотрицательной случайной величины: неравенство Маркова, невырожденность.

Невырожденность математического ожидания заключается в том, что в случае, если M[|X|]=0, P(X=0)=1. Событие Х=0 можно представить как событие, что |X|<1/n при любом n > 0. Обратное же событие заключается в том, что существует такое n, при котором |X|³1/n.

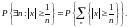
По свойству вероятности:

Произведя необходимые замены получим следующее неравенство, называемое неравенством Маркова.

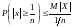
Данное неравенство выполняется для всех Х ³ 0. В общем случае константа 1/n имеет смысл любого положительного числа.

18. Формула умножения для математического ожидания. Математическое ожидание функции случайной величины.

Математическое ожидание произведения двух независимых случайных величин есть произведение математических ожиданий каждой из СВ. В В общем случае M[XY] = M[X]M[Y] + cov(X,Y). Для независимых СВ ковариация равна нулю.

Пусть СВ Х непрерывна, а j(x) – некоторая скалярная функция скалярного аргумента. Тогда для СВ Y = (по определению) j(Х) МО СВ Y вычисляется следующим образом:

Если интеграл абсолютно сходится.

Если X – дискретная СВ с конечным множеством значений, то

19. Моментные характеристики случайных величин: второй начальный момент, дисперсия, среднеквадратическое отклонение. Свойства дисперсии: неотрицательность, случай нулевой дисперсии, вычисление дисперсии через второй начальный момент, неравенство Ляпунова.

Второй начальный момент M[X²] вычисляется подобно первому начальному моменту. Для его вычисления просто воспользоваться свойством МО функции СВ. Пусть СВ Х непрерывна, а j(x) – некоторая скалярная функция скалярного аргумента. Тогда для СВ Y = (по определению) j(Х) МО СВ Y вычисляется следующим образом:

Если интеграл абсолютно сходится. В нашем случае j(x) = Х².

Если X – дискретная СВ с конечным множеством значений, то

Дисперсия СВ есть разность второго момента и квадрата математического ожидания. Дисперсия характеризует среднее отклонение СВ от МО. Среднеквадратическое отклонение есть квадратный корень из дисперсии СВ. Свойства дисперсии:

- D[C] = 0;

- D[CX] = C²DX;

- D[CX+B]= C²DX.

В случае, если D[X]=0, P(X=MX)=1. Доказывается по неравенству Чебышева.

Неравенство Ляпунова:

D[X] = M[X²] – (M[X])² ³ 0.

20. Свойства дисперсии: вычисление дисперсии для линейной функции случайной величины, неравенство Чебышева, «закон трех сигм».

Способ вычисления дисперсии для линейной функции случайной величины вытекает из свойств дисперсии.

D[kX+b] = D[kX] + D[b] + 2cov(kX,b) = kD[X].

Неравенство Чебышева:

Пусть C = k(D[X])^½. Тогда:

Для k = 3 это неравенство имеет название «закона трёх сигм», и заключается в том, что вероятность того, что случайная величина отклонится от математического ожидания больше чем на три величины среднеквадратического отклонения, равна 1/9.

21. Стандартные дискретные распределения: Бернулли, биномиальное, геометрическое.

Биномиальное распределение:

Дискретная СВ Х с реализациями x_k = k, k=0,n, имеет биномиальное распределение с параметрами n и р Î (0,1), если вероятность события Х = х_k определяется формулой Бернулли:

g(t) = ||бином Ньютона|| = (q+pe^it)ⁿ.

X ~ Bi(n,p). MX = np, DX = npq.

Распределение Бернулли:

Распределение Бернулли есть частный случай биномиального распределения при n = 1.

Y ~ Be(p). MY = p, DY = pq.

Геометрическое распределение:

Геометри́ческое распределе́ние в теории вероятностей — это распределение дискретной случайной величины равной количеству испытаний случайного эксперимента до наблюдения первого «успеха».

Пусть Х1,…,Xn – конечная последовательность случайных величин с распределением Бернулли. Построим случайную величину Y = min{i | X_i=1} – 1 (Количество «неудач» до первого «успеха»). Распределение случайной величины Y называется геометрическим с вероятностью «успеха» p.

Y ~ Geom(p). М[Y]=р/(1-qе^t). D[Y]=q/р²

22. Пуассоновское распределение: теорема Пуассона.

Теорема Пуассона: Между биномиальным распределением и распределением Пуассона имеется следующая связь: Пусть n ® µ, p ® 0 и при этом np º a = const. Тогда:

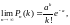
Где .

Доказывается эта теорема с использованием второго замечательного предела (1-a/n)ⁿ ® e^-a при n ® µ.

Дискретная СВ Х с реализациями xk = k, k = 0, 1, …, имеет распределение Пуассона с параметром a > 0, что символически записывается как Х ~ П(а), если

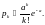
M[X] = D[X] = a.

23. Равномерное распределение. Пример: игла Бюффона.

СВ Х распределена равномерно на отрезке [a,b] (Х ~ R(a,b)), если плотность вероятности имеет вид 1/(b-a) при х Î [a,b] и 0 при х Ï [a,b]. Функция распределения имеет вид:

М[X] = (a+b)/2; D[X] = (b-a)²/12; M[X²] = (b²+ba+a²)/3.

Игла Бюффона. Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии h. На плоскость наудачу бросается игла длиной l (l < h). Найти вероятность того, что игла пересечет какую-либо прямую. Решение: Рассмотрим середину иглы. Расстояние от нее до ближайшей прямой обозначим за А. А распределена равномерно на [0;h/2]. Угол между иглой и прямой обозначим за a. a распределена равномерно на [0;p/2]. Тогда условие пересечения иглой прямой запишется в виде А £ (l/2)×sina. Площадь под графиком равна l/2. Искомая вероятность равна (по классической формуле) отношению площади под графиком к площади прямоугольника [0;p/2]x[0;h/2]. P=2l/ph.

24. Экспоненциальное распределение. Пример: распределение времени безотказной работы сложной технической системы.

СВ Х имеет экспоненциальное (показательное) распределение с параметром l > 0, т. е. X ~ E(l), если плотность вероятности имеет вид f(x) = lexp(-lx) при x > 0 и f(x) = 0 при x £ 0. Функция распределения СВ X ~ E(l) F(x) = 0 при x £ 0 и F(x) = 1 – exp[-lx] при x > 0.

M[X] = 1/l, D[X] = 1/l², M[X²] = 2/l².

Пример: Время X безотказной работы станка имеет экспоненциальное распределение. Вероятность того, что станок откажет за 5 часов работы равна 0,39347. Найти М[X], D[X], M[X²]. Решение: Найдем параметр распределения l. Для этого решим уравнение:

1 – exp[-5l] = 0,39347. exp[-5l] = 0,60653. -5l = ln(0,60653) = -0,5.

l = 0,1. Теперь найдем необходимые моментные характеристики.

M[X] = 1/l = 10,

D[X] = 1/l² = 100,

M[X²] = (M[X])² + D[X] = 200.

25. Стандартное нормальное (гауссовское) распределение: теорема Муавра-Лапласа, функция Лапласа и ее свойства, «закон трех сигм» для стандартной нормальной величины.

Пусть X ~ Bi(n,p). Тогда при n ® ¥ Р((Х_n – np)/(npq)^½ £ с) ® Ф(c), где Ф(с) – функция Лапласа.

В справочниках часто встречается также функция Лапласа Ф₀(x).

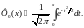
Ф(x) = ½ + Ф₀(x). Рассмотрим некоторые свойства функции Ф₀(x):

- Ф₀(-x) = -Ф₀(x).

- Ф₀(x) принимает значения от -½ до ½. Функция Ф(x) обладает всеми свойствами функции распределения, так как является функцией распределения стандартной нормальной случайной величины. Производная функции Ф((х-m)/s) является функцией плотности вероятности нормальной СВ.

. Для стандартной нормальной СВ m = 0, s = 1.

Параметр m равен МО нормальной СВ, а параметр s есть квадратный корень из значения дисперсии нормальной СВ.

Нормально распределенная СВ с большей вероятностью принимает значения, близкие к своему МО, что описывает «закон трех сигм». Неравенство Чебышева:

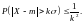
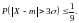
26. Нормальное (гауссовское) распределение. Функция Лапласа (интеграл вероятностей) и ее свойства. Плотность и функция распределения нормального распределения.

СВ X имеет нормальное (гауссовское) распределение с параметрами m и s² > 0, т.е. X ~ N(m, s²), если

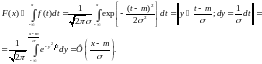
Функция Ф(x) называется функцией Лапласа.

В справочниках часто встречается также функция Лапласа Ф₀(x).

Ф(x) = ½ + Ф₀(x). Рассмотрим некоторые свойства функции Ф₀(x):

- Ф₀(-x) = -Ф₀(x).

- Ф₀(x) принимает значения от -½ до ½. Функция Ф(x) обладает всеми свойствами функции распределения.

Параметр m равен МО нормальной СВ, а параметр s есть квадратный корень из значения дисперсии нормальной СВ.

27. Случайные векторы. Закон распределения случайного вектора. Функция совместного распределения двух случайных величин. Таблица распределения. Плотность распределения. Связь функции распределения случайного вектора с его плотностью.

Двумерным случайным вектором (или двумерной СВ) Z = (по определению) col(X,Y) называется вектор, компонентами которого являются СВ X = X(w) и Y = Y(w), определенные на одном и том же пространстве W элементарных событий w. Функция F(x,y) = (по определению) Р({w: Х(w) £ х}{w: Y(w) £ у}) = (по определению) P{X £ x, Y £ y}, называется функцией распределения двумерной СВ Z = col(x,y). Двумерная СВ Z = col(x,y) называется дискретной, если СВ Х и Y дискретны. Простейшим способом задания закона распределения дискретной двумерной СВ является таблица распределения. Функция распределения имеет вид:

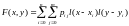
Где l – функция Хевисайда.

Неотрицательная кусочно-непрерывная функция f(x,y) называется плотностью распределения (плотностью вероятности) двумерной СВ Z = col(X,Y), если:

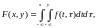
где используется символическая запись для двойного интеграла по области D = (по определению) {t £ x, t £ y}. Такая двумерная СВ называется непрерывной.