9. Нелинейные регрессионные модели и оценка их параметров.

Полиномиальные

Степенные

- многомерный случай

Гиперболические (обратная модель)

Экспоненциальные

Функция Гомперца

Показательные

где а - положительная константа

Логистические

Различают два класса нелинейных регрессионных моделей:

1. Нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам

Примером могут служить следующие модели: полиномиальная и гиперболическая (обратная модель)

2. Нелинейные как относительно включенных в анализ объясняющих переменных, так и по оцениваемым параметрам

Примером таких нелинейных моделей являются (например): степенная, показательная, экспоненциальная.

Для оценки параметров нелинейных моделей используют два подхода.

Первый подход основан на линеаризации модели.

Второй подход - нелинейная оптимизация на основе исходных переменных.

Линеаризация переменных - «замена переменных», логарифмирование обеих частей уравнения, комбинированный

10. Метод наименьших квадратов. Вывести выражение для мнк-оценки вектора b для линейной регрессионной модели.

Для нахождения оценок параметров уравнения регрессии чаще всего используется метод наименьших квадратов (МНК).

Обозначим оценки параметров уравнения регрессии β₀ и β₁ как b₀ и b₁.

В соответствии с методом наименьших квадратов (МНК) оценки b₀ и b₁ можно получить из условия минимизации суммы квадратов ошибок оценивания, т.е. минимизации суммы квадратов отклонений фактических значений зависимой переменной от расчетных ее значений, полученных на основе уравнения регрессии.

МНК:

y_i – фактические значения зависимой переменной,

ŷ_i - расчётные значения, полученные на основе уравнения регрессии.

Разность называется остатком и дает количественную оценку значения ошибки, т.е. показывает воздействие возмущающей переменной.

МНК позволяет получить несмещённые оценки, а в случае линейной модели – оценки с минимальной дисперсией, дающие хорошее приближение оценок b_j к истинным значениям коэффициентов регрессии β_j.

Для того, чтобы найти минимум функции Q, сначала рассчитывают частные производные первого порядка, затем каждую из них приравнивают к нулю и решают полученную систему уравнений.

=>

=>

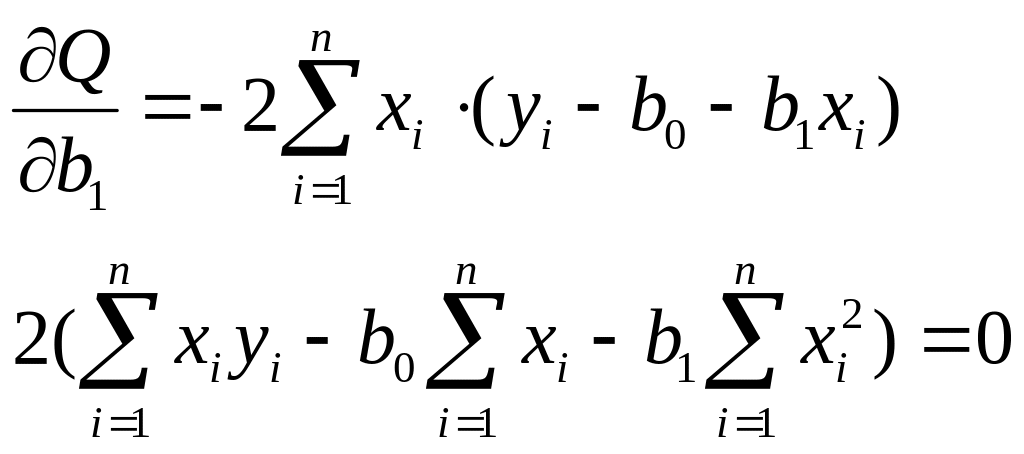Таким образом получают систему из двух линейных уравнений, которая называется системой нормальных уравнений:

Решим систему относительно b₀ и b₁.