1.3. Начисление простого процента и сложного процента.

Простой процент.

Простой процент начисляется за все время действия контракта на определенную первоначальную сумму. Этот способ начисления процентов называют “наращиванием без капитализации”. Наращенная сумма при ежегодном начислении процентов или будущая стоимость (future value) равна

, (1.8)

где r – годовая процентная ставка n – число лет.

Если начисление процента происходит ежедневно, то для простых процентов наращенная сумма рассчитывается по формуле

, (1.9)

где - временная база, или число дней в финансовом году³, Т – число дней наращения.

Процентный доход равен или .

Пример 4. Кредит в размере 2 млн. руб. был выдан на 60 дней под 12% годовых. Найти наращенную сумму и процентный доход.

Решение. По формуле (1.9) найдем наращенную сумму

2,4 млн. руб. Процентный доход равен =0,4 млн. руб.

Пример 5. Банк предлагает депозит с начислением на первоначальную сумму. Первые три месяца по ставке 4% годовых, в следующие три месяца процент возрастает на 0,5%. Найти наращенную сумму и процентный доход, если сумма вклада составляет 30 000руб.

Решение. Найдем процентный доход за первые три месяца =300 руб. Найдем процентный доход за следующие три месяца =337,5 руб. За все шесть месяцев процентный доход равен 300+337,5=637,5 руб. Наращенная сумма равна 30637,5 руб.

Сложный процент.

Начисление сложного процента осуществляется на наращенную сумму, поэтому этот способ начисления называют «наращением с капитализацией». Наращенная сумма при начислении сложного процента за произвольное число дней равна

, (1.10)

где r- годовая процентная ставка (per annual), выраженная в виде долей единицы. Величина часто бывает нецелым числом. В зависимости от внутренних правил банка для расчета наращенной суммы при дробном числе лет как формула (1.10) или применяться приближенная формула.

, (1.11)

где i- целая часть числа , а f - дробная часть этого числа. Если начисление сложных процентов происходит m раз в году течении n лет, то расчет наращенной суммы за время производят по формуле

, (1.12)

г де r – годовая процентная ставка (номинальная), – процентная ставка за период (periodic interest rate). Величина – называется множителем наращения, а – коэффициентом наращения. Наращенная сумма зависит от частоты начисления процентов. Чем больше частота начисления процентов, тем больше наращенная сумма. Таким образом, для вкладчика выгоднее частое начисление процентов, а для заемщика наоборот. В кредитных контрактах и депозитных договорах, когда начисление процентов происходит по сложной процентной ставке, указывается годовая процентная ставка, которая называется номинальной.

Рис.1.3. Наращенная сумма в зависимости от частоты начисления процентов

Рис.1.4. Наращенная сумма для простых и сложных процентов

Непрерывное начисление процентов.

Если частота начисления процентов становится непрерывной, то есть частота начисления процентов бесконечно возрастает , а временной интервал начисления становится бесконечно малым, то наращенная сумма или будущая стоимость рассчитывается по формуле

, (1.13)

где – число лет. При выводе (1.13) мы использовали известное приближение , где , при .

В практике кредитных расчетов непрерывное начисление процентов применяется редко. Обычно для кредитных расчетов применяется ежедневное начисление процентов. При непрерывном начислении процентов наращенная сумма рассчитывается по формуле

, (1.14)

где – сила роста, которая является фактически непрерывной процентной ставкой. Если сила роста постоянна, то наращенная сумма за время t равна

, (1.15)

При нестабильной экономике процентные ставки могут значительно изменяться в течение года. В этом случае наращенная сумма вычисляется по формуле

, (1.16)

где – последовательные значения процентных ставок в соответствующие периоды.

Если необходимо найти количество лет для увеличения начальной суммы в N раз, то для простых процентов имеем из формулы (1.8)

; (1.17)

для сложных процентов из формулы (1.12)

, (1.18)

. (1.19)

Пример 6. Сколько лет потребуется для увеличения первоначальной суммы в 1,2 раза, если номинальная процентная ставка равна 9%, а начисление процентов происходит 4 раза в год.

Решение. По формуле (1.19) найдем необходимое число лет:

N = 1,2; m = 4, 2 года.

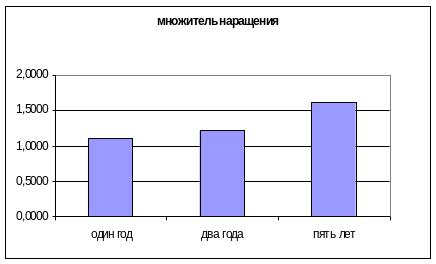
Пример 7. Рассчитать накопленную сумму для различных вариантов начисления процентов за один год, два года, 5 лет. Начальная сумма равна 1000 руб., годовая процентная ставка равна 10%.

Решение. Расчет проведем по формуле (1.12) в Excel. Результаты расчетов приведены ниже в таблице и на гистограммах ниже.

Таблица 1. Наращенные суммы и множители наращения для различной частоты начисления процентов в году.

	сумма	Частота начислений в году	Наращенная сумма	Базисное наращение	Цепное наращение
		m
	Начальная сумма 1000	1	1100	100
		2	1102,5	102,5	2,5
		4	1103,813	103,813	1,313
		6	1104,260	104,260	0,448
		12	1104,713	104,713	0,453
		360	1105,171	105,171	0,458

частота начисления %	m	Множитель наращения
		один год	два года	пять лет
раз в год	1	1,1	1,21	1,61051
два раза в год	2	1,1025	1,2155	1,6289
раз в квартал	4	1,1038	1,2184	1,6386
ежемесячно	12	1,1047	1,2204	1,6453
ежедневно	365	1,1052	1,2214	1,6486
непрерывное		1,1052	1,2214	1,6487

Рис. 1.5. Зависимость наращенной суммы и величины множителя наращения от частоты начисления процентов.

Эффективная процентная ставка.

Эффективная процентная ставка позволяет сравнить доходности различных финансовых операций или, другими словами, сравнить различные методы получения процентного дохода.

В финансовых расчетах при анализе доходности финансовых операций часто приходится сравнивать различные виды процентных ставок, в которых выражается доходность данной конкретной финансовой операции. Например, банки предоставляют различные виды депозита с различными сроками, частотой начисления процентного дохода, различными номинальными ставками. Какой вариант выбрать? Или, например, другая задача. Вы хотите инвестировать 10000 руб. Возможны несколько вариантов: положить на депозит, купить облигации или купить акции. Эти финансовые операции также характеризуются величиной процентной ставки. Для сравнения результатов финансовых операций обычно применятся эффективная процентная ставка.

Эффективной процентной ставкой называется годичная ставка сложных процентов, дающая тот же финансовый результат: соотношение между полученной суммой за время t = T и затраченной суммой , которая получается при любой схеме выплат.

, (1.20)

, (1.21)

где Т измеряется в годах. Эффективная процентная ставка, как видно из формулы (1.21), зависит от отношения конечной и начальной сумм и от продолжительности периода начисления процентов .

Если проценты начисляются m раз в год по схеме сложных процентов, то формула (1.20) приобретает более простой вид. Действительно, из формулы (1.12), учитывая, что Т = n получим

. (1.22)

Эффективная процентная ставка позволяет сравнить доходности различных финансовых операций или, другими словами, сравнить различные методы получения процентного дохода.

Пример 8. Найти эффективную процентную ставку при ежеквартальном начислении сложных процентов. Номинальная (годовая) процентная ставка равна 18%.

Решение. r = 0,18; m = 4, , .

Сравним наращенные суммы при начислении по эффективной процентной ставке и номинальной. Пусть первоначальная сумма вклада равна 400 тыс. руб., процентная ставка равна 19,25%, срок вклада 2 года. Наращенная сумма равна

тыс. руб.

Пусть теперь та же сумма 400 тыс. руб. вносится на два года под 18% годовых с ежеквартальным начислением процентов. Наращенная сумма в этом случае равна

тыс. руб.

Наращенные суммы равны. Это означает, что наращение по эффективной процентной ставке дает тот же финансовый результат, что и наращение при ежеквартальном начислении сложных процентов по номинальной процентной ставке.

Пример 9. Предприниматель может получить ссуду: а) на условиях ежеквартального начисления сложных процентов из расчета 75% годовых, б) на условиях полугодового начисления сложных процентов из расчета 80% годовых. Какой вариант предпочесть?

Решение. Задачу можно решить двумя способами: 1) сравнить наращенные суммы, 2) сравнить эффективные процентные ставки.