Тема 9 Правила принятия решений при различении сигнала.

Задачи при приеме сигналов

В зависимости от вида и назначения СПД при приеме сигналов возникают следующие 3 задачи:

1. Обнаружение

2. Различение

3. Восстановление сигналов

При обнаружении сигналов задача сводится к ответу на вопрос: имеется ли на входе приемника сигнал и шум или только шум? С такой задачей обычно встречаются в радиолокации. Кроме того, эта задача имеет место и в системах связи, в которых отсутствие сигнала является признаком передачи информации, например, 1 передается сигналом, 0 – его отсутствием (так называемый системы с пассивной паузой).

При передаче 2-х сигналов А1 и А2 возникает задача не обнаружения, а различения этих сигналов. Очевидно, нужно стремится к тому, чтобы различия были наибольшими и максимально стойкими к воздействию помех. При этом СПД необходимо строить таким образом, чтобы различия между сигналами было максимальным и как можно более стойким к воздействию помех. Передача данных, при которой каждому символу соответствует сигнал, не равный нулю, называется передачей с активной паузой.

Задача восстановления сигналов состоит в том, чтобы получить выходной сигнал наименее отличающимся от входного.

Различение сигналов как статическая задача.

Пусть область Х принимаемых сигналов разбита на неперекрывающиеся области Х_j (j=1…m), при чем каждому элементарному сигналу А_i соответствует область Х_і (А_i →X_i). Если принятый сигнал попал в область Х_i то приемник принимает решение о том, что передавался сигнал А_i.

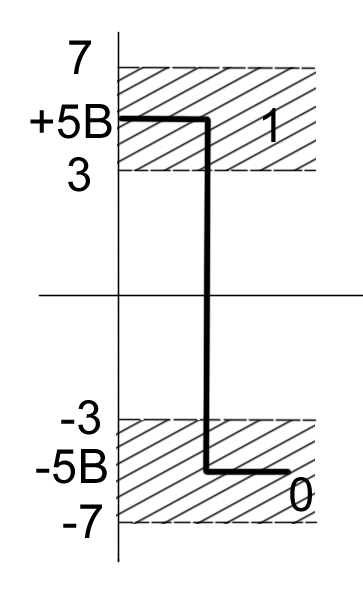
С некоторой вероятностью принятый сигнал может попасть в любую из областей, что приведет к тому, что будет принято ошибочное решение о том, что передавался сигнал Aj

Вероятность того, что переданный элемент принят правильно, обозначим

p(X_i /A_i),

а вероятность того, что он будет принят ошибочно, равна .

Условная вероятность p(X_i /A_j) зависит от способа модуляции, помех, решающей схемы приемника и др.

Полная вероятность ошибочного приема равна

,

где р(А_і)- априорная вероятность появления передаваемых символов.

Если в канале связи отсутствуют помехи, то

р(Х_і/А_j)=1 для і=j.

р(Х_і/А_j)=0 для і≠j.

Если в канале алфавит на входе и выходе совпадают и для любой пары символов вероятности перехода равны p_ji=p(A_j/A_i)=p₀, то такой канал называют симметричным.

Тема 9 Критерий оптимального приема сигналов.

Пусть на входе приемника поступает сумма сигнала и помехи

X(t)=A(t)+N(t),

где N(t) – аддитивная помеха с известным законом распределения.

На основании сигнала X(t) приемник воспроизводит сигнал A_i. При наличии помех это воспроизведение может быть неточным.

По принятой реализации сигнала X(t) приемник вычисляет апостериорное распределение p(A_i/X).

При передаче дискретных сообщений широко используется критерий Котельникова. Согласно этому критерию, принимается решение, что передавался такой сигнал А_і, для которого апостериорная вероятность р(А_і/Х) имеет максимальное значение. То есть регестрируется сигнал А_і, если выполняется следующее неравенство:

p(A_i/X)>p(A_j/X) Ѵ i≠j (для любого i≠j)

На основании формулы Байеса

переписываем неравенство:

P (A_i)*p(X/A_i)>p(A_j)*p(X/A_j),

Если передаваемые сигналы равновероятные - правило принятия решения принимает такой вид.

Оптимальный прием дискретных сигналов при влиянии помехи «белый шум».

Помеха имеет равномерный спектр мощности с интенсивностью δ²

Т.к. сигналы A_i(t), X(t) и помеха N(t) заданы на конечном интервале (0<t<T), их можно представить в виде разложенной по ортогональным функциям:

Где x_e= a_ie+n_e;

Т.к. помеха «белый шум» имеет нормальное распределение, то и коэффициенты Фурье n_e

Будут иметь нормальное распределение с той же дисперсией (δ²) и средним значением равным 0.

Коэффициенты Х_е так же имеют нормальное распределение с той же дисперсией δ² и средним значением, равным a_ie:

Т.к. коэффициент n_e независимый, коэффициенты х_е также будут независимыми. Тогда многомерное распределение коэффициентов х_е, т.е. условное распределение р(Х/А_і) будет равно произведению одномерных распределений, т.е.

=

Подставляя это выражение в формулу критерия Котельникова, получим:

Прологарифмировав, получим:

Т.к. , после возведения в квадрат и усреднения по времени, получим:

Тогда условие оптимального приема можно записать в виде:

Type equation here.

В случае, если априорные вероятности сигналов одинаковые p(A₁)=p(A₂)=…=p(A_m)=1/m, критерий Котельникова принимает более простой вид:

Отсюда следует, что при равновероятных сигналах оптимальный приемник воспроизводит сообщение, соответствующее тому переданному сигналу, который имеет наименьшее среднеквадратичное отклонение от принятого сигнала.

Последнее неравенство можно записать в другом виде, раскрыв скобки:

Для сигналов, энергии которых одинаковы,

, это неравенство переходит в следующее выражение:

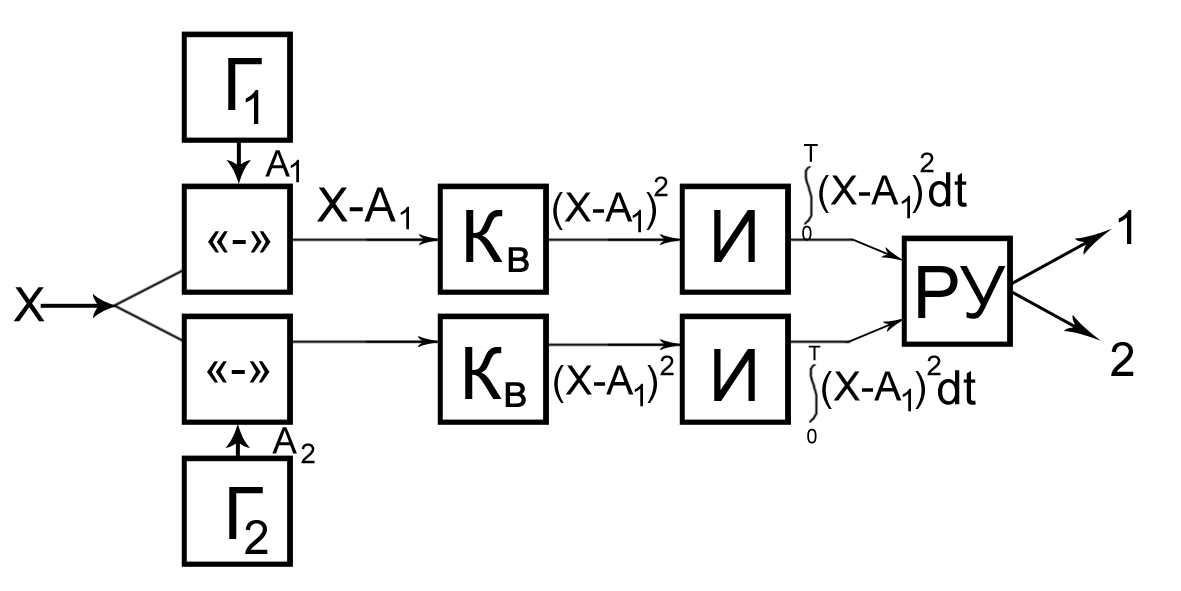
И схема приемника примет следующий вид:

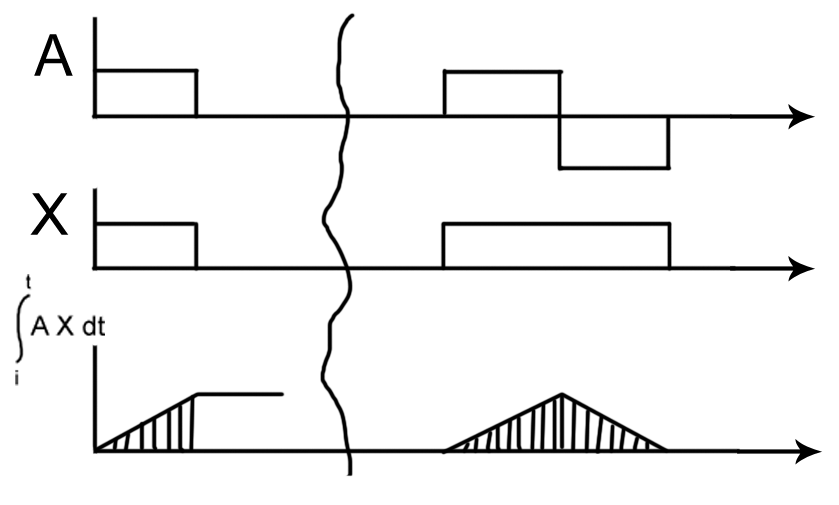
Интеграл от произведения 2^х функций времени, называется корреляционным интегралом