11.3. Расчет эффективности эмиттера

Воспользуемся полученным в 11.2 соотношением для

.

Поскольку транзистор диффузионный, для плотности дырочного тока можно записать

.

После интегрирования получим

. (11.1)

Ось направлена слева направо, точка означает границу пе­рехода Э – Б.

Но

, (11.2)

где – равновесная концентрация дырок в n-области; – напря­жение в эмиттере.

В области коллектора имеем ( )

,

где – ширина области базы; – напряжение в коллекторе. Подставим эти величины в (11.1):

, (11.3)

откуда

. (11.4)

Так как коллекторное напряжение порядка 10 В, а величина при комнатной температуре равна 0,025 эВ, то .

Тогда

. (11.5)

Электронная составляющая тока эмиттера

. (11.6)

Учитывая, что , , поэтому можно пренебречь единицей и записать:

.

Таким образом, эффективность эмиттера составит

. (11.7)

Между коэффициентами диффузии носителей и , и подвижностями и существуют так называемые соотношения Эйнштейна будут получены позже):

; .

Подставив эти соотношения в (11.7) и произведя преобразование , получим

.

Выражение для примет вид

,

и, воспользовавшись тем, что и , получим оконча­тельное выражение для эффективности эмиттера:

.

11.4. Расчет эффективности переноса

Для расчета эффективности переноса дырок через область базы воспользуемся соотношением

.

Выражение для плотности дырочного тока эмиттера – формула (11.5). Найдем рекомбинационную составляющую тока . При расче­те следует учитывать, что рекомбинация происходит как в объеме базы (эту составляющую обозначим через ), так и на ее поверхности (обозначим через ). Полная эффективность переноса, естественно, будет равна произведению . Для определения эффективности пе­реноса, связанной с рекомбинацией в объеме воспользуемся урав­нением непрерывности

(11.8)

(рекомбинация в объеме тем больше, чем меньше время жизни дырок и чем больше превышение неравновесной концентрации дырок над равновесной концентрацией дырок в объеме базы ).

Уравнение (11.8) легко интегрируется:

.

Выражение для было также получено в предыдущем парагра­фе (см. формулы (11.1) и (11.2)):

.

С помощью этих соотношений легко получить окончательное вы­ражение для j_r:

.

Эффективность переноса, связанная с рекомбинацией в объеме , составляет

.

Для определения эффективности переноса, связанной с рекомби­нацией на поверхности , необходимо воспользоваться реальной моделью транзистора (рис. 11.6). В производстве в тонкую n-область базы вплавляется индий. При этом образуются два p-n-перехода – Э – Б и Б – К. Омический вывод в виде области базы выполняется в виде кольца у края базы. Вся конструкция осесимметрична.

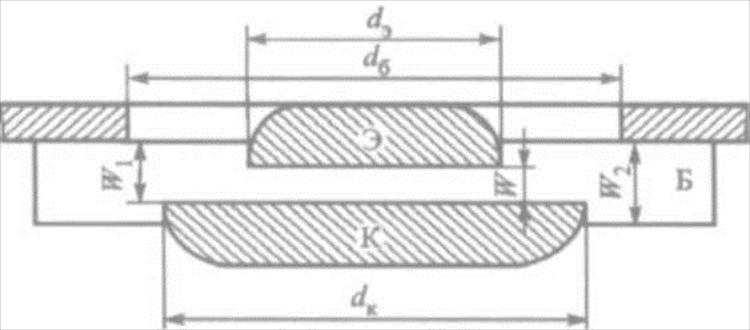
Рис. 11.6. Реальная модель транзистора

Коллектор имеет диаметр несколько больший, чем диаметр эмиттера, чтобы перехватывать возможно большее число инжектированных из эмиттера дырок. За эффективную поверхность рекомбинации принимаются площадь кольца с внутренним диаметром, равным диаметру эмитте­ра, и шириной, равной ширине базы . Пути рекомбинирующих на поверхности дырок показаны на рис. 11.5.

При этих условиях эффективная поверхность рекомбинации со­ставит

,

а часть тока, теряемая вследствие поверхностной рекомбинации,

,

где – скорость поверхностной рекомбинации; .

Выразим через дырочный ток эмиттера:

или

.

Эффективность переноса, связанная с рекомбинацией на поверх­ности есть, очевидно,

.

Полная эффективность переноса

.

И, наконец, коэффициент передачи транзистора по току

.

Из этой формулы видно, что для того чтобы а было близко к еди­нице, необходимо выполнение следующих условий: ширина области базы должна быть существенно меньше диффузионных длин и ; проводимость базы должна быть много меньше проводимости эмиттера ; скорость поверхностной рекомбинации должна быть возможно меньшей, что достигается травлением поверхности с по­следующей промывкой ее деионизованной водой.