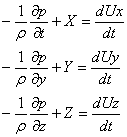1.Дифференциальное уравнение равновесия жидкости (уравнения Эйлера)

Система уравнений Эйлера (уравнения равновесия) определяет закон распределения давления в покоящейся жидкости вдоль соответствующей оси координат.

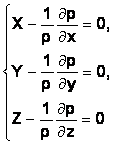
здесь X,Y,Z – напряжения массовых сил в проекциях на соответствующие оси координат x, y, z,

p – давление в соответствующей точке жидкости,

ρ - плотность жидкости.

Из уравнений Эйлера можно получить следующий вид основного дифференциального уравнения равновесия жидкости

Если ввести силовую (потенциальную) функцию U, такую, что

,

,

,

то для несжимаемой жидкости дифференциальное уравнение равновесия примет вид:

Основное уравнение гидростатики

В однородном поле силы тяжести при постоянстве плотности жидкости

dU=gdz,

тогда

dp= – ρgdz,

Проинтегрировав, получим основное уравнение гидростатики:

p=p₀+ρgh,

h=(z₀-z)  - расстояние по вертикали между рассматриваемыми двумя точками (нулевой и точкой, в которой определяется давление).

2.Ур-е неразрывности потока = ур-е постоянства расхода.

Выделим бесконечно малый объем жидкости  , масса которого  , и применим к нему закон сохранения массы

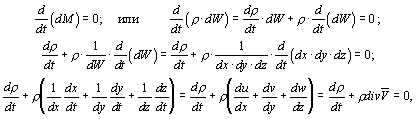
где   - проекции вектора скорости   на оси координат.

Раскрыв в последнем уравнении полную производную плотности по времени, получим окончательный результат

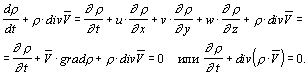       (1.2.1)

Для несжимаемой жидкости, плотность которой не изменяется, т.е.  , уравнение неразрывности примет вид:

.                                  (1.2.2)

Проанализируем установившийся, т.е. не изменяющийся с течением времени, поток жидкости. В каждой точке такого потока вектор скорости не будет меняться с течением времени. Для анализа полезно ввести линии в области течения, касательные к вектору скорости в каждой точке потока. Такие линии называют линиями тока.

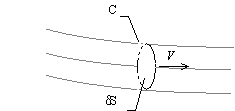
Рассмотрим замкнутую кривую (контур) С, проведенную вокруг точки в потоке жидкости и охватывающую элементарную площадку S, которая расположена в плоскости, перпендикулярной вектору скорости рассматриваемой точки. Линии тока, проходящие через контур, образуют трубку тока, как показано на рисунке.

Поскольку, по определению, не существует компоненты вектора скорости, нормальной к линиям тока, ни одна частица жидкости не пересечет поверхность трубки тока. Следовательно, массовый расход жидкости вдоль трубки тока остается постоянным, т.е.

,

где  - плотность жидкости; V- скорость жидкости вдоль трубки тока.

Так как для капельных жидкостей  практически остается постоянной, то остается постоянным и объемный расход жидкости Q вдоль трубки тока

.

Полный объемный расход через всю площадь течения S, в пределах которой скорость u остается постоянной равен

.                                  (1.2.3)

Уравнения (1.2.1), (1.2.2) и (1.2.3) представляют собой различные формы записи уравнения неразрывности.

оно является первым основным уравнением гидродинамики. Из него следует, что средние скорости обратно пропорциональны площадям соответствующих живых сечений потока.

3.Уравнение движения идеальной жидкости Эйлера

Уравнение Эйлера которое выражают условия равновесия жидкости

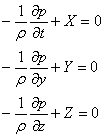                            (4.1)

Чтобы получить уравнения движения воспользуемся принципом Даламбера для перехода от равновесия к движению необходимо к действующим силам прибавить силы инерции.

С учетом того, что уравнение (4.1) приведено к единицы массы, соответствующие силы инерции будут:

;  ; 

Прибавляя силы инерции, действующие силы к силам получим: