Сложение погрешностей

1)Сложение систематических погрешностей.

∆сист.=1.1=1.1

P=0.95- равномерное распределение

Иногда так: ∆сист.=+-шире, т.к. складываются ±,т.е. погрешность уходит либо только в «+», либо в «-»

2.Сложение случайных погрешностей

∆случ.=P=0.95

ГОСТ-сложение погрешностей

1)если< 0.8

∆=∆случ.=t*S(Ᾱ) пренебр. сист. погрешностью

2)если>8

∆=∆сист. Пренебрегаем случайной погрешностью

3)промежуточные случаи

0.85 S(Ᾱ) < ∆сист. < 8S(Ᾱ)

∆=k*– суммарная СКП

K=

=

Рекомендации по повышению точности измерений

Суммарная погрешность состоит из двух составляющих:

-систематическая

-случайная

1)если ∆сист. >>∆случ. –выбираем другой прибор

2)если ∆сист. <<∆случ.- увеличиваем количество измерений

3)если ∆сист. ≈∆случ. – и то, и то

Запись окончательного результата:

Указывает Ᾱ , суммарная погрешность ±∆(систематическая + случайная),

вероятность

Ᾱ±∆, Р=…

U=23±2 В Р=0.95

Правила округления:

1)Округление производится в окончательном результате

2)Рассчитывается погрешность измерений и округляется до 1 значащей цифры. Если первая 1 или 2, то указывается 2 числа.

3)Результат измерения округляется в соответствии с его погрешностью.

Алгоритм обработки результатов многократных измерений.

Измерения бывают :

-равноточные

-неравноточные

Равноточные измерения.

Эти измерения проводятся одним наблюдателем в одинаковых условиях с помощью одного и того же средства измерений.

Алгоритм обработки равноточных измерений:

1.В таблицу записываем результаты наблюдений.

2.Исключаем известные систематические погрешности.

3.Вычисляем среднее арифметическое, которое считается результатом измерений(действительное и истинное).

4.Вычисляем и записываем в таблицу отклонение от среднего и его квадрат

=;

5.Вычисляем СКП среднего арифметического

6.Задаем значение доверительной вероятности.

7.Определяем по таблице коэффициент Стьюдента.

8.Определяем погрешность измерений ( доверительный интервал)

9.Находим суммарную погрешность(∆случ. и ∆сист.)

10.Записываем окончательный результат

Ᾱ±∆, Р=…

Неравноточные измерения.

Это измерения одного и того же значения величины, проводимое разными наблюдателями, различными средствами и в различных условиях.

5 стендов

S()	S()	S()	S()	S()

Результатом измерений является средневзвешенное значение с учетом всех средних значений и их весовых коэффициентов(не среднее арифметическое!)

=

Каждое входит в результат с учетом коэффициента доверия.

=*+*+…+*==

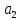СКП: S(=

=*S(

Результат неравноточных измерений:

±,Р=0.95

Интервалы перекрываются и интервал меньше.

Погрешность косвенных измерений.

A=f(,

Измерено ±∆;±∆

Абсолютная погрешность:

∆А=

Ᾱ=f(,…,)

Относительная погрешность:

δ=

СКП: S(Ᾱ)=

Проверка гипотезы нормального распределения.

Из гистограммы ,S=– подставляем в функцию нормального распределения.

Два критерия оценки вида распределения:

1)Критерий Пирсона (χ²)

2)Составной критерий

Для проверки гипотезы распределения сравнивают экспериментальную гистограмму с расчетным распределением на основе СКП и .

Критерий χ²

1)Вычисляем χ²=

- экспериментальное значение

- теоретическое значение

Задача:

Погрешность измерения тока распределена равномерно в интервале мА. Определить систематическую погрешность 1)∆ сист.,2)СКПS, 3) вероятность того, что исправленный результат отличается от истинного на 1 мА

f(∆)

-1 0 3 i,мА

Нормировка

f(∆)=

∆сист.= ==1 мА

Исправленный результат с учетом систематической погрешности :

f(∆)

0.25

-2 -1 0 1 2 i,мА

Вероятность того, что исправленный результат находится в интервале ±1 мА:

СКП S===1.16 мА

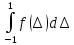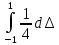P=== 0.5- 50%.