
Метрология / Шпоры метрология 31-35
.docx|
31. Нормальный закон распределения погрешностей. 31. Нормальный закон распределения погрешностей. Законы распределения вероятностей: 1)Нормальное распределение (з-н Гаусса) 2)Равномерное (однородное) 3)Треугольное 4)Арксинусное Числовыми характеристиками являются: а)Математическое
ожидание m= б)Дисперсия
D(∆)= в)Среднеквадратичная
погрешность σ(∆)= Интеграл вероятности (интеграл Лапласса)-используется для расчета вероятности: Ф(z)= Ф(z)-из таблицы для разл. z Нормальное распределение (закон Гаусса): P(∆x)= S=σ- СКП ∆x=x-Ᾱ=x-m=∆-∆ср. S= ( Разброс случ значений характеризует СКП. |
32. Алгоритм обработки равноточных измерений. Измерения бывают : -равноточные -неравноточные Равноточные измерения. Эти измерения проводятся одним наблюдателем в одинаковых условиях с помощью одного и того же средства измерений. Алгоритм обработки равноточных измерений: 1.В таблицу записываем результаты наблюдений. 2.Исключаем известные систематические погрешности. 3.Вычисляем среднее арифметическое, которое считается результатом измерений(действительное и истинное). 4.Вычисляем и записываем в таблицу отклонение от среднего и его квадрат
5.Вычисляем СКП среднего арифметического 6.Задаем значение доверительной вероятности. 7.Определяем по таблице коэффициент Стьюдента. 8.Определяем погрешность измерений ( доверительный интервал) 9.Находим суммарную погрешность(∆случ. и ∆сист.) 10. Записываем окончательный результат Ᾱ±∆, Р=… |
33. Алгоритм обработки неравноточных измерений. Это измерения одного и того же значения величины, проводимое разными наблюдателями, различными средствами и в различных условиях. 5 стендов Результатом
измерений является средневзвешенное
значение с учетом всех средних значений
и их весовых коэффициентов(не среднее
арифметическое!)
Каждое
=
СКП:
S(
Результат неравноточных измерений:
Интервалы
перекрываются и интервал
|
|
34. Расчет погрешностей косвенных измерений. A=f( Измерено
Абсолютная погрешность: ∆А= Ᾱ=f( Относительная погрешность: δ= СКП:
S(Ᾱ)=
|
35. Суммирование случайных и систематических погрешностей. 1)Сложение систематических погрешностей. ∆сист.=1.1 Иногда
так: ∆сист.= 2.Сложение случайных погрешностей ∆случ.= ГОСТ-сложение погрешностей 1)если
∆=∆случ.=t*S(Ᾱ) пренебр. сист. погрешностью 2)если
∆=∆сист. Пренебрегаем случайной погрешностью 3)промежуточные случаи 0.85 S(Ᾱ) < ∆сист. < 8 S(Ᾱ) ∆=k* K=
|
|
|
|
|
|
|
33. |
32. |
31. СКП применяют: 1)Для сравнения точности измерений, выполненных различными методами 2)Значение
СКП показывает ширину интервала, в
котором истинное значение находится
с вероятностью 0,68 A±S→P=0.68 A±2S→P=0.954 A±3S→P=0.997
СКП среднего арифметического значения: S(Ᾱ)= СКП среднего арифметического используется для расчета случайной погрешности при заданной доверительной вероятности. Для
N
измерений ∆случ.=± Свойства
действительного значения Ᾱ и случайных
отклонений ∆ 1)
2)Сумма квадратов отклонений от среднего арифметического имеет наименьшее значение
|
|
|
35. |
34.
|
|
|
|
|



 (СКП,СКО)
(СКП,СКО) Z=
Z=

 -СКП
-СКП -Ᾱ)
-отклонение от среднего
-Ᾱ)
-отклонение от среднего =
= ;
;

 =
=
 входит в результат с учетом коэффициента
доверия.
входит в результат с учетом коэффициента
доверия. =
= *
* +
+ *
*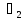 +…+
+…+ *
* =
=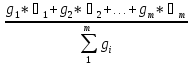

 =
=

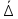 =
= *
S(
*
S(
 ±
± ,Р=0.95
,Р=0.95 меньше
меньше
 .
. ,
,
 ±∆
±∆ ;
;
 ±∆
±∆
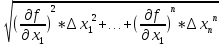
 ,…,
,…, )
)

 =1.1
=1.1 P=0.95
раномерное распределение
P=0.95
раномерное распределение +
+ -шире, т.к. складываются ±,т.е.
погрешность уходит либо только в «+»,
либо в «-»
-шире, т.к. складываются ±,т.е.
погрешность уходит либо только в «+»,
либо в «-» P=0.95
P=0.95 <
0.8
<
0.8 >8
>8 – суммарная СКП
– суммарная СКП
 =
=



 =
=
 *S(Ᾱ),
*S(Ᾱ),
 -
коэффициент Стьюдента(зависит от
числа измерений и доверительной
вероятности)
-
коэффициент Стьюдента(зависит от
числа измерений и доверительной
вероятности) =
=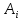 -Ᾱ:
-Ᾱ: имеет
разные знаки, след-но Σ
имеет
разные знаки, след-но Σ =0
=0 =
= -min
-min