5. Исследование цифровой системы на устойчивость.
Как
известно, непрерывная система
устойчива, если все корни ее
характеристического уравнения лежат
в левой полуплоскости. При исследовании
дискретных систем вместо р используется
новая переменная z =
.
Конформное преобразование z =
отображает
левую полуплоскость плоскости р в
область, ограниченную окружностью
единичного радиуса на плоскости z, при
этом мнимая ось отражается в саму эту
окружность [1]. Следовательно, для того
чтобы системы была устойчива необходимо
и достаточно, чтобы корни
характеристического уравнения лежали
внутри единичной окружности.
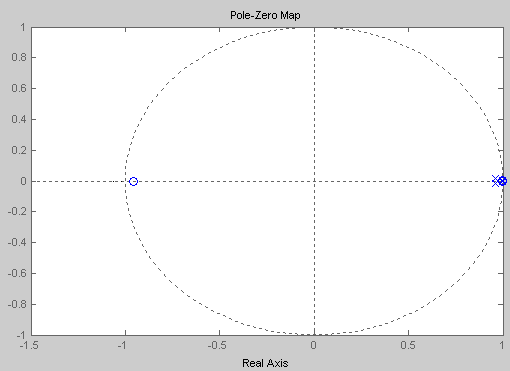
Рис. 23. Проверка устойчивости ЦСАУ
Как видно из рис. 23, все корни характеристического уравнения лежат внутри единичной окружности, следовательно, проектируемая цифровая система устойчива.
Заключение
В данной работе была спроектирована модель лапы шагающего робота. Для этого был проведен анализ существующих конструкций, выявлены их недостатки, предложена новая конструкция шагающего робота.
В данной работе разработан привод лапы шагающего робота. Составлена его кинематическая схема, произведено моделирование в программном продукте Mathlab 2000.