45. Вращение системы отсчета

4.1.1Углы Эйлера

Часто вместо трех независимых направляющих косинусов используют три угла Эйлера, которые вводятся следующим образом.

46. Углы Эйлера

Этот вывод полностью относится к определению положения твердого тела, в чем легко убедиться, жестко скрепляя «штрихованную» систему отсчета с данным твердым телом. (Конец задания 17 Горвиц, стр. 152)

4.1.2Простейший случай, когда ориентация системы определяется одним углом (начало задания 18, стр. 152)

47. Реализация поворота системы координат на произвольный угол с помощью углов Эйлера

Транспонированную матрицу обозначают символом . Таким образом, для

ортогональной матрицы A имеем .

4.2Поступательное движение и изменение ориентации системы отсчета

4.2.1Поступательное движение системы отсчета

В случае поступательного движения ориентация системы S' относительно

48. Поступательное движение тела

4.2.2Изменение ориентации при неизменном положении начала системы S'

49. К доказательству теоремы Эйлера

4.2.3Повороты твердой квадратной пластинки

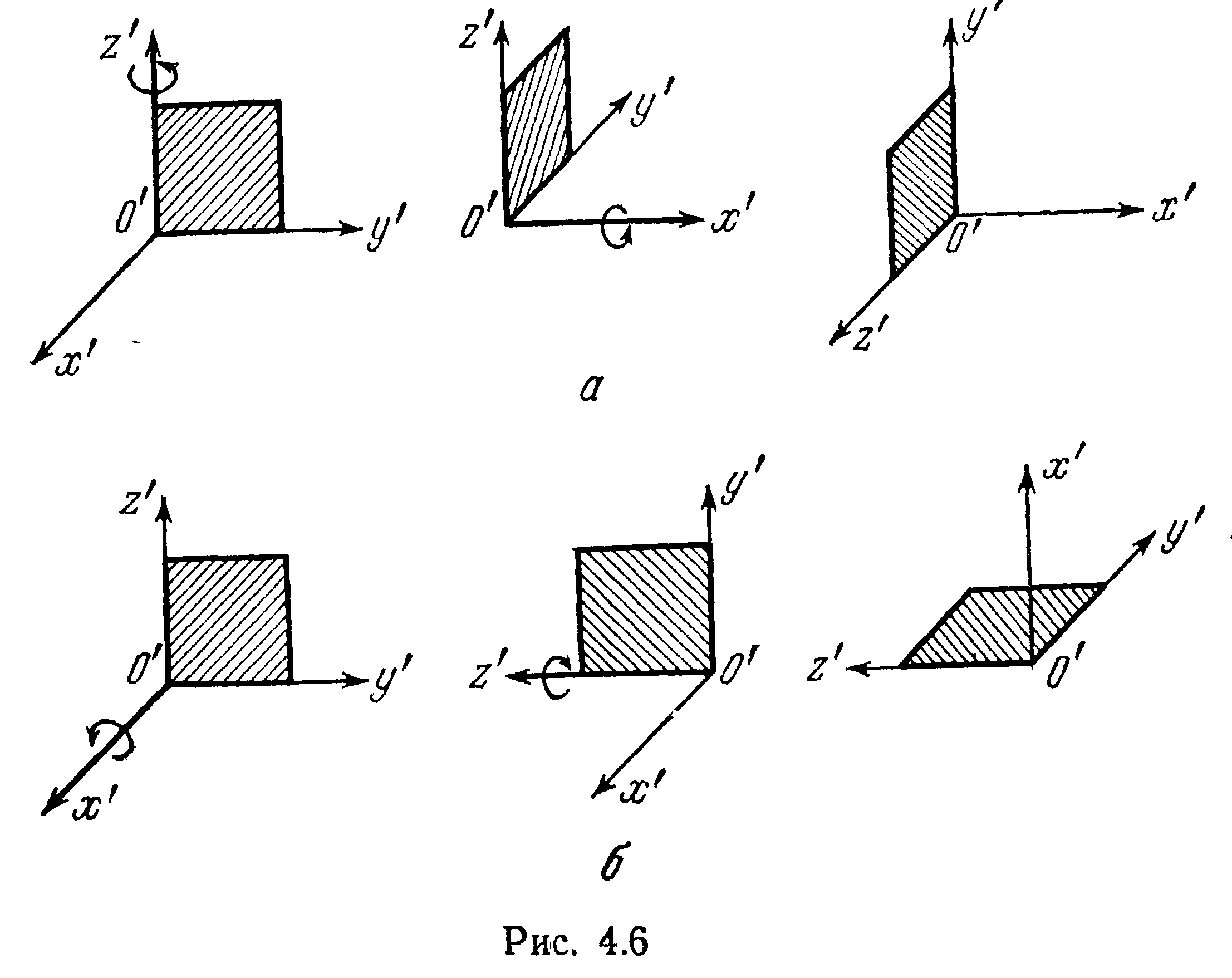
50. Повороты твердой квадратной пластинки

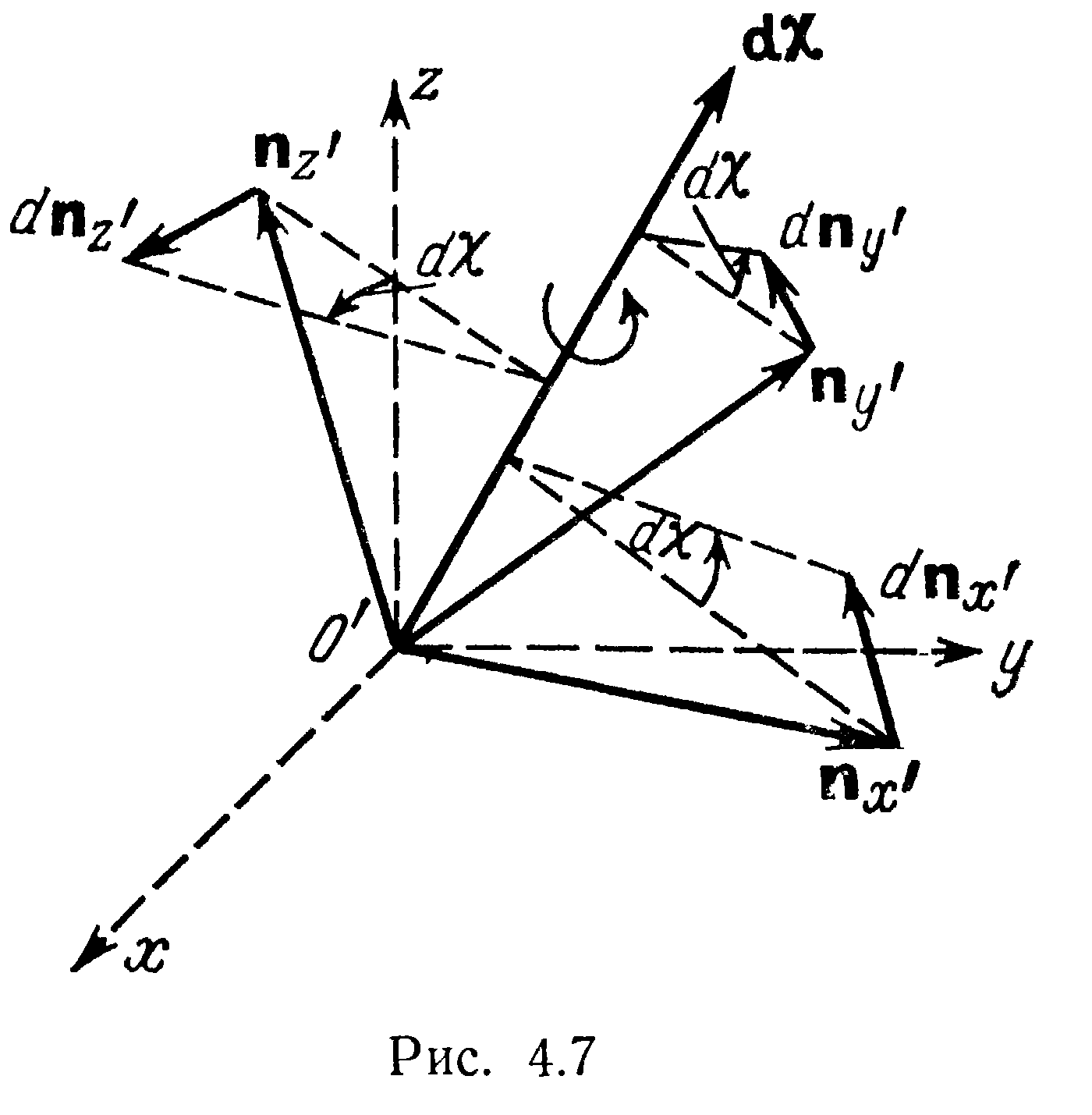
51. Приращение базисных векторов

4.2.4Угловая скорость

52. Приращение при повороте

(Конец задания 18, стр. 161)

4.2.5Пример 4.1. Регулярная прецессия твердого тела (начало задания 19, стр. 161)

Углы Эйлера,

53. Изменение ориентации системы отсчета

4.3Общий случай движения системы отсчета

54. Перемещение системы из положения 1 в положение 2

55. Пример квадратной пластинки

4.4Положение, скорость и ускорение материальной точки относительно разных систем отсчета

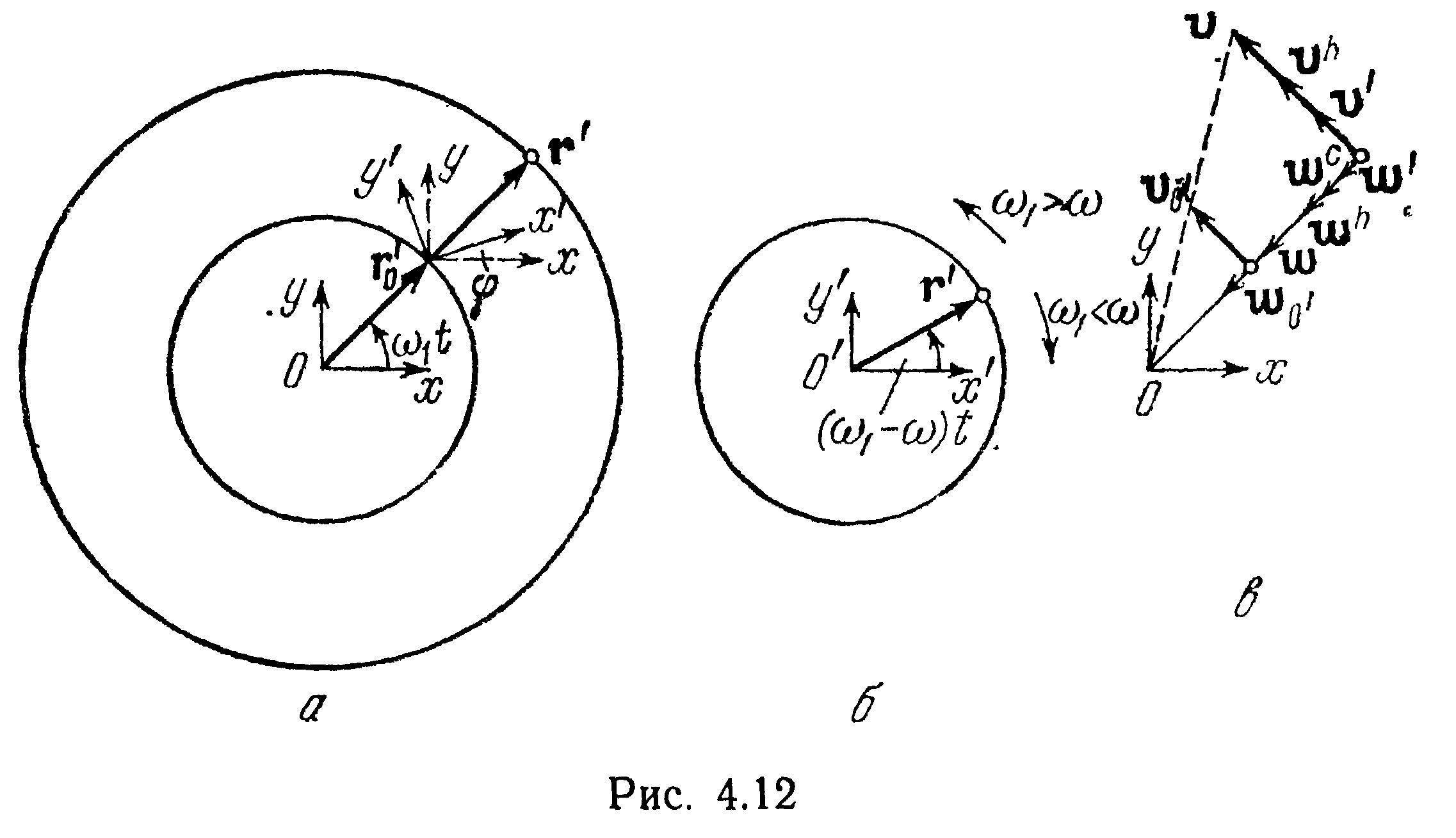
56. Движение точки относительно системы S', если начало О' этой системы движется по окружности

(Конец задания 19, стр. 171)

4.5Уравнение движения материальной точки относительно неинерциальной системы отсчета; силы инерции (начало задания 20, стр. 171)

4.5.1Пример 4.3. Уравнение движения точки относительно Земли

57. Угол между экваториальной плоскостью и направлением от центра Земли

4.5.2Пример 4.4. Отклонение падающего (или взлетающего) тела от вертикали

58. Траектории точки и направления сил инерции

4.5.3Пример 4.5. Состояние невесомости

(Конец задания 20, стр. 171)

4.6Законы изменения кинетического момента и кинетической энергии относительно поступательно движущейся системы центра масс

1 * Утверждения (1.5) и (1.7) по существу использовались Ньютоном. Однако Ньютон возвел их в абсолютные постулаты и тем самым пришел к представлениям о времени и пространстве как о «пустых» вместилищах тел и событий. Ньютон писал: «Длительность или продолжительность существования вещей одна и та же, быстры ли движения (по которым измеряется время), медленны ли, или их совсем нет ...» и «Как неизменен порядок частей времени, так неизменен и порядок частей пространства» [3].