2.4.2Пример 2.4. Движение по баллистической траектории

Пусть достаточно малое тело массы m запускается с поверхности Земли со скоростью Пренебрегая сопротивлением атмосферы, определить максимальную высоту, дальность и время полета тела (под дальностью будем понимать длину дуги большого круга, которая по поверхности Земли соединяет точки вылета и падения,— см. рис. 2.8).

Этот пример является частным случаем примера 2.3, поэтому выбор системы координат и предыдущие результаты остаются в силе. В частности, в рассматриваемом примере тело будет двигаться по отрезку эллиптической орбиты, пересекающей поверхность Земли ,в точках вылета и падения.

Максимальная высота подъема тела над поверхностью Земли равна

,

где r определяется одной из формул (2.73), а значения параметра и эксцентриситета орбиты находятся с помощью формулы (4) примера 2.3:

,

.

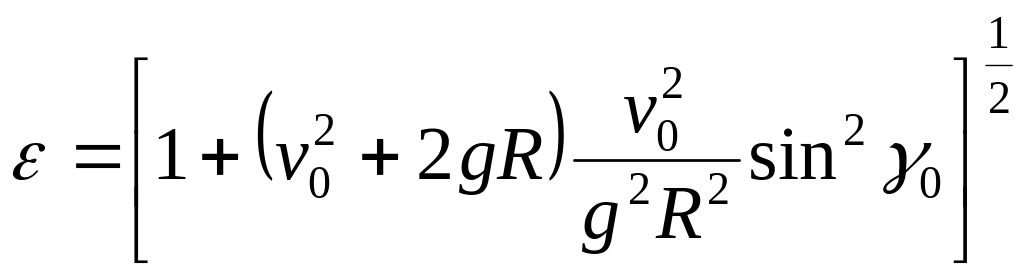Используя эти соотношения, получим

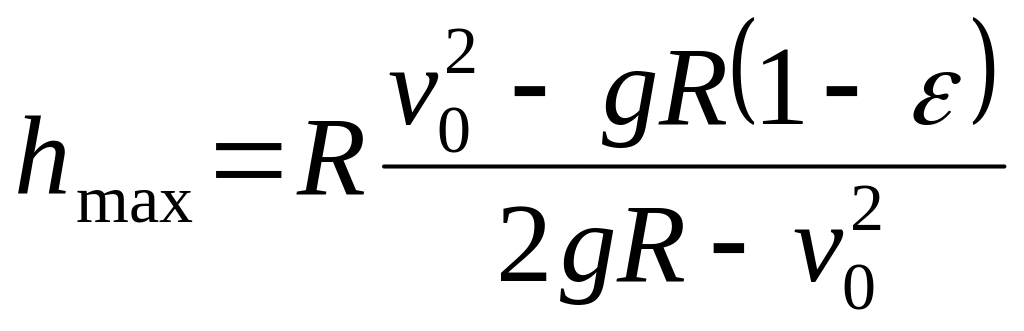
Угол между осью Оx и направлением на точку вылета

находится из уравнения орбиты (2.71), в котором r полагается

равным R:

.

Зная , получим угол между направлениями на точки выле- та и падения

,

отсюда определим дальность полета

.

Время полета получим, исполь-. зуя решение (2.78). Учитывая, что в этом решении приняты начальные условия (2.77), момент начала движения тела с поверхности Земли и соответствующее ему значение параметра определим так:

где

(см. формулу (5) примера 2.3).

2.5Движение центра масс; законы изменения и сохранения импульса системы

Как будет ясно из дальнейшего, закон изменения импульса механической системы тесно связан с понятием о центре масс. Центром масс или центром инерции механической системы называется воображаемая точка, которая как бы обладает массой, равной массе всей системы, и положение которой определяется радиусом-вектором

, (2.89)

где и — масса и радиус-вектор -той точки системы, — масса всей системы, a N— число материальных точек системы. Скорость центрамасс можно получить, продифференцировав левую и правую части (2.89) по времени:

. (2.90)

Аналогично найдем ускорение центра масс:

. (2.91)

Из определений .(2.89), (2.90) и (2.91) вытекают некоторые свойства центра масс, его скорости и ускорения. Например, скорость и ускорение, приобретаемые центром масс в результате движения i-той точки (см. рис. 2.9, на котором изображена система двух точек), будут равны и соответствен- но. Таким образом, скорость и ускорение центра масс, связанные с движением только i-той точки, параллельны соответственно скорости и ускорению - этой точки и в раз меньше их по величине. Импульсом механической системы Р называется сумма импульсов точек системы

(2.92)

где — импульс -той

точки. Согласно импульс системы равен массе всей системы, умноженной на скорость центра масс, т. е.

, (2.93)

а согласно производная импульса по времени равна массе системы, умноженной на ускорение центра масс:

. (2.94)

Заметим, что определение импульса системы в виде аналогично определению импульса одной материальной точки. Уравнение движения цент-

ра масс можно получить с помощью уравнений движения материальных точек , так как движение центра масс этой воображаемой точки обусловлено движением отдельных реальных точек механической системы. Из

следует, что

; (2.95)

однако в инерциальной системе отсчета произведение маосы какой-либо точки на ее ускорение согласно второму закону Ньютона должно быть равно , приложенной к этой точке, т. е.

. (2.96)

Следовательно, произведение массы всей системы на ускорение центра масс ввиду должно быть равно сумме всех сил, действующих на отдельные точки системы (см. рис. 2.9, в):

(2.97)

Где a — сила, действующая на -тую точку.

Среди сил, действующих на точки системы, есть как внутренние, так и внешние силы. Под внутренними силами понимают силы, действующие между точками данной механической системы, а под внешними силы, действующие на точки данной системы со стороны тел, не входящих в эту систему. Деление сил на внутренние (и внешние зависит от того, какую систему мы считаем данной, движение какой системы изучается. Если система выбрана, то силу, действующую на ее точку, всегда можно записать в виде

(2.98)

Где сумма внутренних сил, действующих на i-тую точку, сила, действующая на -тую точку со стороны -той точки системы, a - суммарная внешняя сила, действующая на -тую точку. Складывая все силы , действующие на точки системы, находим

. (2.99)

Однако сумма всех внутренних сил равна нулю, поскольку силы взаимодействия каждой пары точек равны по величине и противоположны по направлению. Действительно, представляя сумму всех внутренних сил в виде

(2.100)

и применяя третий закон Ньютона к каждой паре точек системы (см. 2.60)), найдем

(2.101)

Таким образом, из уравнения (2.97) получаем уравнение движения центр

масс относительно инерциальной системы отсчета

, (2.102)

Где -сумма всех внешних сил, действующих на точки системы. Уравнение (2.102) ввиду соотношения (2.94) приводит к закону изменения импульса

(2.103)

На основании (2.103) в полной аналогии со случаем одной материальной точки (см. 2.5)) можно утверждать, что если проекция суммы внешних сил на некоторую неподвижную ось в любой момент времени равна нулю, то проекция импульса системы или проекция, скорости центра масс системы на ту же ось сохраняется. Например, если

То

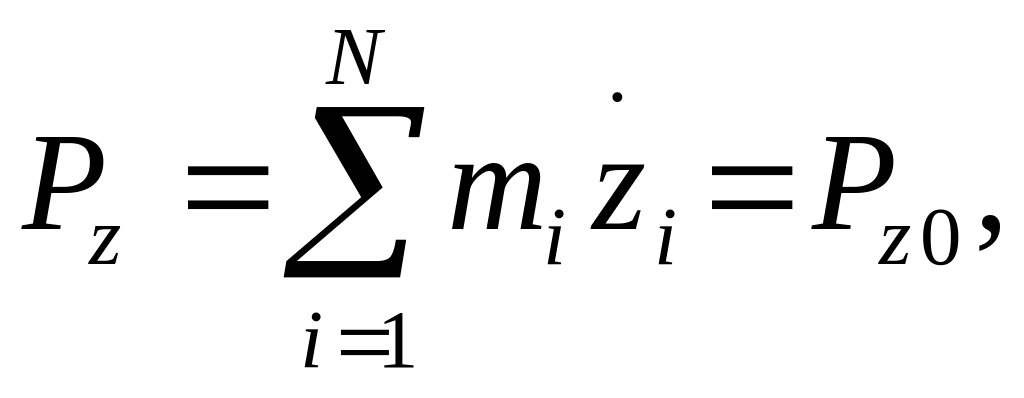(2.104)

Или

Следовательно, в направлении оси центр масс системы движется равномерно

(2.105)

Теперь рассмотрим замкнутую, или изолированную, систему, т. е. систему, взаимодействием которой с прочими не входящими в нее телами можно пренебречь *. Для такой системы все внешние силы равны нулю:

И поэтому

(2.106)

Или

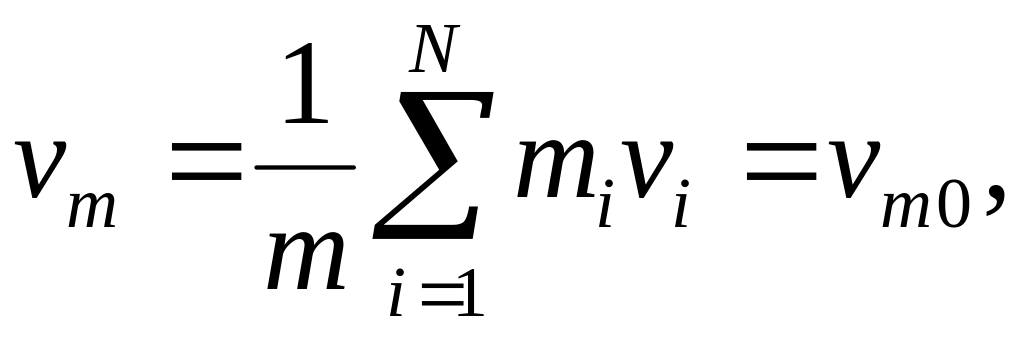
т.е имеет место закон сохранения импульса замкнутой системы.Центр масс замкнутой системы движется равномерно и прямолинейно, а ее внутренние силы не могут изменить скорости центра масс (или импульса системы). Например, солнечная система с определенной степенью точности может рассматриваться как замкнутая, и поэтому силы взаимодействия между ее телами не влияют на равномерное и прямолинейное движение центра масс системы, хотя все тела, входящие в солнечную систему, движутся ускоренно.В случае незамкнутой системы внутренние силы, вообще говоря, влияют на изменение импульса и ускорение центра масс системы, если сумма внешних сил зависит от положения или скоростей точек системы. Действительно, изменение импульса системы определяется вектором, —суммой всех внешних сил, действующих на систему (см. 2.103)), причем вектор считается

известной функцией радиусов-векторов точек и их скоростей. Однако радиусы-векторы и скорости точек изменяются под воздействием как внешних, так и внутренних сил согласно уравнениям движения

.

Вместе с тем изменяются аргументы вектора и как следствие этого изменяется сам вектор . Влияние внутренних сил на ускорение центра масс подробно проиллюстрировано на примере (2.6).Подчеркнем, что закон сохранения импульса справедлив и для таких замкнутых систем, поведение которых не подчинено уравнениям Ньютона. Например, при исследовании движения системы заряженных частиц, среди внутренних сил которой есть электромагнитные силы, было обнаружено излучение электромагнитных волн. Это излучение, как оказалось, обладает импульсом, в связи с чем импульс собственно зарядов не сохраняется. Однако суммарный импульс зарядов -и электромагнитного поля остается неизменным, т. е. имеет место закон сохранения импульса замкнутой системы, под которой в данном случае следует понимать совокупность зарядов и поля излучения.