Индивидуальное задание по летней производственной практике

1. По производственной практике

   1. Используя свойства распознавания текста программой DjVuBrowserPlugin_DL, распознанный фрагмент текста перенести в предлагаемый Вам шаблон документа Word, в котором определены стили в соответствии с правилами оформления дипломных и курсовых работ. Текстовые фрагменты в редактор MS Office 2003 переносится с использованием последовательности команд: Правка/специальная вставка/неформатированный текст.

   2. Формулы в редакторе Equation 3.0 или Math Type набираются вручную. Рекомендуется, выбрав: меню/selection/select Region, выделить формулу как рисунок, скопировать в буфер обмена, а, затем скопировать в документ Word. После чего открываете окно редактора формул Equation 3.0 или Math Type и набираете формулу. После набора формулы временный рисунок формулы удаляете.

   3. Рисунки в документе Word помещены мною уже в отдельном окне (с помощью инструмента «Добавить рисунок Word». Это растровые рисунки. Но основе этих растровых рисунков создаются векторные рисунки средствами редактора Word. После окончания векторного рисунка растровый рисунок удаляется

   4. Текст, рисунки, таблицы и подписи к ним осуществляются в соответствии с правилами оформления дипломных работ.

Структура заголовков

Стили заголовков установлены в соответствии со стандартом оформления дипломной работы. Чтобы создать оглавление, установите курсор в той части документа, где должно быть оглавление (в дипломной работе это сразу после страницы с рефератом – 3-я страница) и выберите в меню: вставка/ссылка/оглавления и указатели/оглавление.

Содержание

1 Основные понятия и законы механики 8

1.1 Понятия о материальной точке, о пространстве и времени 8

1.1.1 Закон движения материальной точки. Понятие траектории (начало задания 2, стр. 14) 10

1.1.2 Пример 1.1. Траектория, скорость и ускорение материальной точки в декартовых координатах (начало задания 3 Левковский, стр. 20) 13

1.1.3 Пример 1.2. Траектория, скорость и ускорение материальной точки в цилиндрических координатах 14

1.1.4 Пример 1.3. Ускорение точки, движущейся по эллипсу с постоянной относительно фокуса эллипса секторной скоростью 15

1.1.5 Пример 1.4. Ускорение точки, движущейся по эллипсу с постоянной относительно центра эллипса секторной скоростью 16

1.1.6 Пример 1.5. Определение положения точки по ее скорости 16

1.2 Понятия о силе и массе (начало задания 4 Сергеев, стр. 26) 16

1.2.1 Начальные условия 16

1.2.2 Упругая сила (стр. 29) 17

1.2.3 Сила Лоренца (стр. 30) 17

1.2.4 Сила сопротивления среды, зависящая от скорости 17

1.2.5 Закон всемирного тяготения (начало задания 5 Элькарамов, стр. 33) 18

1.3 Понятие об инерциальной системе отсчета и законы Ньютона. Принцип относительности Галилея 18

1.4 Решение уравнений движения и начальные условия (начало задания 6 Солнышкин, стр. 41) 20

1.4.1 Пример 1.6. Заряженная частица в переменном электрическом поле 20

1.4.2 Пример 1.7. Задача о пространственном осцилляторе 21

1.4.3 Пример 1.8. Движение в однородном поле тяжести при наличии силы сопротивления 21

1.4.4 Пример 1.9. Движение заряженной частицы в постоянных однородных электрическом и магнитном полях (начало задания 7 Денисов, стр. 51) 23

2 Законы изменения и сохранения импульса, кинетического момента и энергии (начало задания 8 Леошко, стр. 60) 26

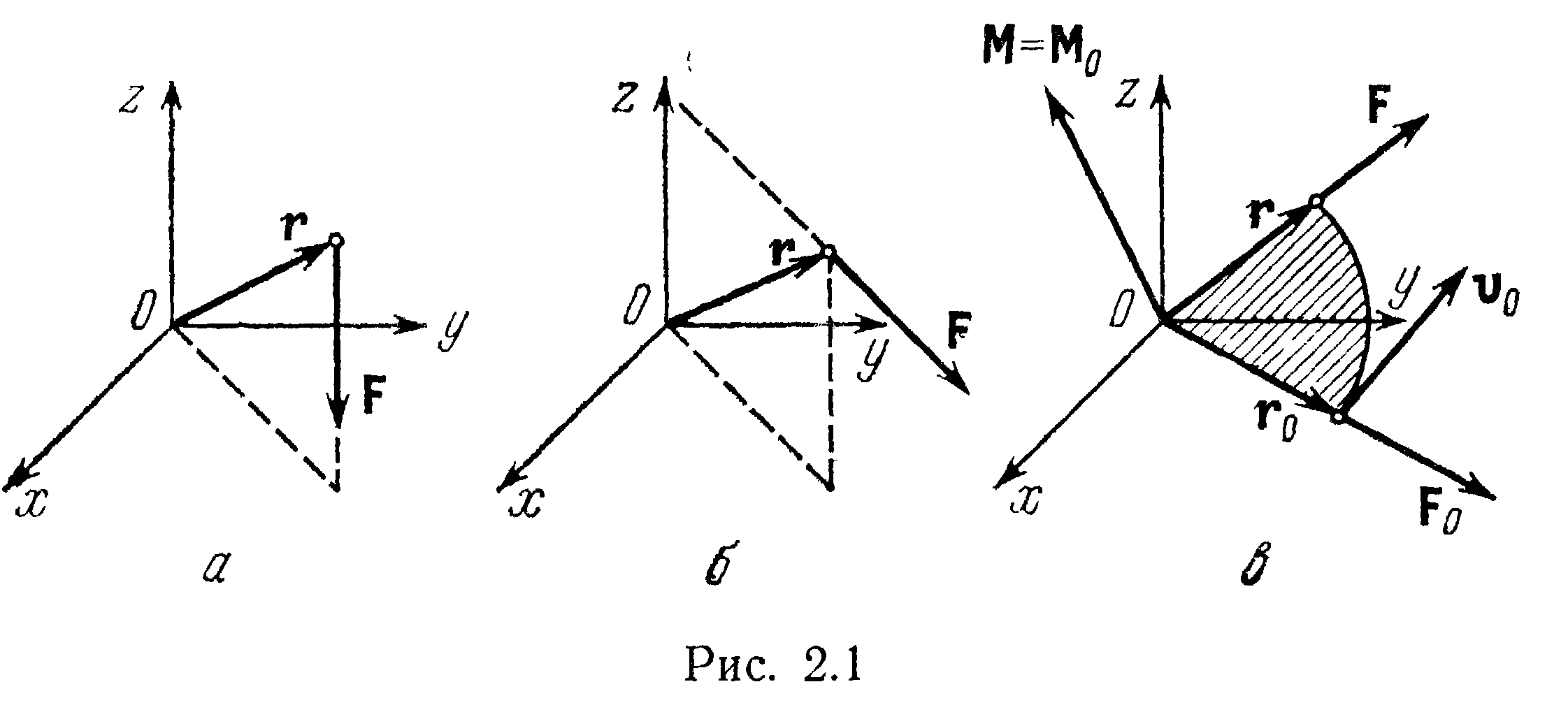
2.1 Законы изменения и сохранения импульса и момента импульса материальной точки 26

2.1.1 Интегралы движения 26

2.1.2 Закон изменения импульса материальной точки 26

2.1.3 Закон изменения момента импульса точки 26

2.2 Законы изменения и сохранения энергии материальной точки 27

2.2.1 Потенциальные силы 27

2.2.2 Гироскопические силы (начало задания 9 Тимошенко, стр. 70) 28

2.2.3 Диссипативные силы 28

2.2.4 Теорема Клаузиуса о вириале сил 28

2.2.5 Пример 2.1 Движение через потенциальный барьер 28

2.2.6 Пример 2.2. Заряд в неоднородном магнитном поле 28

2.3 Движение в центрально-симметричном поле 28

2.4 Движение под действием силы, обратно пропорциональной квадрату расстояния до центра силы. Законы Кеплера (начало задания 10 Плотников, стр. 82) 31

2.4.1 Пример 2.3. Изменение орбиты космического корабля (начало задания 11 Кондратенко, стр. 89) 33

2.4.2 Пример 2.4. Движение по баллистической траектории 33

2.5 Движение центра масс; законы изменения и сохранения импульса системы 34

2.5.1 Понятие центра масс (центра инерции) системы материальных точек 34

2.5.2 Импульс системы материальных точек 34

2.5.3 Пример 2.5. Движение центра масс в однородном поле 36

2.5.4 Пример 2.6. Движение центра масс в неоднородном поле (начало задания 12 Голубь, стр. 99) 36

2.5.5 Пример 2.7. Движение тела переменной массы; задача Циолковского 36

2.6 Законы изменения и сохранения кинетического момента системы 36

2.6.1 Пример 2.8, Изменение моментов импульсов точек замкнутых систем 37

2.7 Законы изменения и сохранения энергии системы 37

3 Задача двух тел и теория рассеяния частиц (начало задания 13 Хилько, стр. 113) 38

3.1 Задача двух тел 38

3.2 Упругое рассеяние частиц (начало задания 14 Коробейников, стр. 121) 39

3.2.1 Диаграмма скоростей относительно лабораторной системы отсчета (начало задания 15 Балабас, стр. 127) 40

3.2.2 Пример 3.1. Рассеяние двух частиц, одна из которых до рассеяния покоится 41

3.2.3 Пример 3.2. Рассеяние двух частиц, скорости которых до рассеяния равны по величине и противоположны по направлению 42

3.2.4 Пример 3.3. Рассеяние двух частиц с электростатическим взаимодействием (начало задания 16 Тимеркеев, стр. 135) 43

3.2.5 Пример 3.4. Рассеяние двух однородных абсолютно упругих шариков 43

3.3 Поперечные сечения рассеяния (начало задания 16 Гарибян, стр. 143) 45

3.3.1 Рассеяние одного пучка частиц на другом пучке 45

3.3.2 Дифференциальное эффективное поперечное сечение рассеяния 45

3.3.3 Полное эффективное сечение рассеяния 45

3.3.4 Пример 3.5. Дифференциальные сечения рассеяния частиц с электростатическим взаимодействием; формула Резерфорда (начало задания 17 Горвиц, стр. 143) 46

3.3.5 Пример 3.6. Дифференциальное сечение рассеяния однородных абсолютно упругих шариков 46

4 Движение относительно неинерциальных систем отсчета 47

4.1 Положение системы отсчета 47

4.1.1 Углы Эйлера 47

4.1.2 Простейший случай, когда ориентация системы определяется одним углом (начало задания 18 Савин, стр. 152) 48

4.2 Поступательное движение и изменение ориентации системы отсчета 49

4.2.1 Поступательное движение системы отсчета 49

4.2.2 Изменение ориентации при неизменном положении начала системы S' 50

4.2.3 Повороты твердой квадратной пластинки 51

4.2.4 Угловая скорость 53

4.2.5 Пример 4.1. Регулярная прецессия твердого тела (начало задания 19, стр. 161) 53

4.3 Общий случай движения системы отсчета 54

4.4 Положение, скорость и ускорение материальной точки относительно разных систем отсчета 55

4.5 Уравнение движения материальной точки относительно неинерциальной системы отсчета; силы инерции (начало задания 20, стр. 171) 56

4.5.1 Пример 4.3. Уравнение движения точки относительно Земли 56

4.5.2 Пример 4.4. Отклонение падающего (или взлетающего) тела от вертикали 57

4.5.3 Пример 4.5. Состояние невесомости 57

4.6 Законы изменения кинетического момента и кинетической энергии относительно поступательно движущейся системы центра масс 57

1Основные понятия и законы механики

1.1Понятия о материальной точке, о пространстве и времени

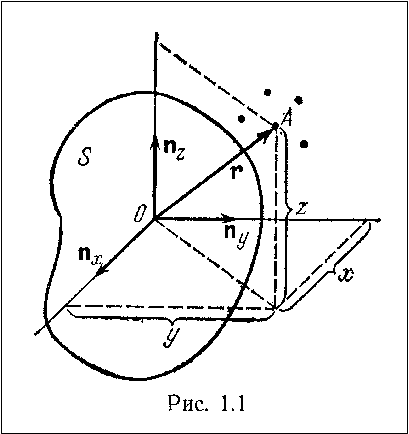
1. Определение базиса

2. Перемещение базиса

по сравнению со скоростью света¹. (конец задания 1)

1.1.1Закон движения материальной точки. Понятие траектории (начало задания 2, стр. 14)

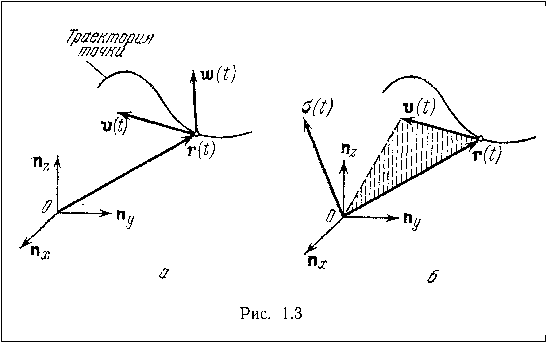
3. К определению скорости точки

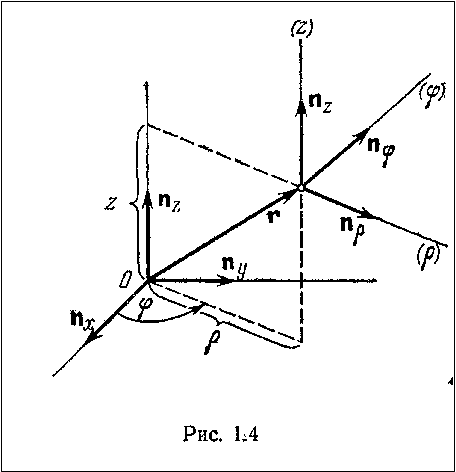
4. Цилиндрические координаты

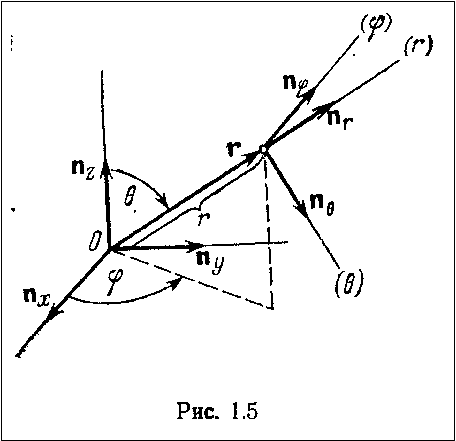
5. Сферические координаты

6. Естественный трехгранник

возможность решать кинематические задачи, т. е. задачи, в которых движение описывается вне связи с причинами, вызывающими это движение. (конец задания 2)

1.1.2Пример 1.1. Траектория, скорость и ускорение материальной точки в декартовых координатах (начало задания 3 Левковский, стр. 20)

Закон движения точки относительно системы отсчета S

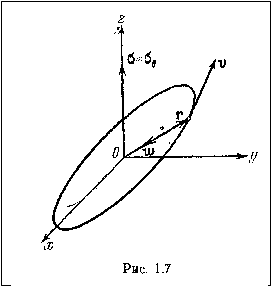
7. Траектория, скорость и ускорение материальной точки в декартовых координатах

1.1.3Пример 1.2. Траектория, скорость и ускорение материальной точки в цилиндрических координатах

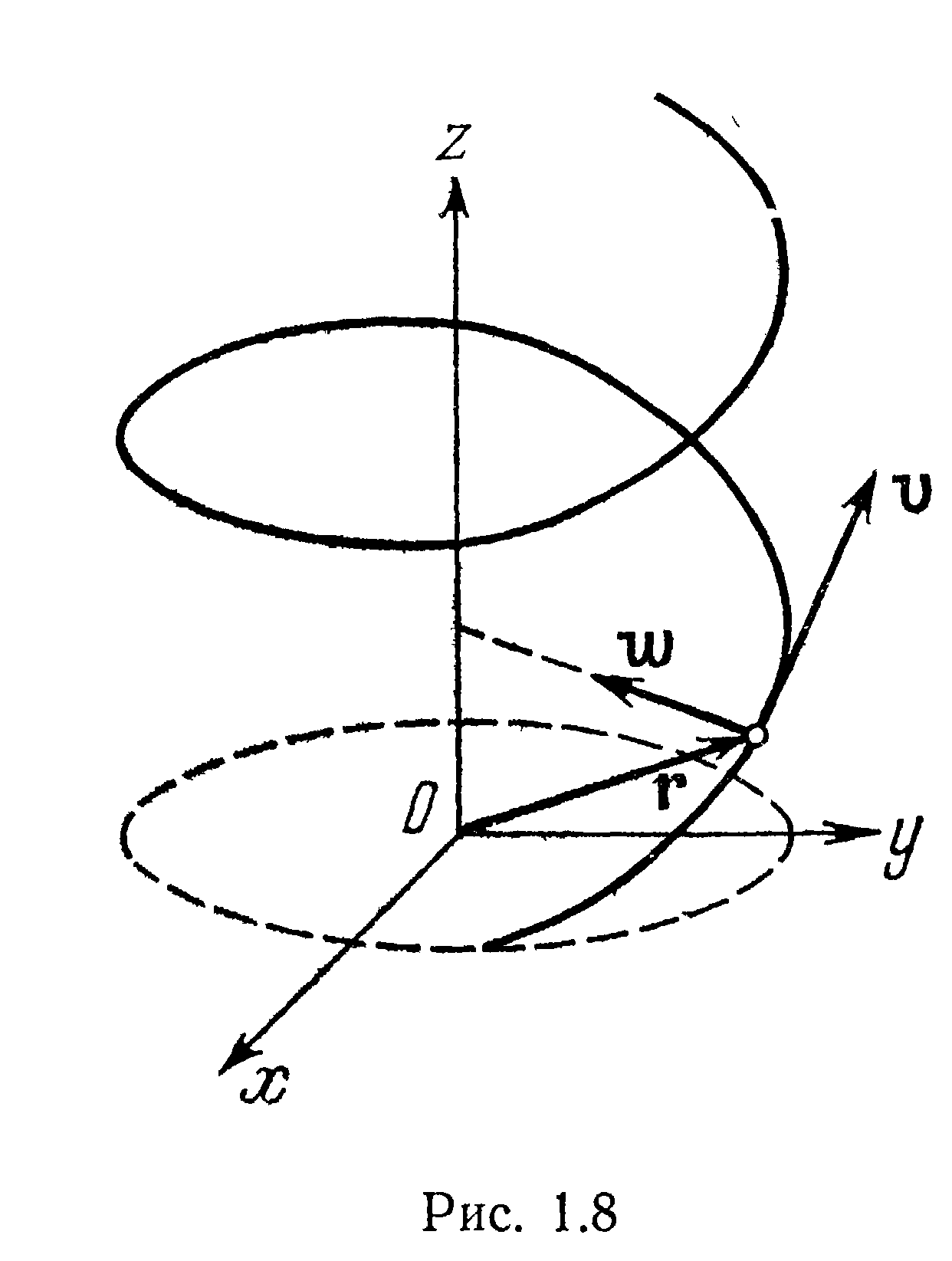
8. Движение по винтовой линии

Таким образом, точка движется по прямой с постоянной линейной и секторной скоростями (рисунок 9).

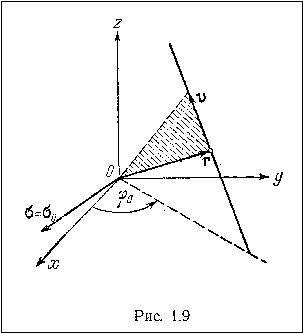
9. Движение по прямой с постоянной линейной и секторной скоростями

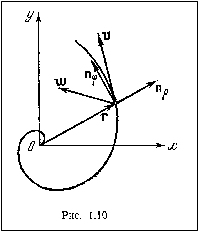
10. Архимедова спираль

1.1.4Пример 1.3. Ускорение точки, движущейся по эллипсу с постоянной относительно фокуса эллипса секторной скоростью

11. Движение по эллиптической траектории

1.1.5Пример 1.4. Ускорение точки, движущейся по эллипсу с постоянной относительно центра эллипса секторной скоростью

Точка движется по эллипсу с полуосями a и b. Ее

1.1.6Пример 1.5. Определение положения точки по ее скорости

(конец задания 3 Левковский, стр. 26)

1.2Понятия о силе и массе (начало задания 4 Сергеев, стр. 26)

1.2.1Начальные условия

12. Движение материальной точки вблизи поверхности Земли

13. Влияние заряженных тел

1.2.2Упругая сила (стр. 29)

1.2.3Сила Лоренца (стр. 30)

1.2.4Сила сопротивления среды, зависящая от скорости

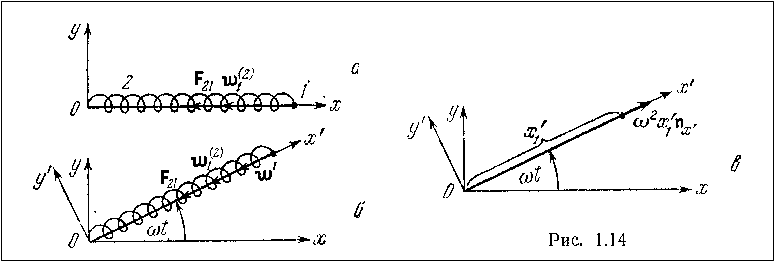
14. Движение материальной точки по горизонтальному идеально гладкому стержню

. (1.48)

(конец задания 4 Сергеев, стр. 33)

1.2.5Закон всемирного тяготения (начало задания 5 Элькарамов, стр. 33)

1.3Понятие об инерциальной системе отсчета и законы Ньютона. Принцип относительности Галилея

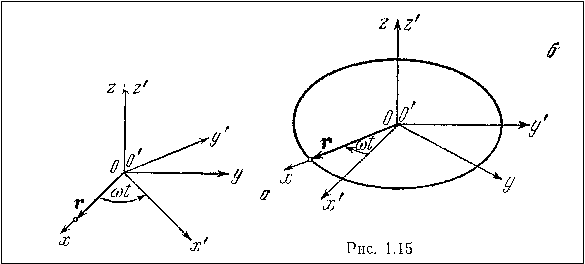
15. Вращение системы отсчета

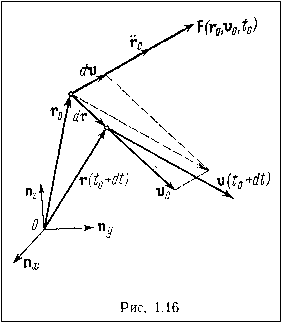
16. Определение скорости и ускорения по заданной силе

17. Третий закон Ньютона

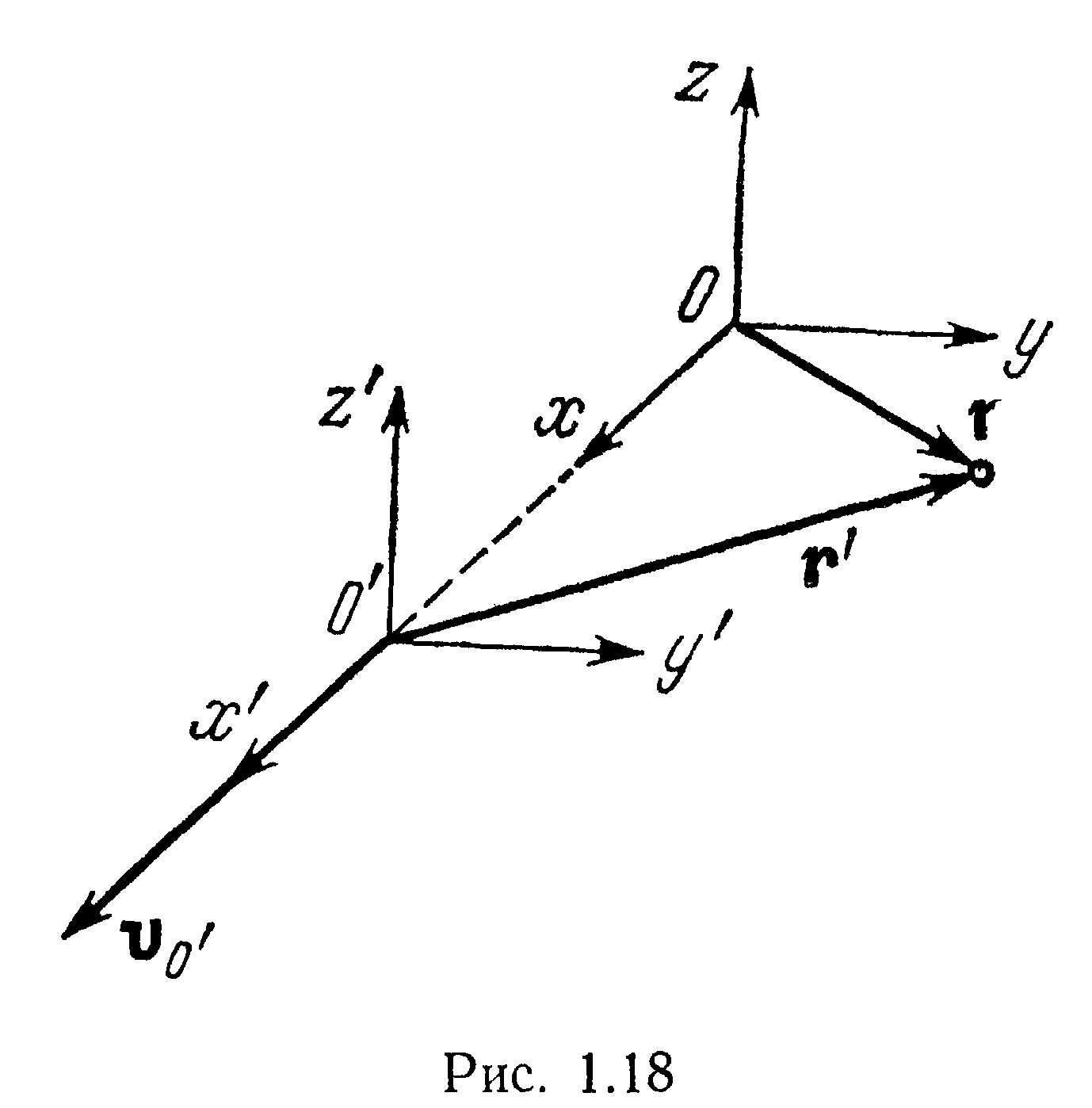
18. К выводу преобразований Галилея

(конец задания 5 Элькармов, стр. 41)

1.4Решение уравнений движения и начальные условия (начало задания 6 Солнышкин, стр. 41)

1.4.1Пример 1.6. Заряженная частица в переменном электрическом поле

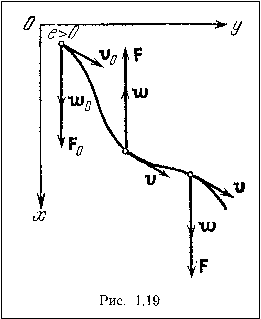
19. Плоское движение точки

1.4.2Пример 1.7. Задача о пространственном осцилляторе

1.4.3Пример 1.8. Движение в однородном поле тяжести при наличии силы сопротивления

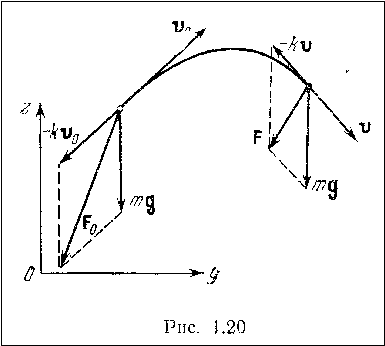
20. Скорость и ускорение при плоском движении

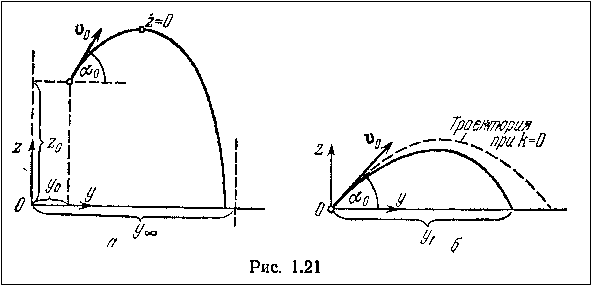
21. Движение тела, брошенного под углом к горизонту

(конец задания 6 Солнышкин, стр. 51)

1.4.4Пример 1.9. Движение заряженной частицы в постоянных однородных электрическом и магнитном полях (начало задания 7 Денисов, стр. 51)

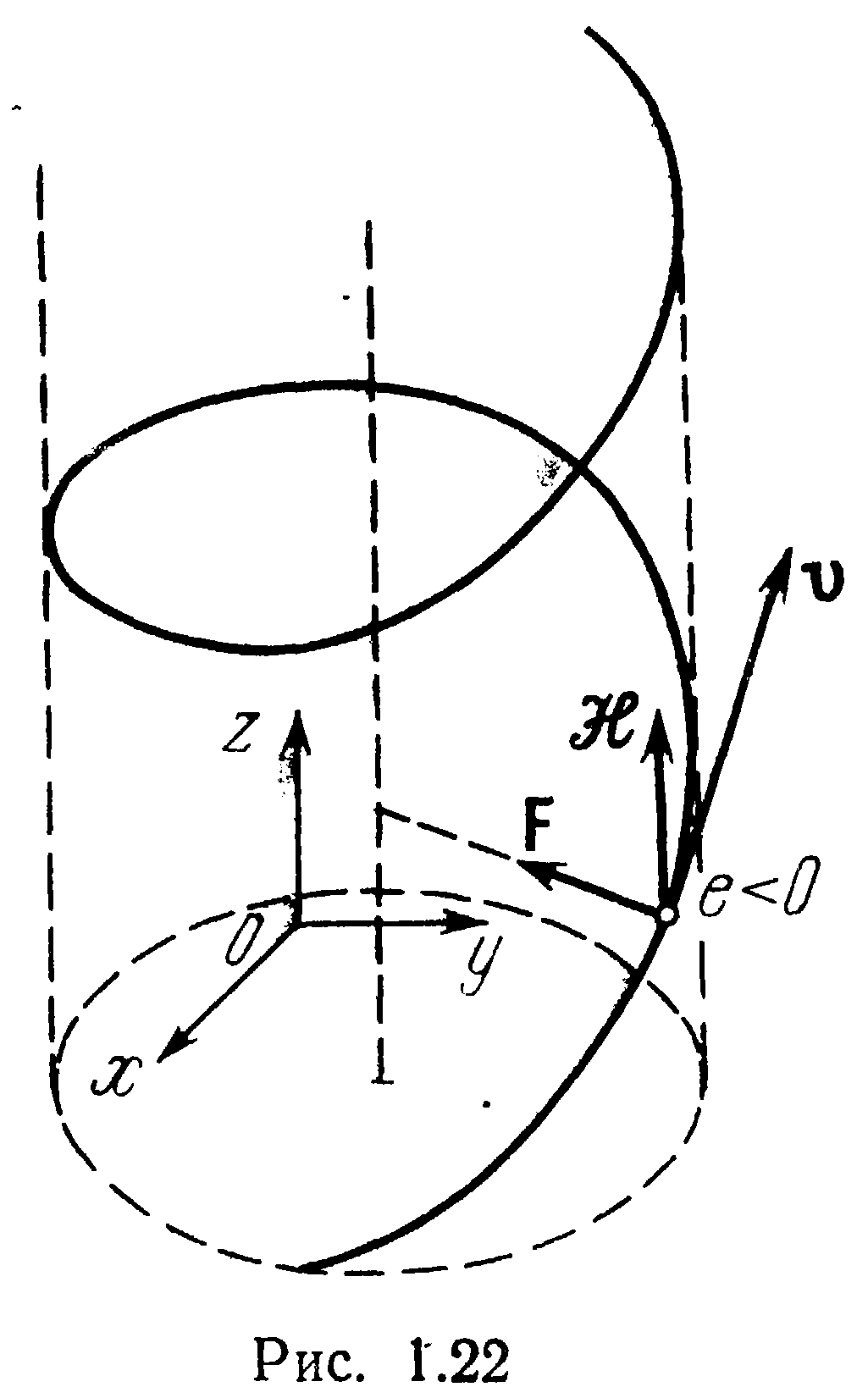
22. Движение заряженной частицы в электрическом и магнитном полях

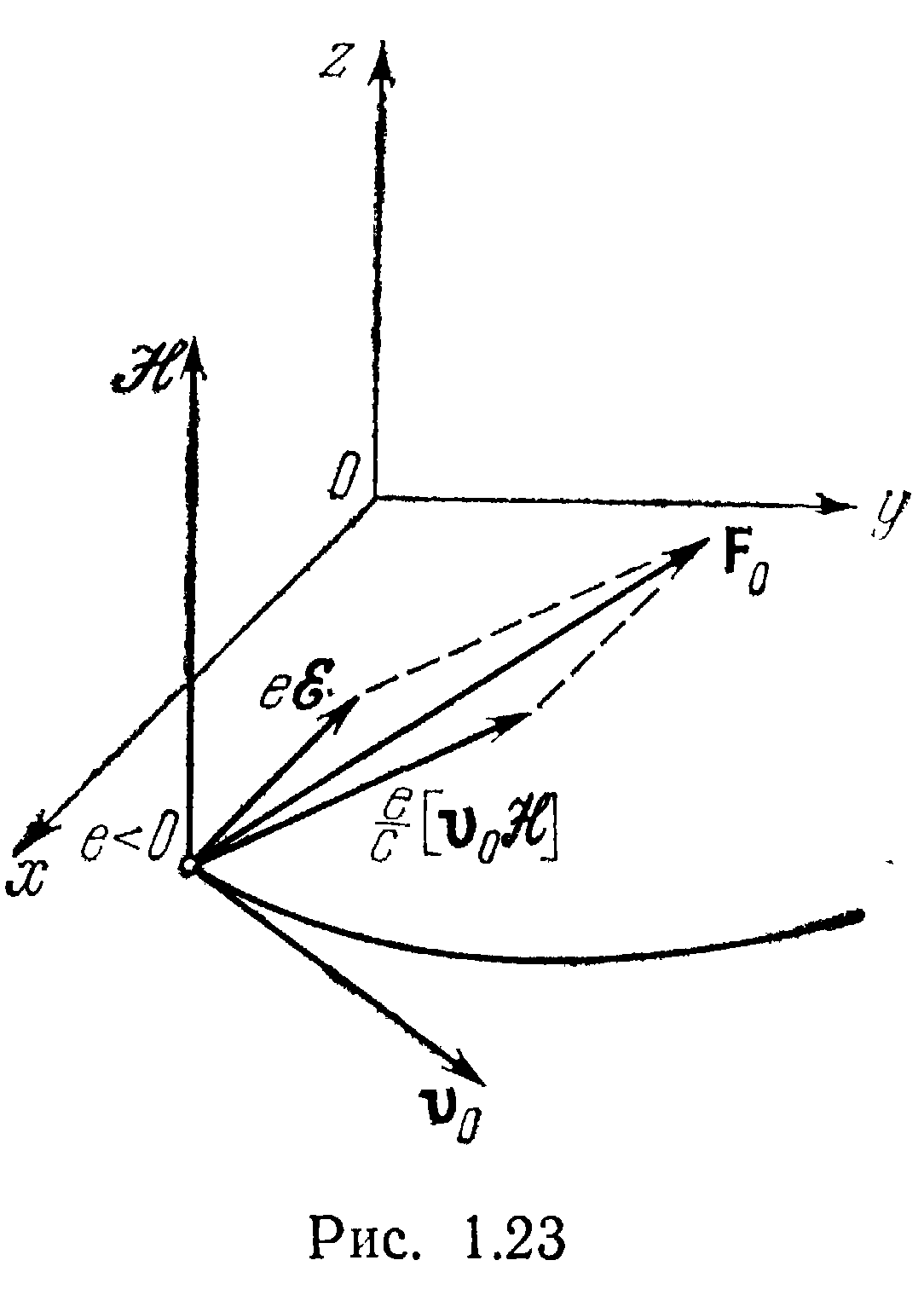
23. Выбор координатных осей

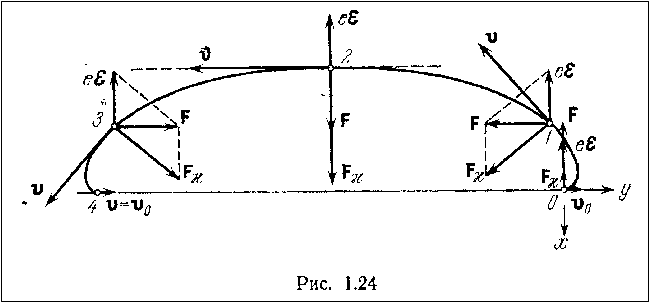
24. Вращение вокруг движущегося центра

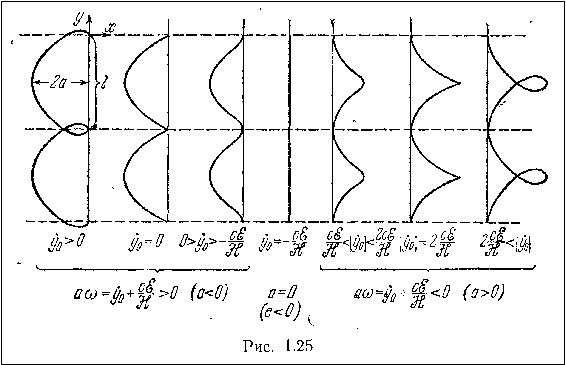
25. Дрейф частиц

(конец задания 7 Денисов, стр. 59)

2Законы изменения и сохранения импульса, кинетического момента и энергии (начало задания 8 Леошко, стр. 60)

2.1Законы изменения и сохранения импульса и момента импульса материальной точки

2.1.1Интегралы движения

Из дальнейшего будет ясно, что законы сохранения импульса, кинетического момента и энергии приводят к так называемым интегралам движения.

2.1.2Закон изменения импульса материальной точки

2.1.3Закон изменения момента импульса точки