Тема 4. Электронные оболочки атомов и периодическая система элементов.

4.1. Квантовые числа электронов в сложном атоме и принцип Паули.

В сложном атоме, содержащем 2 и более электронов, эти электроны взаимодействуют между собой, и поэтому, нельзя считать, что каждый электрон двигается в поле ядра независимо от всех остальных. Однако приближенно действие всех остальных электронов на данный электрон можно заменить некоторым усредненным, эффективным полем, обладающем сферической симметрией и убывающем с увеличением расстояния r рассматриваемого электрона от ядра. Дополнительная потенциальная энергия электрона U_доп в этом поле будет функцией от r, и полная потенциальная энергия электрона в поле ядра и остальных электронов запишется в виде:

(4.1)

С точки зрения наглядных представлений все остальные электроны образуют сферически симметричное электронное облако, и на электрон, находящийся на расстоянии r от ядра, действует, наряду с зарядом ядра z, заряд всех электронов, расположенных внутри сферы радиуса r, что приводит к экранированию ядра электронами.

Потенциал можно представить:

, (4.2)

где - функция расстояния, характеризующая экранирование ядра электронами. С помощью (6.2) формула (6.1) запишется в виде:

(4.3)

где - эффективный заряд ядра, действующий на электрон на расстоянии r. Это такой заряд ядра, при котором для силы, обратно пропорциональной квадрату расстояния (кулоновской силы), потенциал на данном расстоянии r равен U(r).

Функция экранирования с расстоянием возрастает от при r =0 до постоянного значения на - ти. При r на электрон будет действовать поле ядра за вычетом поля всех электронов, кроме одного, и для нейтрального атома .

Электрон в сферически симметричном поле можно характеризовать набором квантовых чисел:

Рассмотренное приближение (внешний электрон + атомный остаток) называют одноэлектронным приближением.

Очень важен вопрос о зависимости энергии электрона от квантовых чисел. Энергия будет теперь зависеть не только от n, но и от . Для поля типа (6.3), убывающего с расстоянием более быстро, чем кулоновское (с увеличением r одновременно уменьшается Z(r), стоящее в числителе), энергия электрона тем меньше при заданном n, чем меньше .

Физическая причина подобной зависимости состоит в том, что электоны с меньшим подходят ближе к ядру, где Z(r) больше, что увеличивает их энергию связи. Подробно мы рассмотрим этот вопрос дальше.

Энергию электрона как функцию n и можно представить в виде, аналогичном формуле (5.3):

(4.4)

где введён -эффективный з-д. Как правило, < Z и его записывают в виде:

(4.5)

где – постоянная экранирования, являющаяся функцией от n и от .

Рассмотрим теперь сложный атом с числом электронов N. Его состояние в одноэлектронном приближении будет характеризоваться совокупностью квантовых чисел:

; ; … ; .

Если атом содержит 1 электрон, этот электрон может находиться в любом состоянии, для которого:

n=1,2,3…; =0,1,2…n-1; = , -1,…,- ; .

Для атома содержащего два и более электронов, возможные состояния отдельных электронов определяются принципом Паули:

в атоме не может быть двух электронов в одинаковых состояниях, т.е. не может быть двух электронов, характеризуемых одинаковыми наборами квантовых чисел , , , .

Любые два электрона должны отличаться значением хотя бы одного из 4-х квантовых чисел.

Принцип Паули позволяет определить возможное число электронов в атоме, обладающих заданными значениями определённых квантовых чисел.

1. Если задано значение n и , то, согласно формуле g_l = 2(2•l+1), возможны 2(2 +1) состояний, отличающихся значениями и . Следовательно, в атоме может быть не более электронов с заданными и .

Т.О., при заданном в атоме может иметься:

2(2•0+1)=2 S-электрона ( =0),

2(2•1+1)=6 P-электронов ( =1) и т.д.

2. Если задано значение , то возможны 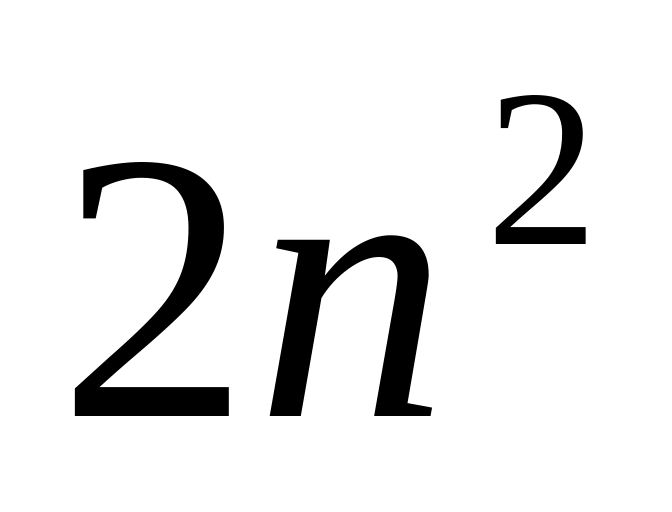состояний, отличающихся значениями , и (см. (5.2)) следовательно, в атоме может быть не более электронов с заданным n, т.е. может иметься 2, 8, 18, 32… электронов с n=1, 2, 3, 4…

n=1
n=2
n=3
n=4
n=5
…	…	…

Электроны с одинаковыми n и называются эквивалентными электронами. Их обозначают символами ns, np, nd, nf…для =0, 1, 2, 3…и указывают число таких электронов в виде показателя у символа, например, …

Возможные числа эквивалентных электронов в таблице 1

Сумма показателей в горизонтальном ряду даёт полное число электронов 2n², т.е. 2, 8, 18…

Совокупность значений n и для всех N электронов в атоме , , …, характеризует электронную конфигурацию.