3.5. Зависимость спектров одноэлектронных атомов от заряда и массы ядра.

Формула Бора для атома водорода является частным случаем общих формул для уровней энергии одноэлектронных атомов. Эти формулы были впервые получены Бором в 1913 году на основе модельных представлений его теории, а затем выведена последовательным квантово-механическим методом Шредингером в 1926 году. Они имеют вид:

(n=1.2.3…) (3.5.1)

, (3.5.2)

где постоянная Ридберга:

,

(3.5.3 ) - приведенная масса электрона и ядра.

Введением приведенной массы учитывается тот факт, что в атоме движется не только электрон, но и ядро, и движение происходит вокруг общего центра масс.

Уровни энергии и частоты переходов для членов изоэлектронного ряда отличаются масштабом, который увеличивается пропорционально . R согласно (5.5.3) мало меняется с массой ядра , то есть этот масштаб определяется множителем , т.е. возрастает пропорционально . Спектральные серии для водородоподобных ионов аналогичны спектральным сериям атома H, только смещены в коротковолновую область.

Несмотря на малость отличия приведенной массы m от массы электрона , все же необходимо учитывать зависимость m от массы ядра M. Значения R несколько отличаются как для разных элементов, так и для изотопов одного элемента. Отличия составляют сотые доли процента. Однако этого достаточно для того, чтобы их измерить. Дважды в истории развития физики они сыграли существенную роль: первый раз, когда Бору в 1913 году удалось истолковать некоторые спектральные серии, приписываемые водороду, как серии ионизированного ; и второй раз в 1932 году, когда по наличию слабых спутников линий серии Бальмера был открыт тяжелый водород - дейтерий.

3.6. Характеристика стационарных состояний одноэлектронного атома.

С точки зрения модельных представлений Бора, стационарного состояния соответствуют движению электрона по определенным орбитам.

Бор получил радиус круговой орбиты

(формула Бора для радиуса круговой орбиты)

Т.е. любому уровню энергии соответствует своя орбита.

При более общем решении задачи об одноэлектронном атоме, на основе модельных представлений Бора, получается движение по эллиптическим орбитам.

Эллиптические орбиты, соответствующие n = 1, 2, 3 показаны на рис.1.

При n=1 возможна лишь круговая орбита, а при n=2, 3 - круговая и эллиптические. Причем, чем меньше орбитальный момент, тем эллипс более вытянут и тем меньше минимальное расстояние, на которое электрон подходит к ядру.

П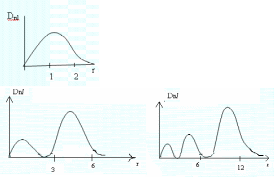 ерейдем теперь к квантовомеханической характеристике стационарных состояний одноэлектронного атома.

Решение квантово механической задачи приводит к формуле (3.5.1) для уровней энергии и позволяет характеризовать вырожденные состояния с различными и (при заданном n) наглядным образом при помощи распределения электронной плотности. Заряд электрона при этом рассматривается как непрерывно распределенный по объёму атома с некоторой плотностью т.о., что полный заряд равен e, т.е.

.

Т.е. электрон нельзя локализовать, и любому состоянию сопоставляется пространственное распределение электронной плотности - некое электронное облако.

П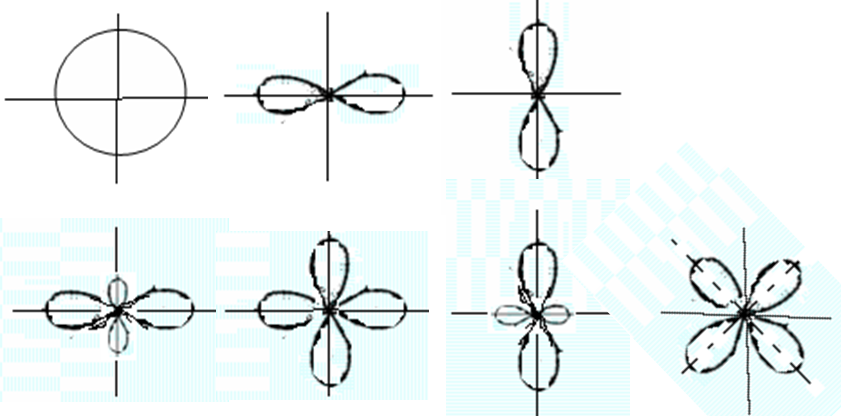 редставление об электронном облаке правильнее отражают свойства электрона в атоме, чем модельные представления теории Бора.

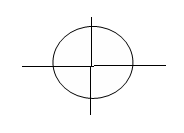
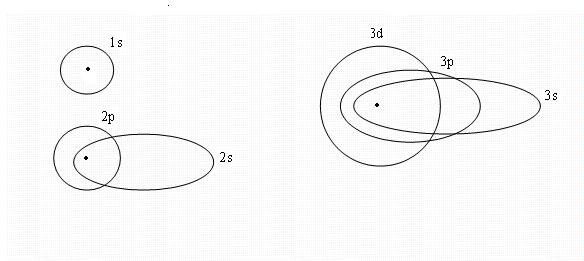
Для состояний одноименного атома распределение в первую очередь зависит от , при =0 оно является сферически симметричным и имеет максимум в начале координат (где находится ядро); для >0 электронная плотность в начале координат равна нулю. С увеличением n плотность облака уменьшается, и оно занимает всё большую область. Можно задать так называемое радиальное распределение электронной плотности-рис.2.

При = n-1, т.е. для состояний 1s, 2p, 3d получается только один максимум. С уменьшением число максимумов при заданном n увеличивается, причем первый максимум приближается к ядру, а последний удаляется от него, т.е. распределение электронной плотности растягивается вдоль радиуса. Это соответствует переходу от круговых орбит к эллиптическим (рис.2).

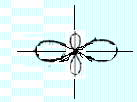
Угловое распределение электронной плотности характеризуется функцией , оно показано на рисунках ниже.

Распределение электронной плотности играет важную роль при рассмотрении вопросов взаимодействия атомов, в особенности вопросов образования химической связи между атомами в молекуле.