3.3. Правила отбора для одноэлектронных атомов.

Спектральные переходы могут происходить не между всеми парами уровней энергии. Переходы имеют место лишь при выполнении определенных условий – правил отбора.

Переходы, которые удовлетворяют правилам отбора, называют разрешенными, вероятность остальных очень низкая и они называются запрещенными.

Для главного квантового числа n возможны любые его изменения, что приводит к появлению серий, высокие члены которых могут соответствовать очень большим изменениям

Правил отбора по n не уществует.

Для орбитального квантового числа имеет место правило отбора:

С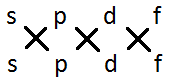 огласно правилу отбора (3.3.1) s-состояния комбинируют только с p-состояниями, p-состояния комбинируют как s-, так и с d-состояниями, d-состояния комбинируют как с p, так и с f-состояниями и т.д. Это можно представить в виде схемы:

Для орбитального магнитного квантового числа правило отбора имеет вид:

т.е. может либо сохранять своё значение, либо менять его на 1.

3.4. Тонкая структура уровней энергии и спектральных линий.

Наличие спина электрона обуславливает для одноэлектронных атомов тонкую структуру уровней энергии и тонкую структуру спектра линий, получающихся при переходах между этими уровнями.

Рассмотрим характер уровней энергии при учёте спин-орбитального взаимодействия. Благодаря спин-орбитальному взаимодействию орбитальный момент складывается со спиновым моментом в полный момент:

Его величина определяется внутренним квантовым числом j, принимающим полу целые значения

Значение проекции вектора определяется полным магнитным квантовым числом , принимающим значение от -j до j.

Т.е. получим набор еще один набор квантовых чисел:

Для уровня с заданными n, и j степень вырождения равна:

Число независимых состояний при заданных n и равно .

Док-во: Действительно, при получается состояний, а при получается состояний, т.е. всего состояний.

Рассмотрим подробнее возможные уровни энергии атома водорода при заданном n, различающиеся значениями и j.

Согласно (3.4.1), при , и получается одно значение j, а при всех других получается по два значения j:

(при и j=3 / 2, при = 2 j = 3/2 и j = 5/2 и т.д.)

Общее число уровней с различными парами и j равно . При этом j принимает n значений, меняясь от 1/2 до n-1/2, причем любое значение j встречается по два раза, кроме максимального значения, равного j= n-1/2, которое получается один раз (Док-во: .

Каждое значение также встречается по 2 раза, кроме минимального значения, равного нулю, которое получается один раз .

Итак, можем схематически изобразить уровни энергии атома водорода с различными значениями n, , j (смотри таблицу).

n		j	Обозн.
4	3	7/2	42F7/2
		5/2	42F5/2
	2	5/2	42D5/2
		3/2	42D3/2
	1	3/2	42P3/2
		1/2	42P1/2
	0	1/2	42S1/2
3	2	5/2	32D5/2
		3/2	32D3/2
	1	3/2	32P3/2
		1/2	32P1/2
	0	1/2	32S1/2
2	1	3/2	22P3/2
		1/2	22P1/2
	0	1/2	22S1/2
1	0	1/2	12S1/2

На схеме (в таблице) приведены общепринятые обозначения уровней энергии одноэлектронного атома.

Цифра впереди указывает значение n.

Буквами S, P, D, F обозначены значения = 0, 1, 2, 3 для атома в целом, а не для одного электрона для которого было s, p, d, f.

Для атома, имеющего лишь один электрон, орбитальный момент атома в целом и есть орбитальный момент электрона. В общем же случае атома со многими электронами орбитальный момент атома в целом является суммой орбитальных моментов отдельных электронов.

При учете спина полный момент принимает два значения: . Поэтому вместо любого уровня имеем два уровня - дублет. Это обозначается индексом 2, стоящим слева вверху. Этот индекс дает число возможных ориентаций спина (мультиплетность), равное в общем случае:

где S - значение спина для атома в целом.

В данном случае:

Индекс справа снизу указывает значение числа j. Этим индексом принято обозначать значение полного момента атома; в данном случае полный момент атома совпадает с полным моментом электрона.

Например: