Часть 2: Атомная спектроскопия. Тема 3. Уровни энергии и спектры атома водорода и водородоподобных ионов.

3.1. Квантовые числа одноэлектронного атома и степень вырождения его уровней.

Спектр атома водорода является простейшим атомным спектром. Это обусловлено тем, что атом H имеет простое строение и состоит из протона с зарядом +e и электрона с зарядом -e . Т.е. атом H - это одноэлектронная система.

Аналогичными спектрами будут обладать все ионы - и т.д., состоящие из ядра и также из одного электрона. Соответственно, мы будем считать заряд ядра равным +Ze, где Z = 1 для H, Z = 2 для , Z = 3 для и т.д.

Итак, мы будем говорить об одноэлектронном атоме, подразумевая нейтральный атом водорода и ионизированные атомы с одним электроном – водородоподобные ионы. Они вместе с атомом водорода образуют изоэлектронный ряд - т.е. ряд атомов с одинаковым числом электронов.

Состояние одноэлектронного атома характеризуется четырьмя квантовыми числами:

1. Главное квантовое число n принимает целые значения n = 1, 2, 3, ..., и определяет энергию стационарного состояния по формуле Бора: Е_n = -R/n².

2. Орбитальное квантовое число l определяет величину момента количества движения электрона относительно ядра (орбитальный момент). При заданном n оно принимает целые значения:

= 0, 1, 2, 3, …, n-1, т.е. n значений.

Квадрат орбитального момента равен

Состояния с различными l принято обозначать буквами:

= 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14

s p d f g h i k l m n o q r t

3. Орбитальное магнитное квантовое число 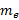определяет величину проекции орбитального момента на заданное направление. При заданном принимает целые значения:

т.е. значений (*), или

Сама проекция орбитального момента равна ħm_e .

4. Спиновое магнитное квантовое число определяет проекцию спина на фиксированную ось. Принимает два полуцелых значения:

Таким образом, характеристика стационарного электронного состояния атома водорода или водородоподобного иона дается набором четырех квантовых чисел:

3.2. Невырожденные и вырожденные уровни энергии. Вырождение уровней одноэлектронного атома.

Заданному значению энергии может соответствовать одно определенное стационарное состояние или ряд (2 и более) стационарных состояний, отличающихся друг от друга какими-либо свойствами.

ОПР. Если имеется одно стационарное состояние с заданным значением энергии, то уровень энергии называется невырожденным. Если же имеется ряд таких состояний, которым соответствует одно значение энергии, то уровень энергии называют вырожденным и говорят, что эти состояния вырождены.

ОПР. Число различных независимых состояний атомной системы с одним и тем же значением энергии Е_i называют степенью или кратностью вырождения.

Степень вырождения = 1 для невырожденных уровней и > 1 для вырожденных уровней.

Примером системы с невырожденными уровнями энергии является система с одной степенью свободы, совершающая гармонические колебания около положения равновесия - линейный гармонический осциллятор. Таким осциллятором можно считать 2-х атомную молекулу, в которой ядра колеблются друг относительно друга по оси молекулы вокруг некоторого равновесного положения. Согласно квантовой механике для линейного гармонического осциллятора получаются равноотстоящие невырожденные уровни энергии.

Примером системы с вырожденными уровнями энергии является электрон, движущийся под действием электрических сил при отсутствии магнитных взаимодействий, например, электрон в атоме водорода. В силу наличия у электрона спина уровни энергии электрона оказываются двукратно вырожденными.

При наличии дополнительных взаимодействий вырожденные уровни могут расщепляться: значения энергии для первоначально вырожденных состояний оказываются уже различными, и вырождение исчезает, или, как говорят, происходит снятие вырождения.

Например, для электронов в атоме Н двухкратное вырождение снимается при приложении внешнего магнитного поля. Направление маг. поля представляет выделенное направление, вдоль кот. ориентируется спин электрона, и энергия электрона уже будет зависеть от того, ориентирован ли спин параллельно или антипараллельно полю. Т. о. состояниям с параллельной и с антипараллельной ориентацией спина будут соответствовать уже различные уровни энергии.

ИТАК, Степень вырождения является весьма важной характеристикой уровней энергии.

Найдем степень вырождения уровней одноэлектронного атома. Степень вырождения определяется числом независимых состояний с данной энергией.

Рассмотрим сперва число независимых состояний при заданном значении квантового числа l.

При заданном мы имеем состояния, отличающихся значениями (из *). То есть вектор может быть ориентирован способами.

При заданных и возможны два состояния, отличающихся значениям . Всего при заданном l мы получаем - независимых состояний, т.е. степень вырождения по и уровня энергии с определенным l равна:

Теперь легко определить степени вырождения уровней с заданным главным квантовым числом n, если учесть, что при этом принимает значения от 0 до . Суммируя величину из (**) от 0 до получаем степень вырождения по n: