
Лекція 2.
Системи числення .Кодування інформації в ЕОМ
Будь-яке ненегативне число в позиційній системі числення (СС) може бути представлене у вигляді:
D = Cn-1*bn-1 + Cn-2*bn-2 + ... + C1*b1 + C0*b0 + C-1*b-1 + C-2*b-2 +..,
де D - десятковий еквівалент числа, Ci - значення i-го розряду, b - підстава системи счисления,b в ступені i - вага i-го розряду і n число розрядів цілої частини числа. У обчислювальній техніці найбільш поширені: двійкова (BIN), десяткова (DEC), шістнадцяткова (HEX) і непозиційна двійково-десяткова (BCD) системи числення. У BCD системі вага кожного розряду рівна ступені 10, як в десятковій системі, а кожна цифра i-го розряду кодується 4-мя двійковими цифрами. Вісімкова СС (OCT) застосовується рідше. Перші 16 чисел представлено в таблиці 1.
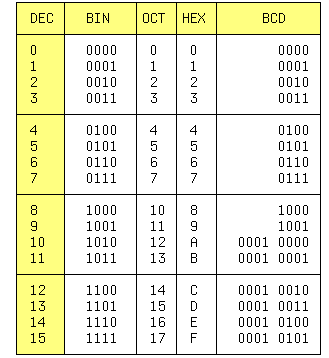
Двійкове число 10010011 = 1 * 2^7 + 1 * 2^4 + 1 * 2^1 + 1 * 2^0 = 147 (DEC). Для перекладу числа з двійкової системи в 16 - ную, його необхідно розбити починаючи справа на групи по 4 двійкових цифри і кожну групу представити 16 - ний цифрою з таблиці. Для зворотного перекладу кожна HEX цифра замінюється четвіркою двійкових, незначущі нулі зліва отб- расываются. Двійково-десяткове число можна записувати і десятковими цифрами, наприклад 1997, і двійковими - 0001 1001 1001 0111. Кожне десяткове число можна представити у вигляді BCD, наприклад 19(DEC)= 19(BCD), але їх двійкові уявлення не рівні: 19(DEC)= 10011(BIN), а 19(BCD)= 1 1001(BIN). Не кожен запис з нулів і одиниць має двійково-десятковий еквівалент. Наприклад, 11001001(BIN) = ?(BCD) = C9(HEX)= 201(DEC), оскільки десяткової цифри 12 = 1100 несуществует!
Машинне представлення інформації
Мікропроцесори обробляють впорядковані двійкові набори. Мінімальною одиницею інформації є один біт.

Далі слідують - тетрада (4 бита), байт ( byte 8 битий), подвійне слово (DoubleWord 16 битий) або довге (LongWord 16 битий) і збільшене учетверо слова. Молодший біт зазвичай займає крайню праву позицію.
Числа з фіксованою крапкою
Такі числа можуть бути як цілими, так і дробами. Крапка в думках фіксується поряд з будь-яким розрядом. Якщо вона розташовується праворуч від молодшого біта, то число ціле, якщо зліва від старшого - число дріб. Далі розглядатимуться тільки цілі числа з фіксованою крапкою, для нецілих чисел частіше застосовується показова форма, про яку піде мова далі.
Природним представленням цілого ненегативного числа є двійкова система числення. Кодування негативних чисел проводиться трьома найбільш споживаними способами, в кожному з яких крайній лівий біт - знаковий. Негативному числу відповідає одиничний біт, а позитивному - нульовий. Кожен спосіб оцінюється за швидкістю і витратам на виконання складання і зміни знаку числа, оскільки віднімання є складання із зміненим знаком одного операнда.
1.Прямий код. Зміна знаку проводиться просто, шляхом інверсії біта знаку. Хай 00001001 = 9, тоді 10001001 = -9. Якщо при складанні двох чисел в цьому коді знаки співпадають, то труднощів немає. Якщо знаки розрізняються необхідно знайти найбільше число, відняти з нього менше, а результату привласнити знак найбільшого доданку.
2.Обернений код, інверсний або додатковий "до 1". Зміна знаку проводиться просто - інверсією всіх біт: 00001001 = 9, а 11110110 = -9. Складання також виконується просто, оскільки знакові біти можна складати. При перенесенні одиниці з лівого (старшого) біта, вона повинна складатися з правим (молодшим). Наприклад: 7 + (-5) = 2.
00000111 = 7
11111010 =-5 (інверсія 00000101 = 5)
1 00000001
1
00000010 = 2
Складання в зворотному коді відбувається швидше, оскільки не потрібне ухвалення рішення, як у попередньому випадку. Проте підсумовування біта перенесення вимагає додаткових дій. Іншим недоліком цієї коди є представлення нуля двома способами, оскільки інверсія 0...00 рівна 1. ..11 і сума два разных по знаку, але рівних за значенням чисел дає 1...11.Например: (00001001 = 9) + (11110110 = -9) = 11111111. До речі, з цього прикладу зрозуміло чому код називається додатковим "до 1". Цих недоліків позбавлений ---
3.Додатковий або додатковий "до 2" код. Число з протилежним знаком знаходиться інверсією початкового і додаванням до результату одиниці. Наприклад, знайти код числа -9.
00001001 = 9 11110111 =-9
11110110 - інверсія 00001000 - інверсія
1 1
11110111 =-9 00001001 = 9
Проблеми двох нулів немає. +0 = 00000000 -0 = 11111111 + 1 = 00000000 (перенесення із старшого біта не враховується) .Додавання проводиться по звичайних для ненегативних чисел правилах.
00001001 = 9
11110111 =-9
1 00000000
З цього прикладу видно, що в кожному розряді двох рівних по модулю чисел складаються дві одиниці, що і визначило назву способу. Цей метод застосовується найчастіше, і коли говорять про додатковий код, то мається на увазі додатковий "до 2-х" код.
