14. Модель «хищник-жертва». Уравнения Лоттки-Вольтерра. Методы моделирования системы типа «хищник-жертва».

Система хищник-жертва - взаимосвязь между хищником и жертвой, в результате которой эволюционно выигрывают оба: хищники имеют корм, а популяции жертв избавляются от ослабленных членов. Система «хищник-жертва» — сложная экосистема, для которой реализованы долговременные отношения между видами хищника и жертвы, типичный пример коэволюции.

В "классическом" виде задача ставится следующим образом. Пусть имеются кролики, питающиеся травой (или морковью), при неограниченном ее количестве. Тогда при отсутствии хищников изменение численности R кроликов (R - rabbit) в зависимости от времени t описывается дифференциальным уравнением первого порядка:

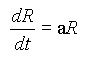(3.1)где a - коэффициент рождаемости. Это уравнение описывает неограниченный экспоненциальный рост численности популяции (т.н. закон Мальтуса, уравнение (1.2), рис. 1.1). Такой сценарий реализовался в Австралии в начальный период её "освоения" кроликами.

Пусть также имеются лисы, которые питаются только кроликами. Тогда, если кроликов нет, лисы вымрут, причем их численность F (F - fox) в зависимости от времени можно описать дифференциальным уравнением первого порядка:

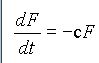(3.2)где c - смертность лис в единицу времени. Это уравнение описывает экспоненциальное сокращение численности популяции аналогично уравнению радиоактивного распада (см. уравнение (1.2), рис. 1.2).

Пустим козла в огород: пусть лисы и кролики проживают совместно. Кролики едят траву, размножаются, но не едят лис, в то время как лисы едят только кроликов, размножаются и умирают. Говорят, что кролики и лисы "взаимодействуют". При таком взаимодействии динамика популяции кроликов опишется:

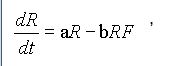где b - коэффициент гибели кроликов за счёт прожорливости лис.

Для популяции лис соответственно получаем:

где e - скорость роста популяции лис за счёт поедания кроликов.

Уравнения (3.3) и (3.4) называются уравнениями Лотки-Вольтерра и составляют систему из двух дифференциальных уравнений первого порядка с постоянными коэффициентами a,b,c,e. Из-за наличия перекрестных членов (bRF и cFR ) эта система является нелинейной.

Преобразуем уравнения системы к виду

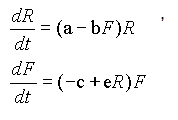(3.5)

В такой записи уравнения похожи на уравнения (3.1) и (3.2) , однако в отличии от них множители, стоящие в правых частях при R и F, не являются постоянными, а зависят от F и R соответственно. Если этот множитель больше 0, то будет наблюдаться рост переменной, если меньше 0 - уменьшение. Скорость этих изменений определяется не только постоянными параметрами, но и переменными R и F.

Таким образом, из-за взаимосвязанности уравнений системы поведение каждой переменной будет обнаруживать чередование роста и убывания, т.е. колебания. Эти колебания не являются гармоническими, причем колебания численности лис и кроликов сдвинуты друг относительно друга по фазе. Амплитуда колебаний в зависит от выбранных параметров и начальных условий.

Получение аналитического решения из-за нелинейности системы в общем случае невозможно. Ниже будет описано применение численных методов решения.

Методы решения дифференциальных уравнений

достаточно условно можно разбить на точные, приближенные и численные.

К точным относятся методы, позволяющие выразить решение дифференциального уравнения через элементарные функции (либо представить при помощи квадратур от элементарных функций). Однако классы уравнений, для которых разработаны методы получения точных решений, сравнительно узки и охватывают только малую часть возникающих на практике задач.

Приближенными называются методы, в которых решение получатся как предел некоторой последовательности, каждый член которой выражается через элементарные функции. Примером может служить разложение решения в обобщенный степенной ряд.

Численные методы - это алгоритмы вычисления приближенных значений искомого решения для дискретного набора значений аргумента. Численные методы не позволяют найти общего решения ДУ, и это является их основным недостатком. Зато эти методы применимы к очень широким классам уравнений. Поэтому с появлением быстродействующих компьютеров численные методы стали одним из основных способов решения конкретных практических задач.