9. Определение фрактала. Самоподобие, самоаффинность. Мера, размерности. (глава 5)

Геометрия Евклида оперирует простыми объектами и формами: точка, прямая линия, окружность, сфера, конус, цилиндр и т.п. Однако в природе эти формы почти не встречаются.

Даже такая простая и ясная в геометрии мера, как длина, становится вовсе не такой простой, когда мы начинаем измерять её у естественных объектов - например, у береговой линии. Линия эта не является прямой (и вообще ни одной из "евклидовых" линий) - значит, при измерении её надо разбить на участки, которые можно считать прямыми. Чем крупнее масштаб, тем больше точек - из-за извилистости (изрезанности) самой линии, - а, значит, и измеряемая длина. Таким образом, в природе длина объекта зависит от масштаба рассмотрения.

Для характеристики формы природных объектов Б.Мандельброт в 60-х годах ХХ-го столетия ввел понятие фрактальной (от латинского fractus - "дробный", и frahgere - "ломать") геометрии, определяя фрактал, как "структуру, состоящую из частей, которые в каком-то смысле подобны целому".

Это свойство самоподобия почти очевидно при рассмотрении береговой линии, речной сети, систем трещин и разломов, пористости в горных породах, форм геологических тел, различных биологических форм, кристаллов льда. Нельзя сказать, что береговая линия острова проще береговой линии континента, они, в определенном смысле, подобны. Можно обнаружить геометрическое подобие геологических объектов.

В качестве количественной меры структурности (формы) объектов Б.Мандельброт предложил использовать фрактальную размерность, показывающую, насколько плотно точки заполняют пространство. Фрактальная размерность позволяет количественно описывать неупорядоченные структуры.

фракталы - самоподобные объекты, характеризующиеся дробной размерностью.

Фракта́л (лат. fractus — дроблёный, сломанный, разбитый) — геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком.

Фракталы – геометрические объекты с дробной размерностью. К примеру, размерность линии – 1, площади – 2, объема – 3. У фрактала же значение размерности может быть между 1 и 2 или между 2 и 3. К примеру, фрактальная размерность скомканного бумажного шарика приблизительно равна 2,5. В математике существует специальная сложная формула для вычисления размерности фракталов. Разветвления трубочек трахей, листья на деревьях, вены в руке, река - это фракталы. Говоря простым языком, фрактал - это геометрическая фигура, определенная часть которой повторяется снова и снова, изменяясь в размерах - это и есть принцип самоподобия. Фракталы подобны самим себе, они похожи сами на себя на всех уровнях (т.е. в любом масштабе).

10. Методы измерения фрактальной размерности геометрических объектов. (глава 5)

До сих пор мы использовали понятие "размерность" в двух значениях:

(1) размерность Евклидова пространства (d = 1,2,3);

(2) количество переменных, описывающих в динамическую систему.

Ф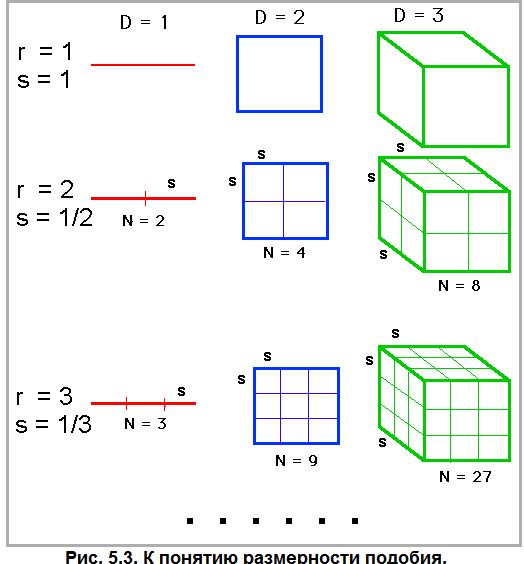 ракталы, которые являются нерегулярными геометрическими объектами, требуют расширения этого понятия. Понятие фрактальной размерности, или размерности подобия D. Рассмотрим объект (отрезок прямой, квадрат, куб) в Евклидовом пространстве, и уменьшим его линейный размер в r раз в каждом направлении. Затем подсчитаем количество N таких уменьшенных копий, необходимое для заполнения исходного объекта (или, что то же самое, будем измерять объект уменьшенной линейкой s=1/r). Самоподобие в этом случае носит тривиальный характер. Легко убедиться (рис. 5.3), что независимо от степени уменьшения r, будет выполняться соотношение

Определённая таким образом, размерность подобия D для компактных множеств, которыми оперирует геометрия Евклида, выражается целым числом (1,2,3), что совпадает с размерностью пространства d.

Существуют ли объекты, для которых размерность подобия выражается дробным числом? Оказывается, существуют - именно они и называются фракталами. На основании соотношения (5.1) было сформулировано обобщенное понятие фрактальной размерности как величины, которая не зависит от масштаба рассмотрения (измерения) и является характеристикой данного объекта. Прологарифмировав (5.1) , имеем

ln(N) = D ln (r), или получаем для D

Э та размерность носит название размерности Хаусдорфа - Безиковича.

Здесь используется ln - натуральный логарифм с основанием e»2.718281828, но вообще можно брать логарифм по любому основанию (например, десятичный lg) - т.к. в выражение входит их отношение, результат для D будет одинаковый.

Определённая таким образом размерность оказалось полезной при описании природных объектов и траекторий динамических систем.

Формула (5.2) позволяет определить размерность так называемых "регулярных" фракталов (они будут рассмотрены в разделе 5.3). Однако прямо применить её для природных объектов затруднительно.

Одним из методов исследования фрактальной размерности является клеточный метод.

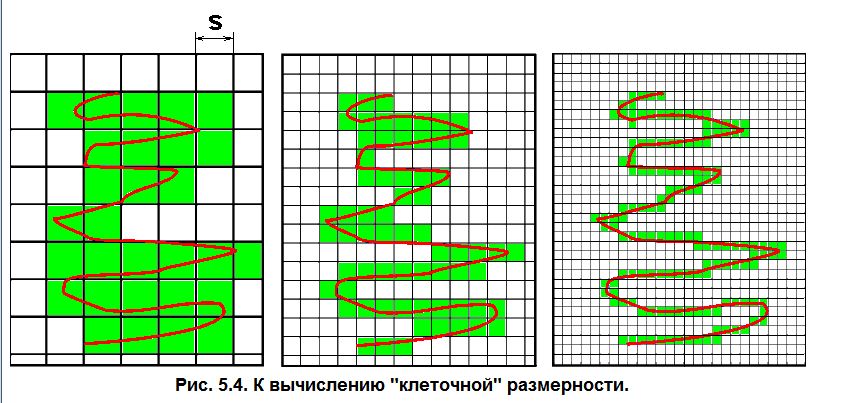
Он заключается в следующем. Исследуемый объект покрывается n-мерными кубиками со стороной, равной s, причём при каждом акте покрытия s изменяется. Пример такой процедуры приведён на рис.5.4, где плоская кривая последовательно покрывается квадратами с уменьшающимися сторонами (теоретически надо построить эту зависимость при s®0, но на практике всегда существуют ограничения на максимальный и минимальный размер клеток). Затем определяется число кубиков N, покрывающих множество, при различных значениях s. Далее устанавливается вид зависимости N=f(s). Если удаётся выделить область скейлинга (от scale), т.е. диапазон значений s, для которого зависимость имеет вид

то показатель степени является характеристикой размерности множества D. Чаще всего строят зависимость в двойном логарифмическом масштабе, т.е. вида ln(N) = f(ln (s)) (синие точки на рис.5.5). Затем область скейлинга аппроксимируется прямой линией (красный отрезок на рис.5.5), например, методом наименьших квадратов: ln(N) = - D ln (s) + a, (5.4) где a - постоянная. Тогда тангенс угла наклона графика является размерностью D (рис.5.5а).

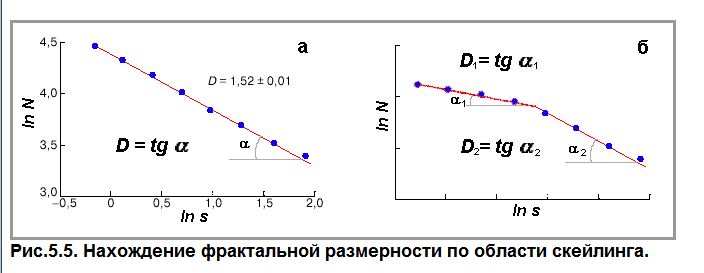
Во многих случаях наблюдаются изломы на графике зависимости ln(N) = f (ln (s)), что является свидетельством изменения структуры рассматриваемого множества. Тогда каждому участку соответствует своё значение размерности (рис.5.5б). далее идет в книге продолжение но оно относить ться к 13 вопросу.