Описание третьей подсистемы
Перемещаясь далее по вкладкам, пользователь может перейти к третьей подсистеме и оценить графическую интерпретацию спектральной плотности мощности случайного процесса, путем сравнения с теоретической
Рисунок 20 – Спектральная плотность мощности СП
Так как пользователь самостоятельно задает количество членов ряда, в третьей подсистеме можно посмотреть зависимость результатов от этой величины, путем наложения графиков, полученных при разных значениях параметра m (рисунок 21)
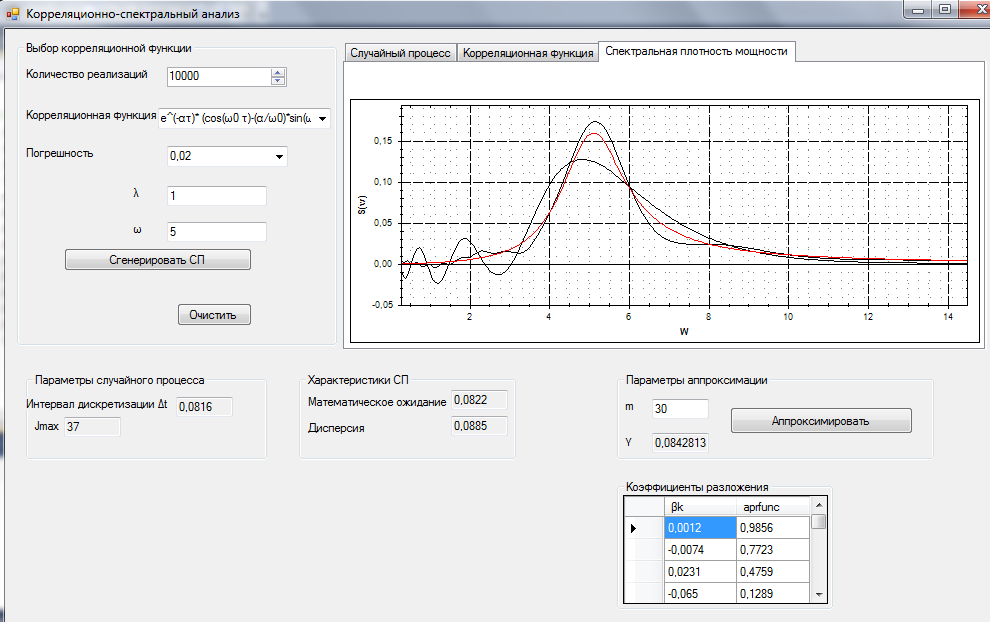
Рисунок 21 – Спектральные плотности мощности СП, при разных значениях параметра m
Выбор и обоснование конструкторско-технологических средств
Расчет требуемых ресурсов
Для того чтобы определить минимальные требования к системе необходимо произвести расчет используемой памяти
Расчет объема в оперативной памяти:
VОС= 256 Мб
VПС= 2,3 Мб
Vданных = 1 Мб
Vсправка = 11,5 Мб
Vозу =256 Мб + 2,3 Мб + 1Мб + 11,5 Мб = 270,8 Мб
Расчет объема на жестком диске:
VПС=9,25 Мб
Vсправка = 190 Кб
Vданных = 1 Мб
Vпр = 3 Мб
Vжд =9,25 Мб + 190 Кб + 1 Мб +3 Мб = 14.25 Мб
Минимальные требования к системе
На основании полученных требований к системе можно вывести минимальные требования необходимые для корректной работы системы.
IBM – совместимый компьютер с тактовой частотой процессора 300 МГц и более;
объем оперативной памяти не менее 256 Мб;
жесткий диск не менее 100 Мб;
монитор с разрешением 800x600;
ОС Microsoft Windows ХР/Vista/7 и совместимые.
Заключение
Была разработана система, которая позволяет моделировать и анализировать СП. При запуске система позволяет смоделировать СП. При моделировании СП пользователю необходимо выбрать вид корреляционной функции и задать ее параметры, После генерации СП, система рассчитывает числовые и вероятностные характеристики. Так же пользователь может построить ортогональную модель корреляционной функции в базисе Якоби [-1/2;0]. Результаты отображаются на форме в виде числовых значений и графиков.
При разработке пользовательского интерфейса были соблюдены основные требования. Система имеет дружелюбный, наглядный и интуитивно понятый пользователю интерфейс. В системе предусмотрена защита от ошибок неопытного пользователя.
В ходе разработки данного проекта были рассмотрены основы теории вероятности и технология RAD.
Список использованной литературы
Прохоров, С.А. Математическое описание и моделирование случайных процессов – Самара: СНЦ РАН,2001.-209с.
Определение технологии RAD [Электронный ресурс] http://www.informicus.ru/RAD
Прохоров, С.А. Аппроксимативный анализ случайных процессов – Самара: СНЦ РАН,2001.-380с.
СТО СГАУ 02068410-004-2007. Общие требования к учебным текстовым документам [Текст]: методические указания. Самара: Изд-во Самар. гос. аэрокосм. ун-та, 2007. 30с.
Прохоров, С.А. Ортогональные модели корреляционно-спектральных характеристик случайных процессов. Лабораторный практикум. – Самара: СНЦ РАН, 2008.-301с..
Прохоров, С.А. Прикладной анализ случайных процессов – Самара: СНЦ РАН,2007.-582с.
Прохоров, С.А., Куликовских, И.М. Справочник по основным ортогональным функциям и их приложениям.
Приложение А
Корреляционные функции
Название корреляционной функции |
Вид корреляционной функции |
Монотонные недифференцируемые |
|
Колебательные недифференцируемые |
e-α׀τ׀ *(cos(ω0τ) – α/ ω0*sin(ω0τ)); |
ПРИЛОЖЕНИЕ Б
Количество ординат КФ и интервалы дискретизации
Вид КФ |
Δt |
|
=0.05 |
||
Δt |
|
Δt |
|
||
|
|
|
9 |
|
6 |
e-α׀τ׀ *(cos(ω0τ) – α/ ω0*sin(ω0τ)) |
|
|
|
|
|
=0.02
ПРИЛОЖЕНИЕ В
Программная реализация системы
Класс Calculate – в котором производятся вычисления основных числовых характеристик: математического ожидания, дисперсии.
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace Khorova
{
class Calculate
{
public int quantityReadout; //количество отсчетов
public double digitizationInterval; //интервал дискретизации
public double[] values; //массив случайного процесса
public double[] valuesCentr; //центрированный массив случайного процесс
public double populationMean; //МО
public double dispersion; //дисперисия
public double[] correlationFunction; //КФ
public double gamma;
public double alfa;
public double omega;
public double[,] masFanction;
public double[] masBetta;
public double[] masBet;
public double[] teorCorrelationFunction;
public int Jmax;
public double[] massB;
public double[] masB;
public int order;
public double[] masDeltaM;
public Calculate(int n, double dt, double[] mas)
{
quantityReadout = n;
digitizationInterval = dt;
Jmax = 35;
values = mas;
populationMean = GetPopulationMean();
valuesCentr = GetCentrValues();
dispersion = GetDispersion();
correlationFunction = GetCorrelationFunction();
teorCorrelationFunction = GetTeorCorrelationFunction(50, gamma);
}
public Calculate(int n, double dt, double[] mas, int j, double t, double a, double w)
{
quantityReadout = n;
digitizationInterval = dt;
alfa = a;
omega = w;
gamma = 0.8 / digitizationInterval;//2*Math.Sqrt(Math.Pow(a,2)+Math.Pow(w,2));
Jmax = j;
values = mas;
populationMean = GetPopulationMean();
valuesCentr = GetCentrValues();
dispersion = GetDispersion();
correlationFunction = GetCorrelationFunction();
teorCorrelationFunction = GetTeorCorrelationFunction(50, gamma);
order = GetOrder(t);
}
public double GetPopulationMean() //метод возвращающий математическое ожидаение потока
{
double populationMean = values[0];
for (int i = 0; i < quantityReadout; i++)
populationMean += values[i];
populationMean = populationMean / quantityReadout;
return populationMean;
}
public double[] GetCentrValues() //метод возвращающий массив центрированных значений интервалов
{
double[] mas = new double[quantityReadout];
for (int i = 0; i < quantityReadout; i++)
{
mas[i] = values[i] - populationMean;
}
return mas;
}
public double GetDispersion() //метод возвращающий дисперсию
{
double dispersion = 0;
for (int i = 0; i < quantityReadout; i++)
dispersion += Math.Pow(valuesCentr[i], 2);
dispersion /= (quantityReadout - 1);
return dispersion;
}
private double[] GetCorrelationFunction()
{
double[] cF = new double[Jmax];
for (int i = 0; i < Jmax; i++)
{
for (int j = 0; j <= (quantityReadout - i - 1); j++)
cF[i] += ((values[j] - populationMean) * (values[j + i] - populationMean));
cF[i] = cF[i] / ((quantityReadout - i - 1) * dispersion);
}
return cF;
}
public double GetItemCorrelationFunction(int i)
{
return correlationFunction[i];
}
public double GetMaxArray() //метод возващающий максимум массива интервалов
{
double max = values[0];
for (int i = 1; i < quantityReadout; i++)
if (max < values[i])
max = values[i];
return max;
}
public double GetMinArray() //метод возвращающий минимум массива интервалов
{
double min = values[0];
int k = 0;
for (int i = 1; i < quantityReadout; i++)
if (min > values[i])
{
min = values[i];
k = i;
}
k++;
return min;
}
}
}
Класс Model1 – содержит в себе алгоритм рекурсивной фильтрации, с помощью которого получается СП с корреляционной функцией Rx(τ)= e-α׀τ׀ (модель 1), и вычисляется количество ординат для построения КФ.
sing System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace Khorova
{
class ModelFirst: SourceProcess
{
public ModelFirst(int n, double dt, double a, double w)
: base(n, dt, a, w)
{
}
public override double GetDigitizationInterval(double dt)
{
return (Math.Pow((8 * dt), 0.5) / alfa);
}
public override double[] GetMas()
{
double[] masY = new double[this.quantityReadout];
double gamma = alfa * digitizationInterval;
double p = Math.Pow(Math.E, ((-1) * gamma));
double a = Math.Pow((1 - Math.Pow(p, 2)), 0.5);
double b = p;
Random r = new Random();
for (int i = 0; i < this.quantityReadout; i++)
{
double x = r.NextDouble();
RecursiveFilter(i, a, b, x, masY);
}
return masY;
throw new NotImplementedException();
}
public void RecursiveFilter(int i, double a, double b, double x, double[] masY)
{
if (i == 0)
masY[i] = x;
else
masY[i] = a * x + b * masY[i - 1];
}
public override int GetJMax()
{
int j;
if (delta == 0.02)
j = 9;
else
j = 6;
return j;
}
public override double GetTay4()
{ double m;
m = 1 / (2 * alfa);
return m;
}
}
}
Класс Model2 - содержит в себе алгоритм рекурсивной фильтрации, с помощью которого получается СП с корреляционной функцией Rx(τ)= e-α׀τ׀*(1-ατ) (модель 2), и вычисляется количество ординат для построения КФ.
namespace Khorova
{
class Model2 : SourceProcess
{
public Model2(int n, double dt, double a, double w)
: base(n, dt, a, w)
{
}
public override double GetDigitizationInterval(double dt)
{
// определение интервала дискретизации
return (Math.Pow(8 * dt, 0.5) / alfa);
}
public override double[] GetMas()
{
double[] masY = new double[quantityReadout];
double[] masX = new double[quantityReadout];
double gamma = alfa * digitizationInterval;
double p = Math.Pow(Math.E, ((-1) * gamma));
double alfa0 = Math.Pow(p, 3) * (1 + gamma) - p * (1 - gamma);
double alfa1 = 1 - 4 * Math.Pow(p, 2) * gamma - Math.Pow(p, 4);
double a0 = Math.Pow(((alfa1 + Math.Pow((Math.Pow(alfa1, 2) - 4 * Math.Pow(alfa0, 2)), 0.5)) / 2), 0.5);
double a1 = alfa1 / a0;
double b1 = 2 * p;
double b2 = (-1) * Math.Pow(p, 2);
Random r = new Random();
for (int i = 0; i < this.quantityReadout; i++)
{
double x = r.NextDouble();
masX[i] = x;
RecursiveFilter(i, a0, a1, b1, b2, masX, masY);
}
return masY;
throw new NotImplementedException();
}
// алгоритм рекурсивной фильтрации
public void RecursiveFilter(int i, double a0, double a1, double b1, double b2, double[] masX, double[] masY)
{
if (i == 0)
masY[i] = masX[i];
else
{
if (i == 1)
masY[i] = a0 * masX[i] + a1 * masX[i - 1] + b1 * masY[i - 1];
else
masY[i] = a0 * masX[i] + a1 * masX[i - 1] + b1 * masY[i - 1] + b2 * masY[i - 2];
}
}
// определение количества ординат
public override int GetJMax()
{
int j = 13;
return j;
}
}
}
Класс Model7 - содержит в себе алгоритм рекурсивной фильтрации, с помощью которого получается СП с корреляционной функцией Rx(τ)= e-α׀τ׀ *(cos(ω0τ) – α/ ω0*sin(ω0τ)) (модель 7), и вычисляется количество ординат для построения КФ.
namespace Khorova
{
class Model7 : SourceProcess
{
public Model7(int n, double dt, double a, double w)
: base(n, dt, a, w)
{
}
// определение интервала дискретизации
public override double GetDigitizationInterval(double dt)
{
return (Math.Pow((8 * dt / Math.Abs(Math.Pow((omega / alfa), 2) - 1)), 0.5) / alfa);
}
public override double[] GetMas()
{
double[] masY = new double[quantityReadout];
double[] masX = new double[quantityReadout];
double gamma = alfa * digitizationInterval;
double p = Math.Pow(Math.E, ((-1) * gamma));
double gamma0 = omega * digitizationInterval;
double alfa0 = p * (Math.Pow(p, 2) - 1) * Math.Cos(gamma0) - (alfa / omega) * p * (Math.Pow(p, 2) + 1) * Math.Sin(gamma0);
double alfa1 = 1 - Math.Pow(p, 4) + 4 * Math.Pow(p, 2) * Math.Sin(gamma0) * Math.Cos(gamma0) * (alfa / omega);
double a0 = Math.Pow(((alfa1 + Math.Pow((Math.Pow(alfa1, 2) - 4 * Math.Pow(alfa0, 2)), 0.5)) / 2), 0.5);
double a1 = alfa0 / a0;
double b1 = 2 * p * Math.Cos(gamma0);
double b2 = (-1) * Math.Pow(p, 2);
Random r = new Random();
for (int i = 0; i < this.quantityReadout; i++)
{
double x = r.NextDouble();
masX[i] = x;
RecursiveFilter(i, a0, a1, b1, b2, masX, masY);
}
return masY;
throw new NotImplementedException();
}
// алгоритм рекурсивной фильтрации
public void RecursiveFilter(int i, double a0, double a1, double b1, double b2, double[] masX, double[] masY)
{
if (i == 0)
masY[i] = masX[i];
else
{
if (i == 1)
masY[i] = a0 * masX[i] + a1 * masX[i - 1] + b1 * masY[i - 1];
else
masY[i] = a0 * masX[i] + a1 * masX[i - 1] + b1 * masY[i - 1] + b2 * masY[i - 2];
}
}
public override int GetJMax()
{
int j = (int)Math.Round(47 * (omega) / (2 * Math.PI));
return j;
}
}
}
Класс SourseProcess
sing System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace Khorova
{
abstract class SourceProcess
{
public Calculate calculatCharacter;
public int quantityReadout; //количество отсчетов
public double digitizationInterval; //интервал дискретизации
public double[] values; //массив случайного процесса
public double alfa;
public double omega;
public double delta;
public double tay;
public SourceProcess(int n, double dt, double a, double w)
{
quantityReadout = n;
alfa = a;
omega = w;
delta = dt;
tay = GetTay4();
digitizationInterval = GetDigitizationInterval(dt);
int j = GetJMax();
values = GetMas();
calculatCharacter = new Calculate(n, digitizationInterval, values, j, tay,a,w);
}
public abstract double[] GetMas();
public abstract double GetDigitizationInterval(double dt);
public abstract int GetJMax();
public abstract double GetTay4();
}
}
// ОПИСАНИЕ ЯКОБИ (-1/2 0)
double[,] masYakobi = new double[KolChR, c.Jmax];
for (int i = 0; i < KolChR; i ++)
for (int j = 0; j < c.Jmax; j++)
{
double tay = j * c.digitizationInterval;
if (i == 0)
masYakobi[i, j] = Math.Exp(-1 * gamma * tay / 2);
else
if (i == 1)
masYakobi[i, j] = Math.Exp(-1 * gamma * tay / 2) * (1 - 3 * Math.Exp(-2 * gamma * tay)) / 2;
else
{
int z = 4 * i - 5;
int x = 4 * i - 1;
int b = 2 * i - 1;
int r = 4 * i - 3;
int t = 2 * i - 3;
int y = i - 1;
masYakobi[i, j] = ((z * x * (1 - 2 * Math.Exp(-2 * gamma * tay)) + 1) * r * masYakobi[i - 1, j] - 4 * y * t * x * masYakobi[i - 2, j]) / (4 * i * b * z);
}
}
//ОПИСАНИЕ 1ГО ИНТЕГРАЛА
double[,] masI1 = new double[KolChR, c.Jmax];
for (int i = 0; i < KolChR; i++)
{
for (int j = 0; j < c.Jmax; j += 1)
{
double tay = j * c.digitizationInterval;
if (i==0)
masI1[0, j] = -2* Math.Exp(-gamma*tay/2)/gamma;
else
if (i==1)
masI1[i, j] = (-1 * Math.Exp(-gamma * tay / 2) * (5 - 3 * Math.Exp(-2*gamma*tay)))/ (5*gamma);
else
{
double ch = (4 * i + 1);
double ch2 = 4 * i - 3;
double ch3 = 4 * i - 7;
masI1[i, j] = (2 * ch2 * masI1[i - 1, j]) / ch - (ch3 * masI1[i - 2, j]) / ch - 2 * ((masYakobi[i, j] - masYakobi[i - 2, j]) ) / (gamma * ch);
}
}
}
// ОПИСАНИЕ 2ГО ИНТЕГРАЛА
double[,] masI2 = new double[KolChR, c.Jmax];
for (int i = 0; i < KolChR; i++)
{
for (int j = 0; j < c.Jmax; j ++)
{
double tau = j * c.digitizationInterval;
double ex = Math.Exp((- gamma * tau) / 2);
double ex2 = Math.Exp(-2 * gamma * tau);
double ex3 = Math.Exp(-4 * gamma * tau);
if (i == 0)
masI2[i, j] = (-2 * ex * (gamma * tau + 2)) / (Math.Pow(gamma, 2));
else
if (i == 1)
masI2[i, j] = -1 * ex * (50 - 6 * ex2 + gamma * tau * (25 - 15 * ex2)) / (25 * Math.Pow(gamma, 2));
else
if (i==2)
masI2[i, j] = -1 * ex * (2430 - 972 * ex2 + 350 * ex3 + gamma * tau * (1215 - 2430 * ex2 + 1575 * ex3)) / (1620 * Math.Pow(gamma, 2));
else
{
double ch = (4 * i + 1);
double ch2 = 4 * i - 3;
double ch3 = 4 * i - 7;
masI2[i, j] = (2 * ch2 * masI2[i - 1, j]) / ch - (ch3 * masI2[i - 2, j]) / ch - 2 * ((masYakobi[i, j] - masYakobi[i - 2, j]) * tau - masI1[i, j] + masI1[i - 2, j]) / (gamma * ch);
}
}
}
// ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ РАЗЛОЖЕНИЯ
double[] masTau = new double [c.Jmax];
double[] A = new double[c.Jmax ];
double[] B = new double[c.Jmax ];
double[] Betta = new double[KolChR ];
double summaB=0;
for (int q = 0; q < c.Jmax; q ++)
{
masTau[q] = q * c.digitizationInterval;
}
for (int q = 0; q < c.Jmax -1 ; q += 1)
{
A[q] = (c.correlationFunction[q + 1] - c.correlationFunction[q]) / (masTau[q + 1] - masTau[q]);
// A[q] = (TeorCorFuncM7(masTau[q + 1]) - TeorCorFuncM7(masTau[q])) / (masTau[q + 1] - masTau[q]);
}
for (int q = 0; q < c.Jmax; q ++)
{
B[q] = c.correlationFunction[q] - A[q] * masTau[q];
}
// коэффициенты bk
for (int k = 0; k < KolChR; k += 1)
{
for (int j = 0; j < c.Jmax-1; j += 1)
{
summaB = summaB + B[j] * (masI1[k, j + 1] - masI1[k, j]) + (A[j] * (masI2[k, j + 1] - masI2[k, j]));
}
Betta[k] = gamma * (4 * k + 1) * summaB;
summaB = 0;
}
//аппроксимация
double[] masAprFunc = new double[c.Jmax];
for (int q = 0; q < c.Jmax ; q++)
{
for (int i = 0; i < KolChR; i++)
{
masAprFunc[q] += Betta[i] * masYakobi[i, q];
}
}
// практический спектр
private double AprSpektr(double w, double [] BettaK)
{
double g = Convert.ToDouble(textBoxGammaOpt.Text);
double sum = 0;
double spektr = 0;
double arctg, REZ;
KolChR = Convert.ToInt16(textBoxKolChR.Text);
for (int k = 0; k < KolChR; k++)
{
sum = 0;
for (int s = 0; s < k; s++)
sum += Math.Atan(2 * w / (g * (4 * s + 1)));
arctg = Math.Atan(2 * w / (g * (4 * k + 1)));
spektr += BettaK[k] * Math.Cos(arctg) * Math.Cos(arctg + 2 * sum)/(4*k+1);
}
REZ = (2 * spektr / (g * Math.PI));
spektr = 0;
return REZ;
}