Отсюда нетрудно вычислить высоту сферического сегмента

h_m= .

Пренебрегая слагаемым, содержащим λ², получим:

h_m= 7.5

Площади сферических сегментов:

S_m=2πah= ,

S_m-1=

Теперь ясно, что площадь m-ой кольцевой зоны Френеля

∆S_m=S_m-S_m-1= . 7.6

Полученный результат свидетельствует о том, что площадь зоны не зависит от её номера -m. Это означает, что площади зон Френеля приблизительно одинаковы.

Попутно отметим, что из уравнения (7.4) можно получить выражение для радиуса m-ой зоны

r_m= 7.7

Вернёмся к интегралу Френеля (уравнение 7.2)

E_P=

Рассмотрим его отдельно для каждой из зон. С ростом номера, как было показано, площадь зоны не меняется, но растёт расстояние r_m=b+m и уменьшается коэффициент k(φ) (с увеличением φ). В результате, с ростом номера зоны амплитуды соответствующих колебаний в точке P будут монотонно убывать:

E₁>E₂>E₃>…>…

Учитывая, что колебания от двух соседних зон происходят в противофазе, амплитуду результирующего колебания можно представить в виде:

E_P= E₁-E₂+E₃-E₄+…

Или так:

E_P= 7.8

Амплитуды с ростом номера зоны монотонно убывают, поэтому можно принять, что E_m= . Отсюда следует, что все скобки в выражении (7.8) равны нулю.

Амплитуда колебания, создаваемого в точке P всеми вторичными источниками сферической волновой поверхности:

E=

Эта амплитуда вдвое меньше амплитуды того колебания, которое создаётся в точке P вторичными источниками только одной первой зоны (!). Если открыта не вся волновая поверхность, а только m зон, то результирующая амплитуда:

E_P= при чётном m и

E_P= при нечётном m.

Более детально эту задачу можно решить, воспользовавшись методом векторных диаграмм

Разобьём зоны Френеля на сферической волновой поверхности на большое число «подзон». Каждая зона Френеля, таким образом, будет разделена на большое число элементарных кольцевых подзон. В точке наблюдения эти подзоны будут создавать колебания, сдвинутых по фазе на малую долю π. Сложим эти колебания, используя метод векторных диаграмм (рис.7.7)

Рис.7.7

На рис.7.7 модуль каждого вектора равен амплитуде колебаний в точке P от соответствующей подзоны. И каждый вектор повёрнут относительно предыдущего на угол, равный разности фаз этих соседних колебаний.

Учитывая, что с ростом номера подзоны амплитуда колебаний падает, в результате сложения колебаний получим не замкнутую линию, а ломаную спираль. При увеличении числа подзон и, соответственно, уменьшении их площади, ломаная спираль будет стремиться к гладкой (рис.7.8).

Рис.7.8

4. Дифракция от круглого отверстия.

Поставим на пути SP непрозрачную преграду с вмонтированной диафрагмой (рис.7.9). Открывая диафрагму, т. е. увеличивая радиус отверстия r₀, мы тем самым сможем последовательно открывать области первой зоны, затем второй, третьей и т.д.

Рис.7.9

На рис.7.10 представлены амплитуды колебаний от зон, которые последовательно открываются по мере увеличения отверстия диафрагмы.

Рис.7.10

O1 – амплитуда колебаний от первой зоны,

12 – от второй,

OC –амплитуда колебаний, приходящих от полностью открытой волновой поверхности. Видно, что

ОC=A_P=

Вектор OB соответствует амплитуде колебаний, приходящих в точку P только от внутренней половины первой зоны Френеля.

5. Зонные пластинки. Фокусировка.

Открывая постепенно диафрагму, можно наблюдать в точке P рост результирующего колебания. Этот рост закончится, когда диафрагма целиком откроет первую зону (E₁).

При дальнейшем увеличении диафрагмы начнут открываться области второй зоны. Результирующая амплитуда в точке наблюдения начнёт уменьшаться. Она станет почти нулевой, когда окажутся открытыми первые две зоны Френеля.

Затем вновь начнётся рост амплитуды: открывается третья зона. Открытие четвёртой зоны ознаменуется снижением амплитуды. Таким образом, каждая чётная зона «гасит» волну от предыдущей нечётной.

На рис. 7.11 приведена векторная диаграмма для случая, когда чётные зоны отсутствуют. Как это можно сделать? Для этого надо изготовить такую преграду-маску, которая закрывала бы чётные зоны но оставалась бы прозрачной для нечётных (рис.7.12).

Рис.7.11 Рис.7.12

Амплитуда колебаний в точке P в этом случае резко возрастёт (см. рис.7.11). Это результат того, что удалось исключить гасящее влияние чётных зон.

Можно создать преграду, прозрачную для всех зон, но такой формы, чтобы оптический ход волны от каждой чётной зоны оказался бы на λ больше оптического хода волны от предыдущей нечётной зоны (рис. 7.13).

а

в

Рис.7.13 Рис.7.14

В этом случае чётные зоны не исключаются. Их фаза увеличивается на π, и они создают в точке наблюдения колебания, синфазные с колебаниями нечётных зон.

Соответствующая векторная диаграмма представлена на рис. 7.14а.

Ну и, наконец, можно ведь создать зонную пластинку более тонкой структуры. Пластинку, влияющую не на целые зоны, а только на подзоны. Это означает, что следует ступенчатую зонную пластинку заменить собирающей линзой. Эффект ее действия представлен на векторной диаграмме 7.14в.

Лекция 9

<<Дифракционная решётка как спектральный прибор>>

План лекции:

1. Краткий обзор предыдущих лекций.

1.1 Критерий типа дифракции.

1.2 Дифракция Фраунгофера от щели.

1.3 Многолучевая интерференция.

2. Дифракционная решётка как спектральный прибор.

3. Критерий Рэлея. Разрешающая способность дифракционной решётки.

1. Краткий обзор предыдущих лекций.

Дифракционная решётка представляет собой совокупность большого числа одинаковых, равностоящих параллельных щелей. Изготавливают решётки, нанося с помощью делительной машины штрихи на плоскую стеклянную или металлическую поверхность. Разные решётки содержат разное число штрихов на каждый миллиметр: от десятков до десятка тысяч. На рисунке (9.1) представлен фрагмент одномерной дифракционной решётки.

b

Рис.9.1

Здесь b – ширина щели, d – расстояние между щелями. Это расстояние называется «постоянная решётки» (период). Речь здесь идёт, конечно, о пространственной периодичности, но не о временной.

Теперь рассмотрим плоскую световую волну, падающую на дифракционную решётку.

Свет будет дифрагировать на каждой щели. Далее за решёткой волны, идущие от всех щелей, при наложении интерферируют.

Таким образом мы встречаемся с двумя задачами, каждую из которых мы ранее подробно рассматривали.

Это: 1 – дифракции Фраунгофера на щели и

2 – многолучевая интерференция.

Освежим в памяти выводы, к которым мы пришли, решая эти задачи.

1. Критерии типа дифракции (см. лекцию №8)

Различают два типа дифракции:

Дифракцию сферических волн, или дифракцию Френеля и

дифракцию плоских волн – дифракцию Фраунгофера.

На прошлой лекции был получен безразмерный численный параметр, определяющий тип дифракции от щели: .

Было показано, что если этот параметр многим меньше единицы, наблюдается дифракция Фраунгофера. Когда он порядка единицы, – дифракция Френеля.

<<1 – дифракция Фраунгофера.

~1 - дифракция Френеля.

Мы будем изучать работу дифракционной решётки при условии дифракции Фраунгофера.

1.2 Дифракция Фраунгофера от щели (см. лекцию №8)

При дифракции Фраунгофера от щели “b” на экране наблюдения возникает дифракционная картина (рис. 9.2) чередующихся максимумов и минимумов.

Рис. 9.2

Было установлено, что интенсивность света является функцией угла дифракции φ:

(9.1)

Отсюда нетрудно получить условия минимумов:

b sin φ= ±k λ (k=1,2,3.....) ..................................................(9.2)

2. Многолучевая интерференция (см. лекцию №6)

Складывая когерентные волны, излучаемые равноотстоящими точечными синфазными источниками (рис.9.3), мы получим закон распределения интенсивности в дальней волновой зоне:

(9.3)

Здесь Ip – результирующая интенсивность в направлении ,

I1 – интенсивность в точке наблюдения от одного источника,

N – число источников.

Анализ уравнения (9.3) позволил выявить направления , в которых результирующая интенсивность принимает максимальное значение. Это так называемое условие максимумов:

sin Ө_max= ±m λ/d, m=0,1,2,.......................................(9.4)

Здесь λ – длина волны излучения,

d – расстояние между источниками.

2. Дифракционная решётка как спектральный прибор.

Пусть на решётку падает нормально плоская монохроматическая волна (λ). С тем, чтобы оставаться в рамках дифракции Фраунгофера, за решёткой поместим собирающую линзу, а в её фокальной плоскости – экран наблюдения (рис.9.3). Рис.9.3

Ясно, что распределение интенсивности на экране от одной щели будет определятся только направлением дифрагировавших лучей. Это означает, что дифракционные картины, создаваемые на экране любой отдельной щелью, будут совершенно одинаковы, независимо от положения щели на решётке (см. 9.1).

Теперь сложим N таких волн, дифрагировавших на щелях решётки. Результат сложения двух волн, пришедших через соседние щели, будет определятся разностью хода Δ=dsinφ. Суммарную интенсивность, возникшую от сложения N подобных волн, запишем в виде уравнения (9.3):

, (9.5)

где ε=kdsinφ – разность фаз волн, приходящих от двух соседних щелей

О бъединив выражение (9.1) и (9.5), получим окончательное распределение интенсивности света за дифракционной решёткой.

(9.6)

Здесь I0 – интенсивность, создаваемая одной щелью против центра линзы,

b – ширина щели,

N – число щелей,

d – период (постоянная) решётки.

Проанализируем полученный результат (9.6)

1. Интенсивность обращается в ноль, когда bsinφ=±kλ (k=1,2,3...) .................................(9.7)

Это известное условие минимума при дифракции от щели(9.2).

2.В направлениях φ, удовлетворяющих условию

dsinφ=±mλ (m=0,1,2,3...), .........................................................................................(9.8)

будут наблюдаться главные интерференционные максимумы при наложении N волн. Это условие максимумов многолучевой интерференции (см. (9.4)). В этих направлениях волны от всех N щелей решетки приходят к точке наблюдения в фазе, поэтому их амплитуды складываются. Результирующая амплитуда: Aрез = NAφ.

Интенсивность пропорциональна квадрату амплитуды, поэтому

(9.9)

Здесь Iщ(φ) – интенсивность света, дифрагировавшего от одной щели в направлении φ.

Между двумя соседними главными максимумами располагаются (N – 1) промежуточный минимум. Эти минимумы делят расстояние между главными максимумами на N частей. Картина распределения интенсивности за дифракционной решёткой для N = 4 и (d/b) = 3, приведена на рис. 9.4. Пунктирная кривая изображает здесь интенсивность от одной щели, умноженнуя на N².

Рис.9.4

Число главных максимумов вытекает из (9.8):

Угол между направлениями на два минимума, ограничивающих главный максимум, называется угловой шириной максимума.

Подсчитаем, например, угловую ширину нулевого максимума (см.рис. 9.4)

(9.10)

Дифракционные решётки широко используются в качестве спектральных приборов благодаря тому, что положение главных максимумов за решёткой зависит от длины волны λ:

(9.11)

Если на решётку падает смесь двух волн: λ и (λ+ δ λ), то их нулевые максимумы, конечно, совпадут, но m-ые максимумы окажутся в разных точках экрана.

Условие m-го максимума волны λ: sinφ_m=m(λ/d)

волны (λ+ δ λ): sinφ_m=m(λ+ δ λ)/d

Таким образом появляется возможность разложить с помощью дифракционной решётки смесь волн в спектр и измерить длины волн, входящих в смесь, либо их частоты.

2. Критерий Рэлея. Разрешающая сила дифракционной решётки.

Одной из основных характеристик спектрального прибора (будь то дифракционная решётка или призма) является его разрешающая сила. Разрешающая сила спектрального прибора определяется безразмерной величиной

R= λ/ δλ…………..(9.12)

Здесь δλ – минимальная разность длин волн двух спектральных линий, при которой спектральный аппарат разрешает эти линии, т.е. позволяет их рассмотреть на экране наблюдения раздельно.

Выясним, от чего зависит разрешающая сила дифракционной решётки.

Согласно критерию Рэлея спектральные линии с длинами волн λ и λ’= λ+ δλ будут разрешены, если главный максимум для одной длины волны совпадает с первым дифракционным минимумом в том же порядке для другой длины волны (рис. 9.7).

Условие m-го максимума для волны λ’= λ+ δλ: d sin φ_max=m(λ+ δλ)…………………(9.13)

Условие первого минимума, ограничивающего m-ый максимум волны λ:

d sin φ_min=(m+1/N) λ……………………………………………………………………..(9.14)

В случае минимальной разности длин волн δλ условия (9.13) и (9.14) описывают одну и ту же точку экрана, т.е. d sin φ_max=dsin φ_min

Иными словами, условие Рэлея позволяет записать следующее равенство:

m(λ+ δλ)=(m+1/N) λ или m δλ= λ/N

Отсюда следует, что разрешающая сила дифракционной решётки зависит только от числа её щелей (N) и от номера (m) спектра, в котором разрешаются спектральные линии.

R= λ/ δλ=mN................................................................................(9.15)

Лекция 10.

Экспериментальные основы квантовой механики.

План лекций.

1. Равновесное тепловое излучение.

   1. Тепловое излучение абсолютно черного тела.

   2. Классические теории Вина и Рэлея-Джинса. «Ультрафиолетовая катастрофа»

   3. Гипотеза Планка.

2. Фотоэффект. Уравнение Эйнштейна.

   1. Опыты Столетова.

   2. Уравнение Эйнштейна для внешнего фотоэффекта.

К концу 19 века успехи классической механики и классической электродинамики были ошеломляющими. Казалось, что область применяемости этих двух теорий безгранична.

На безоблачном горизонте физики оставалось только несколько легких облачков – нерешенных задач. Среди них – особенности теплового излучения черных тел, свойства фотоэффекта. Ждали своего объяснения и закономерности атомных спектров…

Никто не сомневался, что эти загадки природы будут решены в ближайшее время. Однако для решения этих задач пришлось создать принципиально новую физику – квантовую механику.

1. Равновесное теплового излучения.

Тепловое излучение – это испускание электромагнитных волн за счет внутренней энергии излучающих тел. Количественно этот процесс характеризуется энергетической светимостью, т.е. энергией, излучаемой в единицу времени единичной поверхностью излучающего тела. Энергетическую светимость измеряют в .

Тепловое излучение происходит в широком диапазоне частот электромагнитных волн.

Энергия, излучаемая в диапазоне частот от до , пропорциональна ширине диапазона :

Здесь - испускательная способность тела.

При заданной неизменной температуре Т, энергетическую светимость тела легко связать с его испускательной способностью

Подобно испускательной способности, вводиться понятие поглощательная способность тела

В этом определении – поток лучистой энергии, падающий на элементарную площадку dS поверхности тела (рис.10.1). Эта энергия принесена электромагнитными волнами в диапазоне частот от до

Часть этого потока отражается, а другая часть – поглотиться поверхностью.

Поглощательная способность , также как и излучательная – , является функцией температуры тела и частоты излучения.

Тела, поглощающие всё падающее на них излучение, называются абсолютно черными. Поглощательная способность таких тел равна,

Рис.10.1

конечно, единице

Термин «абсолютно черное тело» ввел в 1860 году Кирхгоф. Он же, исходя из термодинамических соображений, установил, что в условиях термодинамического равновесия такое тело излучает столько же энергии, сколько и поглощает.

При этом отношение испускательной и поглощательной способностей тела не зависит от его природы и является для всех тел одной и той же функцией частоты и температуры (закон Кирхгофа).

Поскольку поглощательная способность абсолютно черного тела равна единице ( ), универсальная функция Кирхгофа совпадает с излучательной способностью такого тела.

Однако в природе не встречаются абсолютно черные тела. Даже сажа отражает некоторую часть падающего на неё излучения.

Удовлетворительной моделью абсолютно черного тела считается небольшое отверстие в полом предмете (рис.10.2). Внутреннюю поверхность такого предмета нужно выкрасить в черный цвет. Излучение, падающее на поверхность отверстия, проникает в полость и в результате многократных отражений фактически нацело поглощается.

Многие ученые в начале прошлого века экспериментально исследовали тепловое излучение абсолютно черных тел.

Опыты Люммера в видимой части излучения, Бекмана и Пашена – в инфракрасной области, опыты Байша - в ультрафиолетовой позволили

Рис.10.2

установить универсальную функцию Киргофа при разных температурах и в разных областях излучаемого спектра.

Экспериментальные кривые излучательной способности абсолютно черного тела при разных температурах приведены на рис.10.3.

О брабатывая эти экспериментальные результаты, профессор Венского университета Иозеф Стефан установил, что интегральная светимость абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры.

Годом позже другой венский физик – Людвиг Больцман – доказал, что закон Стефана есть прямое следствие законов в классической термодинамики.

Закон Стефана-Больцмана:

Как следует из графиков рис 10.3, с повышением температуры абсолютно черного тела, максимум излучательной способности смещается в область более коротких волн (высоких частот).

Эту закономерность излучения черного тела Вильгельм Вин

Рис.10.3

сформулировал в виде следующего закона:

Произведение абсолютной температуры черного тела на длину волны, соответствующую максимуму излучения, постоянно

(Закон смещения Вина)

Таковы основные закономерности излучения абсолютно черного тела, экспериментально установленные в начале прошлого века.

2. Классические теории Вина и Рэлея-Джинса. «Ультрафиолетовая катастрофа».

Особенности излучения черного тела многие ученые пытались объяснить с позиций классической термодинамики. Опираясь на законы термодинамики, принцип равного распределения энергии по степеням свободы, применяя методы классической статической механики для стационарных волн, которые могли бы существовать в полости, Вин, Рэлей Джинс и многие другие ученые пытались получить теоретическую формулу, описывающую известную экспериментальную функцию

Однако формула, например, полученная Вином, неплохо совпадающая с экспериментальными данными в высокочастотной области излучения, расходилась с экспериментом в низкочастотной части спектра.

Формула Рэлея-Джинса, напротив, подтверждалась в низкочастотной части спектра и уводила в бесконечность в высокочастотной области (рис10.4)

Рис.10.4

Энергетическая светимость тела, вычисленная с использованием теоретической формулы Рэлея-Джинса, оказывается бесконечной.

Отсюда следует абсурдный вывод:

плотность энергии в равновесной системе бесконечна!

Этот результат, получивший название ультрафиолетовой катастрофы, на самом деле означал катастрофу классической физики.

2. Гипотеза Планка.

В 1889 году к теоретическому изучению излучения черного тела приступил Макс Планк. Ему удалось подобрать такую эмпирическую формулу, которая приводила к формуле Вина в области коротких волн и совпадала с законом Рэлея-Джинса в длинноволновой области.

Формула Планка позволяет вычислить интегральную светимость абсолютно черного тела. Это вычисление приводит к закону Стефана-Больцмана.

При этом постоянная Больцмана - σ, рассчитанная по формуле Планка, в точности совпадает с тем значением, которое дает эксперимент.

Формула Планка подтверждает и закон смещения Вина

И здесь постоянная “b” подтверждается экспериментом.

Найдя столь удачную формулу, Планк попытался объяснить физический смысл новой константы , которую ему пришлось ввести в это математическое выражение.

Оказалось, что формула безукоризненно описывает излучение черного тела только в предположении, что каждый колеблющийся осциллятор, окруженный абсолютно поглощающей оболочкой, излучает энергию дискретно, то есть порциями – квантами.

Энергия такого кванта по Планку пропорциональна частоте:

Если согласиться с этой неслыханной гипотезой о порциальном излучении энергии, возникает новый вопрос: Каков механизм распространения этих “порций энергии”?

Сохраняют ли кванты свою индивидуальность или каждый элемент рассеивается в пространстве, превращаясь в электромагнитную волну?

Первое предположение – об индивидуальности квантов - несовместимо с классической волновой теорией оптики и теплового излучения.

Опасаясь отбрасывать волновую теорию, которая на протяжении целого века ни у кого не вызывала никаких сомнений, Планк избрал второе из двух объяснений. В первоначальной формуле его теория предполагала испускание излучения дискретным, в виде квантов, а само излучение – непрерывным.

«Когда думаешь о полном опытном подтверждении, которое получила электродинамика Максвелла, - писал Планк в 1911 году, - о необычайных трудностях, с которыми придется столкнуться всем теориям при объяснении электрических и магнитных явлений, если они откажутся от этой электродинамики, инстинктивно испытываешь неприязнь ко всякой попытке поколебать её фундамент».

2. Фотоэффект. Уравнение Эйнштейна.

Фотоэффект – явление испускания электронов проводником при его облучении – был открыт в конце 19 столетия. Почти одновременно – в 1887-1890 годах – это явление наблюдали Шустер, Герц, Галльвакс, Риги другие исследователи.

Итальянский ученный А. Риги так формулирует суть эффекта:

«Излучения, действуя на металлы, электризуют их положительно» (рис.10.5).

Рис.10.5

Первые фундаментальные исследования фотоэффекта были проведены в лаборатории российского ученого А.Г.Столетова.

2.1 Опыты Столетова.

Принципиальная схема установки Столетова представлена на рис10.6.

З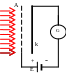 десь на два электрода – катод (К) и анод (А) – подается постоянное напряжение от источника (Е). Анод выполнен в виде металлической сетки, сквозь которую катод освещается монохроматическим светом.

При освещении катода в цепи возникает электрический ток, который регистрировался чувственным гальванометром (G).

Меняя частоту и интенсивность света, падающего на фотокатод, Столетов экспериментально установил, что сила тока, возникающего под действием света, пропорциональна его интенсивности, то есть

Рис.10.6

освещённости фотокатода. Кроме того, было обнаружено, что не всякое излучение приводит к возникновению фототока. Наибольшей эффективностью обладает коротковолновое (ультрафиолетовое) излучение.

2.2. Эксперименты Ленарда и Томсона.

Одновременно с работой А.Г.Столетова проводилось тщательное исследование фотоэффекта американскими учёными Ленардом и Томсоном. В их экспериментальной установке электроды были помещены в глубоко вакуумированный сосуд. Свет на катод падал через специальное окошко, закрытое кварцевым стеклом. Анодное напряжение менялось здесь не только по величине, но могло быть изменено и по знаку.

На рисунке 10.7 представлена принципиальная схема экспериментальной установки Ленарда-Томсона.

Рис.10.7 Здесь можно было менять:

1.частоту падающего излучения,

2.интенсивность излучения,

3.анодное напряжение.

На рисунке 10.8 приведена типичная вольт-амперная характеристика фотоэлемента: зависимость фототока от величины анодного напряжения.

При этом частота и интенсивность излучения, падающего на катод, остаются постоянными.

Отметим главные особенности этой характеристики:

1.наличие тока насыщения (I_s),

2.анодный ток в цепи не равен нулю, даже при отсутствии разности потенциалов между анодом и катодом,

Рис.10.8 3.для прекращения фототока, необходимо на анод подать отрицательный потенциал относительно катода - «задерживающее, запирающее напряжение» U_з.

На следующих рисунках представлены вольт-амперные характеристики при различных значениях интенсивности (рис.10.9) и частоты (рис10.10), падающего на катод излучении.

Все эти экспериментальные результаты позволили сформулировать следующие законы фотоэффекта:

1.Сила фототока насыщения Is растёт с увеличением освещённости катода (закон Столетова).

2.Запирающая разность потенциалов U_з увеличивается с ростом частоты излучения, падающего на фотокатод.

3.Существует граничная частота - , ниже которой облучение не приводит к возникновению фотоэффекта. Частота называется красной границей фотоэффекта.

4.Фотоэффект безынерциален.

Рис.10.9 Рис.10.10

2.3.Уравнение Эйнштейна для внешнего фотоэффекта.

Ни одна из перечисленных закономерностей фотоэффекта не находит объяснения в рамках классической электродинамики.

Исчерпывающее объяснение это явление получило в теории Эйнштейна.

Эта теория опирается на квантовую природу излучения. Согласно Эйнштейну, излучение не только возникает в виде отдельных порций энергии, чтобы было установлено М.Планком, но и распространяется и поглощается также в виде дискретных порций – гамма-квантов. (Позднее этим сгусткам энергии Комптон дал название фотоны.)

При падении излучения на поверхность проводника, фотоны поглощаются электронами и при этом передают им свою энергию

Закон сохранения энергии, записанный Эйнштейном для фотоэффекта, состоит в утверждении, что энергия фотона, приобретенная электронами, позволяет ему покинуть поверхность проводника, совершив работу выхода. Остаток энергии реализуется в виде кинетической энергии теперь уже свободного электрона

.

«Сразу ясно, - пишет Эйнштейн, - что квантовая теория света дает объяснение фотоэлектрическому эффекту. Пучок фотонов падает на металлическую пластинку. Взаимодействие между излучением и веществом состоит здесь из многих элементарных процессов, в которых фотон ударяется об атом и выбивает из него электрон… Увеличение интенсивности света, на нашем новом языке, означает увеличение числа падающих фотонов. В этом случаи из металлической пластинки будет вырвано большее число электронов...»

Так просто А.Эйнштейн объясняет закон Столетова – первый закон фотоэффекта.

Наличие фототока в цепи при нулевом анодном напряжении тоже можно теперь легко объяснить.

Фотоэлектроны, покинувшие поверхность металла, обладают кинетической энергией. Этой энергии электронам достаточно, чтобы достичь анода и тем самым замкнуть цепь.

Для того чтобы прекратить течение тока в цепи, необходимо на фотоэлемент подать тормозящее запирающее напряжение. Ток исчезнет, когда

.

С увеличением частоты падающего света будет расти энергия фотонов и кинетическая энергия фотоэлектронов

.

Теперь для торможения таких более энергичных электронов потребуется более высокое запирающее напряжение

Такое объяснение получает второй закон фотоэффекта.

Обратимся к третьему закону. Если уменьшать частоту падающего на фотокатод света, будет уменьшаться энергия фотонов и кинетическая энергия фотоэлектронов.

При некотором граничном значении частоты ν_к, кинетическая энергия фотоэлектронов станет равной нулю. Тогда

При дальнейшем снижении частоты, энергия фотонов окажется меньше работы выхода. В результате эмиссия электронов с поверхности металла не состоиться.

Для многих материалов фотокатода эта граничная частота лежит в красной области видимой части спектра. Отсюда и название этой частоты – красная граница фотоэффекта.

И, наконец, - о безынерционности фотоэффекта.

Фотоэлектроны появляются в момент включения освещения катода, так как поглощение фотона электроном происходит за время порядка 1нс = 10^-9 сек.

Заключение.

История рождения квантовой механики свидетельствует о том, что эта новая физическая теория пробивала себе дорогу часто вопреки желанию ученых.

Макс Планк, “выпустивший джина из бутылки”, написав энергию фотона

потом долгие годы пытался спасти классическую электродинамику, всячески ограничивая квантовую природу излучения.

«Будем считать, - говорил он в 1911 году на Сольвеевском конгрессе, - что все явления, происходящие в пустоте, в точности соответствуют уравнениям Максвелла и не имеют никакого отношения к константе h.»

Идею квантования излучения неизменно поддерживал и развивал Эйнштейн:

«Мы должны предположить, что однородный свет состоит из зерен энергии – “световых квантов”, то есть небольших порций энергии, несущихся в пустом пространстве со скоростью света».

Против такого революционного развития квантовой теории света, вновь выступает Макс Планк:

«Мне кажется, что необходимо отказаться от предположения, будто энергия осциллятора обязательно должна быть кратна элементу энергии , и принять, что, наоборот, явление поглощения свободного излучения есть по существу непрерывный процесс…».

Очень многие ученые того времени выражали серьезную озабоченность в связи с рождением квантовой теории.

Анри Пуанкаре:

«До сих пор физика занималась лишь непрерывными величинами, и именно поэтому правомерным было применение дифференциальных уравнений, представляющих основу классической теоретической физики. Не подрывает ли введение квантов правомерность применения дифференциальных уравнений?..».

Зоммерфельд:

«Я думаю, что гипотезу квантов испускания нужно рассматривать как форму объяснения, а не как физическую реальность».

Однако вскоре появились новые неопровержимые экспериментальные доказательства корпускулярной теории излучения.

Одно из них – эффект Комптона – мы обсудим на следующей лекции.

Лекция 11

Экспериментальные основы квантовой теории

(продолжение)

План лекции:

1. Энергия и импульс фотона.

2. Эффект Комптона.

3. Корпускулярно-волновой дуализм.

“…Мы должны предположить, что однородный свет состоит из зерен энергии – световых квантов, т.е. небольших порций энергии, несущихся в пустом пространстве со скоростью света…”

А.Эйнштейн

В самом конце 19 века немецкий физик Макс Планк высказал гипотезу о дискретности теплового излучения. Это был вынужденный революционный шаг ученого, известного своими консервативными взглядами. Только предположив, что тепловое излучение испускается порциями (квантами), ему удалось объяснить все известные к тому времени закономерности теплового излучения абсолютно черного тела. Энергия кванта по Планку пропорциональна частоте излучения ν (ω):

где квант действия, позднее названный постоянной Планка.

Вскоре, анализируя результаты исследования фотоэффекта, А. Эйнштейн приходит к выводу, что излучение не только рождается в виде порций энергии, но поглощается также порциально.

А в 1923 году американский ученый А. Комптон экспериментально доказал, что излучение не только появляется и поглощается порциями, но и распространяется в пространстве как поток частиц – квантов.

Прежде чем приступить к рассмотрению опытов Комптона, определим такие понятия как энергия и импульс фотона и микрочастицы.

1. Энергия и импульс фотона и релятивистской частицы

В релятивистской механике устанавливается связь массы движущейся частицы с ее скоростью.

(11.1)

Это выражение релятивистской массы сегодня не вызывает никаких сомнений, т.к. оно многократно подтверждено экспериментально.

Здесь - «масса покоя» - масса частицы при движении с достаточно малой скоростью. Когда , масса движущейся частицы неотличима от массы покоя .

Энергия релятивистской частицы.

Разложив функцию в биномиальный ряд, получим

Будем считать, что скорость частицы не слишком велика, поэтому можно пренебречь членами высших степеней по сравнению с В этом случае

Здесь – полная энергия движущейся частицы.

– энергия частицы в системе отсчета, относительно которой она покоится (энергия покоя).

Таким образом, полная энергия частицы складывается из ее энергии покоя и кинетической энергии:

(11.2)

Здесь – релятивистская масса частицы.

Теперь установим связь импульса релятивисткой частицы с ее энергией.

Здесь – импульс частицы.

Отсюда следует, что тела, имеющие ненулевую массу покоя , не могут двигаться со скоростью света. И наоборот, частица с нулевой массой покоя движется только со скоростью света.

Такими частицами являются фотоны. Они не существуют в покое ( ), а при движении со скоростью света возникает их релятивистская масса

Действительно, ведь энергия фотона

.

Импульс фотона:

Здесь – волновое число,

– постоянная Планка.

Подведем итог.

Энергия фотона

Импульс фотона

Связь импульса фотона с его энергией

Энергия частицы

Импульс частицы

Связь энергии и импульса релятивистской частицы найдем, объединив два последних выражения.

(11.3)

2. Эффект Комптона.

В истории физики явление, открытое Комптоном, принято считать решающим для победы фотонной теории излучения. В чем оно заключается?

Известно, что при падении излучения на вещество, часть излучения рассеивается, сохраняя неизменную частоту. Такой характер рассеяния легко объясняется классической волновой теорией излучения.

Однако в 1923 году молодой американский физик Артур Комптон обнаружил, что при рассеянии рентгеновских лучей, наряду с классическим явлением рассеяния без изменения частоты, можно наблюдать и рассеяние с уменьшением частоты, то есть с увеличением длины волны . Схема эксперимента Комптона приведена на рис.11.1.

В опыте Комптона изучалось столкновение фотона с «неподвижным» свободным электроном.

Здесь при рассеянии на угол рентгеновских лучей λ обнаруживается излучение с длинной волны

Как свидетельствует эксперимент, разность длин волн рассеянной ( ) и падающей (λ) зависит от угла рассеяния :

Рис.11.1. (11.4)

Здесь λ_с=0,024Å – размерная постоянная эффекта.

Этот результат – еще один пример явления, необъяснимого с точки зрения волновой теории, но понятного, если его рассматривать с позиции квантовой, фотонной теории излучения.

Эффект Комптона легко объясняется, если предположить, что излучение – поток фотонов. При падении на вещество они упруго взаимодействуют с электронами.

Рассмотрим одно такое взаимодействие: фотон – электрон. Для этого абсолютно упругого удара выполняются законы сохранения энергии и импульса системы.

До «столкновения» импульс системы «фотон – электрон» определяется импульсом фотона

Электрон до столкновения будем считать неподвижным.

Энергия системы фотон – электрон перед ударом складывается из энергии фотона и энергии покоя электрона

После взаимодействия изменится импульс фотона ( ) и придет в движение электрон (

При этом энергия системы будет равна сумме новой энергии фотона и электрона:

Здесь мы преобразовали энергию электрона следующим образом:

Теперь запишем законы сохранения:

энергии: (11.5)

импульса: . (11.6)

Первое из этих уравнений (11.5) разделим на скорость света:

(11.7)

Напомним, что волновое число . Возведем уравнение (11.7) в квадрат:

Возведем в квадрат и векторное уравнение закона сохранения импульса (11.6):

Сравнивая два последних выражения, получим:

Домножим обе части этого уравнения на .

И ли

Здесь константа λ_с– комптоновская длина волны электрона.

Теоретический расчет постоянной Комптона дает результат для рассеяния фотонов на свободных электронах Å, великолепно совпадающий с константой, рассчитанной по результатам эксперимента. На рис. 11.3 представлены спектры рассеянного излучения для трех углов рассеяния. Видно, что с увеличением угла рассеяния (45⁰, 90⁰, 135⁰) увеличивается разность длин волн (частот) падающего и рассеянного излучения.

Спектры рассеянного излучения

для трех углов рассеяния.

[Из работы Комптона (1923)]

Рис.11.2

3. Корпускулярно-волновой дуализм излучения.

Особенности теплового излучения абсолютно черного тела, фотоэффект, эффект Комптона – неопровержимо свидетельствуют о корпускулярной природе излучения. Излучение – и свет в том числе – поток порций энергии – фотонов. Фотон обладает энергией и импульсом:

С другой стороны, такие явления как дифракция, интерференция, поляризация убеждают нас в волновой природе излучения. Излучение – электромагнитные волны в широко м диапазоне частот.

С третьей стороны, можно вспомнить о давлении, преломлении света, то есть о явлениях, которые можно объяснить как с позиций классической волновой так и квантовой теории света.

Рассмотрим, например, отражение света от плоского зеркала.

Волновая теория связывает давление света Р с объемной плотностью энергии в электромагнитной волне:

Здесь – поток излучения.

При отражении света, падающие и отраженные волны образуют стоячую волну, плотность энергии в которой

– поток отраженного излучения. Следовательно,

Рис.11.3 давление излучения на отражающее зеркало

Теперь решим эту задачу считая, что свет – поток фотонов (рис.11.4).

При упругом отражении фотона от зеркала, последнее получает импульс

.

Рис.11.4

При падении в единицу времени N фотонов на единичную поверхность зеркала (1м²), давление, создаваемое этим потоком частиц, будет равно суммарному импульсу, переданному ими зеркалу.

.

Здесь – поток энергии падающих фонов .

Нетрудно обнаружить, что в рассмотренной задаче классическая волновая и квантовая корпускулярная теории приводят к совпадающим результатам.

Таким образом, мы приходим к выводу, что излучение (свет) в одних случаях проявляет свои волновые свойства, в других – корпускулярные. В этом и состоит «диалектическое единство противоположностей», нашедшее свое отражение в теории корпускулярно-волнового дуализма излучения.

4. Задача

Фотон рентгеновского излучения с энергией МэВ испытал рассеяние на покоившемся свободном электроне, в результате чего его длина волны увеличилась на =0,015 Å. Найти угол , под которым вылетел комптоновский электрон отдачи.

Решение:

При упругом столкновении фотона со свободным покоящимся электроном выполняется закон сохранения импульса системы (рис.11.5)

Здесь – импульсы фотона до и после взаимодействия,

– импульс электрона отдачи.

Искомый угол  легко связать с углом рссеяния фотона

Рис.11.5 и с соотношением его импульсов .

(11.7)

Воспользовавшись формулой Комптона, вычислим косинус и синус угла :

Импульсы падающего и рассеянного фотонов связаны с их энергиями:

,

Энергия рассеянного фотона:

Теперь можно записать новое выражение импульса фыотона:

.

Подставив в исходное уравнение (11.7) известные теперь значения cosӨ, sinӨ, и , после преобразования получим:

И, следовательно,

Здесь энергия покоя электрона:

Лекция 12

Боровская теория атома водорода.

План лекции

1. Модель атома Томпсона

2. Спектр атома водорода

3. Опыты по рассеянию α-частиц. Планетарная модель атома Резерфорда

4. Постулаты Бора

5. Опыт Франка и Герца

1. Модель атома Томпсона (1903).

К началу 20-ого века было окончательно установлено, что атом – не неделимая частица вещества. Это сложная конструкция, в состав которой входят и заряженные частицы.

В 1900-м году, изучая природу катодных лучей, английский ученый Джозеф Джон Томпсон измерил удельный заряд электрона. Из этих опытов следовало что электроны обладают массой, которая несомненно много меньше массы самого легкого атома – водорода. Было ясно, что электроны являются составными частями всех атомов. Но атомы, как известно, электронейтральны. Это означало, что в атоме присутствуют и положительно заряженные частицы.

Первая электромагнитная не квантовая модель атомы была создана Дж. Дж. Томпсоном. В этой работе он руководствовался следующим постулатом Кельвина о силах притяжения между атомом и электроном: «Притяжение атомом внешнего электрона обратно пропорционально квадрату расстояния между их центрами, а притяжение электрона, находящегося внутри самого атома, пропорционально расстоянию между их центрами».

Такая закономерность характерна для гравитационной силы притяжения тела Землей в предположении, что масса Земли равномерно распределена по объему земного шара. Эта аналогия наводила на мысль о том, что положительный заряд атома равномерно распределен по всему его объему, а электроны атома плавают в этом положительном облаке. В таком случае несложно вычислить силу, действующую на электрон, например, в атоме водорода .

Рис.12.1. Для отыскания напряженности поля Е в той точке атома, где находится электрон, воспользуемся теоремой Остроградского-Гаусса (рис. 12.1):

Здесь - объемная плотность положительного заряда атома.

Таким образом, сила, действующая на электрон в подобном атоме, является квазиупругой и приведет поэтому к колебаниям электрона относительно центра атома.

Частота колебаний электрона:

Это выражение позволяет вычислить радиус атома R считая, что атом излучает электромагнитную волну «реальной» частоты ω₀ ≈ 10¹⁵ с^-1.

Такой расчет дает значение радиуса R ≈ 10^-10 м. Этот результат великолепно совпал с известным к тому времени газокинетическим размером атома.

Но это совпадение стало единственным достижением данной модели. Несостоятельность модель Томпсона проявилась в том, что она не могла объяснить известные к тому времени свойства атомов. Например – закономерности атомных спектров.

2. Спектр атома водорода.

Невзаимодействующие атомы излучают электромагнитные волны определенных, характерных для данного вещества частот. Спектр такого излучения состоит из отдельных линий, которые принято объединять в «серии».

На рисунке 12.2 представлен фрагмент спектра атома водорода (до λ=7000 Ǻ).

Рис.12.2

В 1885 году Иоганн Бальмер показал, что, несмотря на кажущийся беспорядок, в распределении этих спектральных линий существуют закономерности. Он нашел, что частоты линий видимой части спектра атомарного водорода могут быть связаны простой формулой

Ободренные успехом Бальмера, Лаймен, Пашен, Брэкет нашли другие серии в этом излучении.

С ерия Лаймена

С ерия Пашена

Серия Брэккета

Легко видно, что все эти серии описываются похожими формулами, что позволило Бальмеру объединить их в одну.

где и

Это и есть объединенная формула Бальмера. Здесь R=2,07*10¹⁶ с^-1 – постоянная Ридберга

Числа называются спектральными термами атома водорода.

Частота любой линии атома водорода может быть представлена в виде разности соответствующих термов:

Из всех этих эмпирических формул Ритц вывел «комбинационный принцип»:

«Для каждого элемента можно найти совокупность таких чисел – спектральных термов, что частота любой спектральной линии данного элемента равна разности спектральных термов этого элемента.»

Вплоть до 1913 года не было никакого намека на то, каким образом можно было бы теоретически истолковать эти серии, а тем более - комбинационный принцип Ритца. Классическая электромагнитная теория объясняла спектральные линии, но их частоты не имели ничего общего с тем, что давал опыт.

Эмпирические закономерности спектра атома водорода впервые удалось объяснить после создания планетарной модели атома Бора-Резерфорда.

3. Опыт по рассеянию α-частиц. Планетарная модель атома Резерфорда.

Планетарная модель атома родилась в ходе исследования рассеяния α-частиц. Схема этого эксперимента Резерфорда приведена на рис (12.3)

Α льфа-частицы, излучаемые источником А дифрагировались щелью и попадали на экран из сернистого цинка. На экране возникало четкое изображение щели в виде узкой полоски.

Затем между щелью и экраном помещалась тонкая металлическая пластина, вернее, - тонкая золотая фольга Ф. При этом отражение щели на экране размывалось, что и указывало на рассеяние α-частиц веществом пластинки.

Рис.12.3

И менно в этом эксперименте был установлен поразительный факт: очень небольшая часть α-частиц (примерно 1 из 10000!) рассеивалась на значительный угол, отбрасывалась практически назад - к источнику (рис.12.4).

Анализируя этот результат, Резерфорд в 1911 году приходит к следующему выводу: «Рассеяние α-частиц может быть объяснено, если предположить такой атом, который состоит из центрального положительного заряда, сосредоточенного в точке и окруженного однородным сферическим распределением

Рис.12.4 противоположного электричества равной величины».

Позднее статистическая обработка результатов исследования рассеяния α-частиц позволила рассчитать линейный размер ядра атома. Он по оценке Резерфорда составил 10^-15м.

Планетарная модель атома с центральным положительно заряженным ядром и с электронами, вращающимися вокруг него по круговым орбитам, была лишь качественным представлением строения атома.

Резерфорд постулировал движение электронов по круговым орбитам, так как статическая модель атома с неподвижными зарядами оказывалась неустойчивой системой.

Но движущиеся по круговой орбите электроны, должны излучать энергию. Ведь согласно законам классической электродинамики, любой ускоренно движущийся заряд является источником электромагнитных волн. Такое непрерывное излучение энергии должно было очень быстро привести к истощению энергии атома и к падению электрона на ядро.

Выход в этой, казалось бы, безвыходной ситуации удалось найти в 1913 году датскому физику Нильсу Бору.

4. Постулаты Бора (1913).

Для того чтобы обеспечить устойчивость планетарного атома и объяснить особенности атомных спектров, Бору пришлось дополнить классическую электродинамику элементами квантовой теории, которая априори исключает всякую возможность непрерывного излучения.

Свои основные гипотезы Бор формулирует следующим образом:

« 1. Атом может находиться лишь в одном из стационарных состояний. Для таких состояний момент импульса электрона относительно центра его орбиты равен целому кратному постоянной Планка

(12.1)

2. Испускание (или поглощение) энергии происходит не непрерывно, как это принимается в обычной электродинамике, а только при переходе системы из одного «стационарного» состояния в другое.

3. Динамическое равновесие системы в стационарном состоянии определяется обычными законами механики, тогда как для перехода системы между различными стационарными состояниями эти законы не действительны.

4. Излучение, испускаемое при переходе системы из одного стационарного состояния в другое, монохроматично. Соотношение между его частотой ω и общим количеством излученной энергии ∆Е дается равенством

Здесь Е_m и Е_n – энергии атома в двух стационарных состояниях.»

Боровская модель атома водорода.

Модель этого простейшего атома состоит из положительно заряженного ядра (+е) и одного электрона (-е) (рис 12.4).

Пусть электрон движется со скоростью по одной из доступных ему траекторий (r_n). Запишем классическое уравнение движения электрона (II закон Ньютона) и квантовое условие Бора.

Рис.12.4 (12.2)

Отсюда вытекает условие квантования орбит: электрону в атоме водорода доступны круговые орбиты следующих радиусов:

(12.3)

Радиус первой орбиты (n=1) называется боровским радиусом атома . Он составляет

,

что неплохо согласуется с газокинетическим размером атома.

Вычислим внутреннюю энергию атома, которая складывается из кинетической энергии электрона и потенциальной энергии его взаимодействия с ядром. Запишем при этом и уравнение движения электрона (12.2).

Отсюда следует, что энергия атома

(12.4)

В оспользовавшись результатом (12.3) - , получим спектр энергий, доступных атому:

(12.5)

При переходе электрона с «n» орбиты на «m»-ю, атом излучает фотон. Его энергия

(12.6)

Частота этого излучения определяет одну из линий в спектре атома водорода.

(12.7)

С равнивая этот результат с обобщенной формулой Бальмера, приходим к выводу, что

- постоянная Ридберга.

Поразительно численное совпадение этой константы, рассчитанное по Бору, с тем значением, которое было получено в результате анализа спектра излучения атома водорода!

Таким образом, уравнение (12.7) даст все частоты, присутствующие в излучении атома водорода. Это был грандиозный успех планетарной модели атома Резерфорда и Боровской теории этой модели.

Теперь понятно, как возникают спектральные линии и серии в атомарном излучении.

На рисунке 12.5 представлен масштабный чертеж пяти низших Боровских орбит водорода.

П ри движении электрона по одной из этих доступных ему орбит, атом находится в стационарном состоянии и не излучает и не поглощает энергию.

При переходе электрона, например, со второй орбиты (N=2) на первую (N=1) излучается фотон соответствующей частоты. В спектре излучения этот переход отмечен одной из линий в серии Лаймена.

Эта серия включает частоты фотонов, излучаемых при переходе с любой орбиты на первую.

Рис.12.5 Все переходы с орбит n>2 на вторую рождают различные линии серии Бальмера.

И так далее.

Боровская теория наглядно объясняет и комбинационный принцип Ритца.

Обратный переход электрона с одной из нижних орбит на более высокую возможен лишь при поглощении атомом энергии извне.

Прямым экспериментальным подтверждением квантованности электронных орбит в атоме и его энергии явился эксперимент Франка и Герца.

5. Опыт Франка и Герца (1914).

Схема экспериментальной установки, на которой работали Франк и Герц, представлена на рис.12.6.

Рис.12.6 Рис.12.7

В стеклянной колбе, содержащей пары ртути при давлении порядка 1 мм рт.ст., смонтированы анод А, подогреваемый катод К и сетка С.

С помощью потенциометра П можно менять напряжение между катодом и сеткой. Это напряжение является ускоряющим для термоэлектронов, покидающих катод.

Важный момент. Между анодом и сеткой создана тормозящая разность потенциалов порядка 0,5 В, то есть на анод подан отрицательный потенциал относительно сетки.

На рис. 12.7 можно видеть как меняется анодный ток в этой установке при монотонном увеличении ускоряющего напряжения между сеткой и катодом.

Такая необычная зависимость анодного тока от напряжения связана с дискретностью энергетических уровней атомов ртути.

Атом ртути может поглощать порции энергии только вполне определенных величин.

и так далее.

Термоэлектроны, появившиеся на катоде устремляются к сетке. В своем движении они сталкиваются с атомами ртути, но до тех пор, пока кинетическая энергия электронов меньше величины ∆Е₁, эти взаимодействия носят упругий характер. В результате таких соударений электроны практически не теряют энергии. Достигнув сетки, электроны проникают в область между сеткой и анодом и, преодолев тормозящее действие местного поля, достигают анод. Так замыкается цепь и обеспечивается течение анодного тока.

С увеличением ускоряющего напряжения, растет число электронов, достигающих анод, и растет анодный ток. Так продолжается до тех по, пока растущая энергия электронов не достигнет значения ∆Е₁. Теперь взаимодействие электрона с атомом ртути будет носить неупругий характер.

Электрон передаст свою энергию атому ртути, а оставшейся энергии оказывается недостаточно, чтобы преодолеть тормозящее поле между сеткой и анодом. Электрон этим полем отбрасывается назад к сетке. Это первое падение анодного тока, после напряжения U=4.9 В.

При дальнейшем увеличении ускоряющего напряжения упомянутая энергия ∆Е₁ будет достигаться электронами не у самой сетки, а раньше, ближе к катоду. Это означает, что после неупругого взаимодействия с атомом ртути, электрон имеет возможность на оставшемся участке до сетки увеличить свою энергию настолько, чтобы преодолеть тормозящее напряжение.

Вновь можно наблюдать рост тока с увеличением напряжения.

При ускоряющем напряжении больше U>9.8 В, электроны на пути от катода к сетке дважды претерпевают неупругое взаимодействие с атомами ртути. И второе из двух соударений – у самой сетки.

Вновь электроны теряют всю свою энергию на пороге тормозящего поля, и будут отброшены им назад к сетке.

Такая избирательность атомов в отношении к порциям энергии, которые ими могут быть восприняты, является прямым доказательством одного из главных положений квантовой теории - дискретности энергетических уровней атома.

Лекция №13

Волновые свойства микрочастиц

План лекции

1. Волновые свойства вещества. Гипотеза де-Бройля

2. Экспериментальное подтверждение гипотезы де-Бройля

2.1. Опыт Дэвиссона - Джермера

2.2. Волновые свойства микрочастиц. Принцип неопределенности Гейзенберга

3. Уравнение Шредингера

1. Волновые свойства вещества. Гипотеза де-Бройля

Особенности излучения абсолютно черного тела, фотоэффект, эффект Комптона, боровская полуклассическая-полуквантовая теория атома – все это задачи, при решении которых пришлось рассматривать излучение как поток частиц энергии.

Установлены энергия и импульс каждой такой частицы - фотона:

(13.1)

Физика в своем развитии часто встречалась с границами применимости существующих теорий. При этом разрабатывались новые, более общие решения. «Более общие» в том смысле, что старая теория входила в новую как частный, ограниченный случай.

Совсем по-другому сложились взаимоотношения волновой и квантовой оптики. Ни одна из них не стала частью другой. Остались задачи (дифракция…), которые решаются в рамках только волновой теории излучения. Существуют явления (фотоэффект…), которые объясняются только корпускулярной природой света.

Иными словами, как остроумно заметил Уильям Брэгг, сложилась ситуация, когда каждый физик вынужден по понедельникам, средам и пятницам считать свет состоящим из частиц, а в остальные дни - из волны. Лишь при объяснении немногих явлений (прямолинейного распространения света, эффекта Допплера, давления света и др.) можно с равным успехом следовать как одной, так и другой теории.

Такая двойственность теории излучения – корпускулярно-волновой дуализм света – навела молодого французского физика Луи де-Бройля на мысль о глобальном характере этой двойственности.

Если волна – частица, то и материальная частица – волна.

Волна-частица обладает энергией и импульсом (13.1).

По де-Бройлю любая материальная частица обладает волновыми свойствами и может характеризоваться соответствующей частотой и длиной волны

(13.2)

Главный постулат де-Бройля означает, что каждая частица материи является местом и источником связанного с ней колебания. Если эта частица движется, то ее колебание представляется неподвижному наблюдателю в виде волны.

Используя этот подход, де-Броль решил задачу о движении электрона в атоме и пришел к боровским квантовым орбитам (т.е. объяснил происхождение спектров). Эта новая концепция привела де-Бройля к закону Планка для излучения черного тела.

В последующих работах де-Бройль показал, что новые принципы позволяют количественно объяснить эффект Допплера, отражение от движущегося зеркала, давление излучения, приводя к тем формулам, которые дает волновая теория.

Нельзя сказать, что гипотеза де-Бройля о волновых свойствах материи получила восторженный прием в научном мире. В 1925 году Эйнштейн, рекомендуя М.Борну познакомиться с диссертацией Луи де-Бройля, сказал буквально следующее:

«Прочтите ее! Хотя и кажется, что ее написал сумасшедший, но написана она солидно!»

В1926 году эта необычная гипотеза получила свое первое экспериментальное подтверждение.

2. Экспериментальное подтверждение гипотезы де-Бройля

В 1923 году в одном из своих докладов Парижской Академии наук де-Бройль говорил о возможных путях экспериментальной проверки своей теории:

«Поток электронов, проходя через узкую щель, должен был бы дать явление дифракции».

Однако первое подтверждение справедливости волновой механики было получено в опытах по интерференции электронов.

2.1. Опыт Дэвиссона –Джермера (1926)

На рис. 13.1 представлена схема этого опыта.

Здесь пучок ускоренных электронов направлялся на монокристалл никеля. Одна из вершин этого кристалла сошлифована перпендикулярно к большой диагонали кристаллической ячейки.

Отраженные электроны улавливались «цилиндром Фарадея», соединенным с гальванометром. Этот измерительный цилиндр мог перемещаться по дуге вокруг кристалла. Сам кристалл тоже мог поворачиваться относительно оси, совпадающей с направлением падающего пучка электронов.

Расстояние между атомными плоскостями монокристалла никеля – d было известно из рентгенографических исследований.

Как следует из графиков рис.13.2, сила тока рассеянных электронов оказалась максимальной при определенном значении угла рассеяния θ.

Рис.13.1

Рис.13.2

Длина волны, соответствующая этому интерференционному максимуму, оказалась равной (см. рис.13.3):

, Å.

. В то же время легко рассчитать длину волны

де-Бройля падающих электронов

=1.67Å.

Здесь - скорость электронов при

у скоряющем напряжении

Совпадение этих длин волн и явилось первым подтверждением волновых свойств частиц – в данном случае электронов.

Вскоре удалось наблюдать экспериментально и дифракцию электронов.

Это явление исследовалось в лабораториях П.С. Тартаковского, Г.П. Томсона, В.А.Фабриканта и др. ученых.

Схемы их опытов очень близки (рис. 13.3)

Рис.13.3 Рис.13.4

Тонких пучок ускоренных электронов пронизывал золотую фольгу (в опытах П.С. Тартаковского) и падал на фотопластинку.

Результат дифракции электронов на кристаллической решетке приведен на рис. 13.4.

2.2. Волновые свойства микрочастиц. Принцип неопределенности Гейзенберга

На рис. 13.5 приведена схема мысленного эксперимента, поясняющего необычные свойства микрочастиц.

Рис.13.5

Здесь пучок ускоренных электронов падает на экран с двумя узкими щелями. Если закрыть одну щель, то электроны, прошедшие через другую, рассеются так, как показано на рис. 13.6а.

П одобное же распределение, но несколько смещенное будет получено, если закрыть вторую щель и открыть первую (рис. 13.6б)

Теперь оставим открытыми обе щели. Здравый смысл подсказывает, что новое распределение частиц должно равняться сумме первых двух (рис.13.6в)

Однако опыт свидетельствует совсем о другом (рис.13.7)

Распределение электронов отвечает интерференции двух когерентных волн!

Таким образом, на движение каждого отдельного электрона оказывают влияние обе щели!

Рисс.13.6

Рис.13.7

Этот мысленный эксперимент подтверждает тот факт, что микрочастица-волна не просто «маленькое» материальное тело. Это объект, наделенный особыми свойствами, присущими элементам микромира.

Так, например, нельзя указать траекторию микрочастицы, измерить одновременно ее скорость и координату…

Рассмотрим еще один пример: дифракцию микрочастиц на щели.

Поток микрочастиц подлетает к экрану со щелью (рис.13.8). Пусть экран перпендикулярен потоку.

Рис.13.8

Достоверно известно, что перед щелью х-компонента импульса микрочастицы Здесь скорость частиц перпендикулярна экрану, т.е. оси x. Погрешность это сведения

Но при этом совершенно не определена х-координата частицы.

Теперь рассмотрим движение частицы-волны в щели ∆х.

За щелью дифрагировавшие частицы будут отклонены в пределах угла ±φ.

Э то максимальный угол, соответствующий дифракционному минимуму

О тклонение на угол φ означает, что у микрочастицы появилась х-компонента импульса

К роме того, теперь в щели мы можем указать х-координату с погрешностью

Тогда или

Последний результат обобщен Гейзенбергом и сформулирован как один из основных принципов квантовой механики.

Принцип неопределенностей Гейзенберга:

П роизведение неопределенностей значений двух сопряженных переменных не может быть меньше

(13.3)

Сопряженными величинами являются координаты и соответствующие проекции импульса, энергия и время. Произведение неопределенностей этих величин не может быть меньше по порядку величины постоянной Планка т.е.

(13.4)

Последнее соотношение означает, что чем точнее мы хотели бы померить энергию частицы, тем большее время займет это измерение.

3. Уравнение Шредингера

В 1926 году швейцарский физик Эрвин Шредингер записал в явном виде уравнение для волн волновой механики.

И сегодня до конца не ясно, как он нашел это уравнение.

Может быть, он рассуждал следующим образом.

Согласно гипотезе де-Бройля, каждой движущейся микрочастице должна быть сопоставлена волна.

Пусть свободной микрочастице, летящей вдоль оси x, соответствует плоская волна

(13.5)

Свяжем параметры волны с энергией и импульсом микрочастицы

Теперь уравнение (13.5) можно записать иначе:

(13.6)

Продифференцируем это выражение один раз по времени и дважды – по координате:

(13.7)

(13.8)

В случае свободного движения нерелятивистской частицы, ее энергия и импульс

связаны простым соотношением:

Теперь, принимая во внимание это соотношение, легко связать уравнения (13.7) и (13.8)

(13.9)

Это и есть волновое уравнение Шредингера для одномерного движения свободной частицы.

В случае движения микрочастицы в силовом поле, потенциальная энергия U, полная энергия E и импульс частицы связаны таким соотношением

Объединяя в этом выражении уравнения (13.7) и (13.8), получим:

Или еще так

(13.10)

Это уравнение Шредингера для одномерного движения микрочастицы в силовом поле.

Д ля частицы, движущейся в произвольном направлении, запишем волновое уравнение в таком виде:

(13.11)

Это уравнение получило название нестационарное волновое уравнение Шредингера.

Здесь оператор Лапласа. Таким образом

При движении микрочастицы в стационарном (неизменном во времени) силовом поле, решение уравнения Шредингера может быть представлено произведением двух множителей, один из которых является функцией только координат, а другой – только времени

(13.12)

Используем это решение в дифференциальном уравнении (13.10)

(13.13)

Сократив на общий множитель , получим уравнение Шредингера для стационарных состояний:

(13.14)

Это же уравнение можно представить еще и в таком виде:

Итог.

Уравнения Шредингера

1) Для одномерного движения свободной частицы (U=0)

2) Для одномерного движения частицы в силовом поле

3) Нестационарное волновое уравнение

4 ) Стационарное волновое уравнение

Мы познакомились с различными уравнениями движения микрочастиц – с волновыми уравнениями Шредингера. Но до сих пор остается не ясным: каково содержание самой Ψ – функции?

Рассматривая, например, акустическую волну, мы составляли волновое уравнение для давления или плотности среды. В волновом уравнении электромагнитной волны речь шла о напряженности электрического или магнитного полей…

Что же означает в уравнении Шредингера пси-функция (Ψ)? Каков ее физический смысл?

Этот вопрос мы подробно обсудим на следующей лекции.

Лекция 14. <<Уравнение Шредингера>>.

План лекции:

1. Уравнение Шредингера. Волновая функция и её физический смысл.

2. «Квантование как проблема собственных значений».

   1. Частица в бесконечно глубокой одномерной потенциальной яме.

   2. Туннельный эффект.

1. Уравнение Шредингера. Волновая функция и её физический смысл.

В самом начале 1923 года молодой французский физик Луи де Бройль опубликовал свою теорию волновой природы вещества. Основные положения теории были изложены в трёх его знаменитых докладах, предоставленных им Парижской Академии наук. Ключевым постулатом теории являлось предположение, что с каждой частицей с массой покоя связан волновой процесс с частотой .

При этом

.

Здесь - постоянная Планка, - скорость света в пустоте.

Вскоре новая волновая механика получила неопровержимые экспериментальные подтверждения в работах Дависсона, Джермера, Томсона, Тартаковского, Фабриканта, и других исследователей.

Идея де Бройля привлекла внимание швейцарского физика Эрвина Шредингера. В 1926 году ему удалось в явном виде записать уравнение для волн волновой механики, т.е. для дебройлевских волн, связанных с материальными частицами

(14.1)

Важным отличием этого волнового уравнения от классических уравнений распространения различных волн состоит в присутствии мнимых коэффициентов в уравнении Шредингера. Эти мнимые коэффициенты принципиально неустранимы и в волновой - функции.

Тем самым математически подтверждается тот факт, что волнам де Бройля, сопряженным с частицами, нельзя приписать “физического существования”. Поэтому сам де Бройль называл эту волну «фиктивной», а Эйнштейн окрестил её «волной-призраком».

Но вскоре за этими волнами закрепилось другое название: «волны вероятности».

В 1927 годы Гейзенберг и Борн пришли к выводу, что квадрат модуля волновой функции в любой точке пространства и в любой момент времени есть мера того, что соответствующая частица находится в этой точке и в этот момент. Иными словами Борн и Гейзенберг предполагают существование частицы и связанной с ней непрерывной волны , но частица не имеет ни определённой скорости, ни определённой траектории. Речь может идти лишь о вероятности нахождения частицы в той или иной области пространства. Эту вероятность и определяет волна ψ – функции - решение уравнения Шредингера.

Таким образом, вероятность dP обнаружить частицу в объёме можно записать в следующем виде

(14.2)

Здесь - коэффициент пропорциональности.

Так как вероятность обнаружить частицу в пространстве равна единице («достоверное событие»), то

Обычно выбирают - функцию так, чтобы , т.е.

Этот интеграл представляет собой «условие нормировки».

Волновая функция ( ), удовлетворяющая условию нормировки, называется нормированной функцией. Для нормированной -функции

(14.3)

В случае стационарного силового поля

Это означает, что плотность вероятности обнаружить частицу в заданной точке стационарного поля, не меняется со временем:

(14.4)

Ещё раз отметим, что в волновой механике нет таких понятий классической механики как траектория, «точное» положение или «точная» скорость микрочастицы.

-функция позволяет предсказать лишь вероятность обнаружения частицы в различных точках пространства.

На следующих двух примерах поясним, как решаются конкретные задачи о движение микрочастиц с помощью волнового уравнения Шредингера.

2. «Квантование как проблема собственных значений».

Именно такое название носит знаменитая работа Шредингера по волновой механике. Смысл этого названия состоит в следующем.

Так как - функция связана с вероятностными характеристиками, эта функция должна быть однозначной, непрерывной, конечной и, кроме того, она должна иметь непрерывную и постоянную производную. Эти требования к - функции получили название «стандартные условия».

Доказано, что уравнение Шредингера имеет решения, удовлетворяющие стандартным условиям, не при любых значениях полной энергии частицы . Эти значения энергии образуют ряд так называемых собственных значений .

-функции, соответствующие этим собственным значениям энергии, называются собственными функциями.

Покажем, что волновое уравнение Шредингера автоматически приводит к дискретности энергии частицы и к энергетическим уровням.

1. Частица в бесконечно глубокой одномерной потенциальной яме.

Рассмотрим, какие энергии доступны частице, помещённой в ящик длиной с бесконечно высокими стенками (рис 14.1). Здесь частице позволено двигаться вдоль оси на участке от до . Потенциальная энергия частицы внутри ящика равна при и бесконечна за пределами потенциальной ямы когда и . Воспользуемся стационарным уравнением Шредингера:

(14.5)

Так как частица не может оказаться за пределами ямы (вероятность такого события равна 0), то -функция вне ямы и на её границе равна нулю:

Д ля частицы внутри потенциальной ямы, где U=0, волновое уравнение принимает следующий вид:

(14.6)

Подобное дифференциальное уравнение хорошо известно из теории колебаний. Его решение

где

Выясним значение констант и , воспользовавшись граничными условиями. При x=0

Это означает, что .

Рис. 14.1.

Воспользуемся вторым граничным условием: при x=l

Отсюда следует, что . Вспомнив, что , получим набор собственных значений энергии:

. (14.7)

Так уравнение Шредингера ненасильственно приводит к дискретности энергии частицы в потенциальном ящике. Внутри потенциальной ямы частице доступны лишь вполне определённые значения энергии (рис.14.2).

Рис.14.2

О тыщем теперь собственные значения волновой функции

Здесь осталось определить только амплитуду, для чего воспользуемся условием нормировки:

поэтому

Теперь собственные функции можно представить так

(14.8)

Рис14.3

Графики собственных функций и плотности вероятности приведены на рис.14.3. Попробуйте проанализировать полученные результаты.

Например, при вероятность обнаружить частицу в центре ямы равна нулю, а при эта вероятность максимальна !