6.2. Оценка разности

Оценка разности применяется тогда, когда аудитор считает, что в отчете по самооценке (анализируемой генеральной совокупности) содержатся ошибочные данные (как правило, завышенные), диапазон расхождения которых необходимо оценить на основе выборочных данных. Для этого выполняются следующие процедуры.

1. Определяется необходимый объем выборки.

2. Вычисляются разности R_i между значениями, реально полученными в ходе аудита, и значениями, представленными в отчете самооценки. При этом:

R_i = 0, если данные внутреннего и внешнего аудитов совпадают;

R_i > 0, если данные внутреннего превышают соответствующие значения внешнего аудита;

R_i < 0, если данные внутреннего меньше соответствующих значений внешнего аудита.

3. Вычисляется средняя выборочная разность , которая является результатом деления суммы разностей на объем выборки:

.

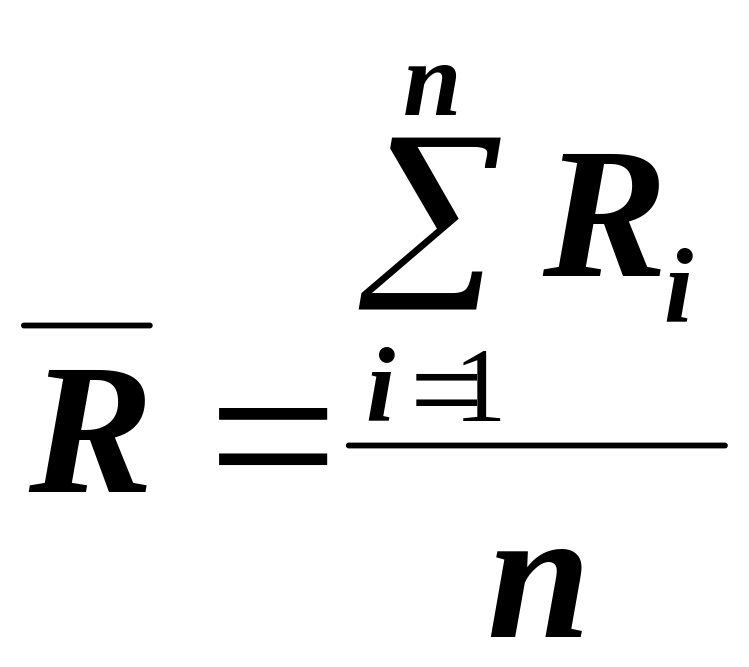4. Вычисляется стандартное отклонение разностей S_R. Элементам выборки, не являющимся ошибками, соответствуют нулевые разности.

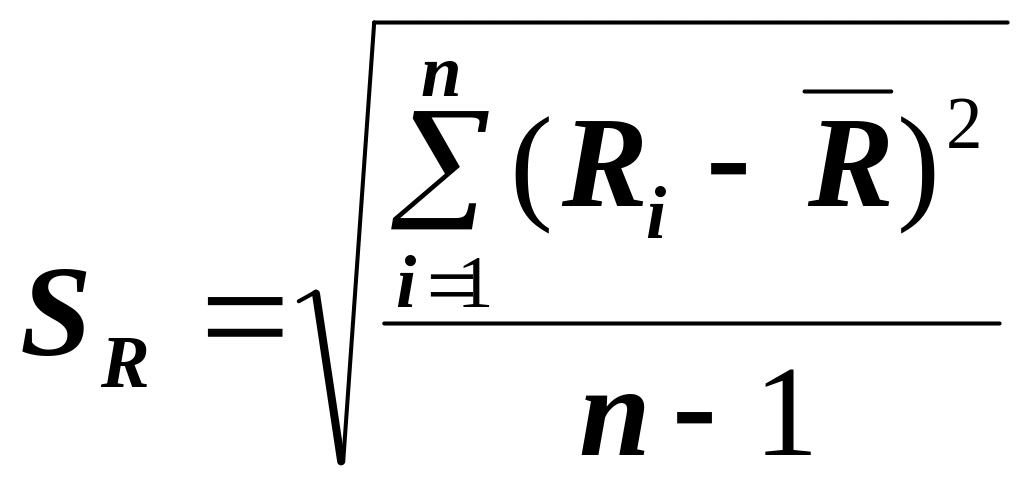
5. Вычисляются границы доверительного интервала ∆SR_i, содержащего сумму разностей элементов генеральной совокупности:

(15)

Выражение (15) может быть также использовано для оценки качества работы подразделений организации, деятельность которых сопряжена с обработкой большего объема цифровой информации.

Пример 3. Продемонстрируем применение формулы (15) для проверки качества работы бухгалтерии вуза. Предположим, что по результатам проверки бухгалтерии необходимо построить 95%-й доверительный интервал, содержащий полную разность между фактическими суммами, указанными в накладных, и суммами, занесенными в информационную систему. В выборку, состоящую из 100 записей, входят 12 накладных, не соответствующих действительности. Перечислим эти разности, выраженные в рублях.

9,3

7,47

17,32

8,30

5,21

10,80

6,22

5,63

4,97

7,43

2,99

4,63

В остальных 88 накладных ошибок нет, следовательно, их разности равны нулю.

Решение.

Средняя выборочная разность и стандартное отклонение разностей S_R соответственно равны:

;

.

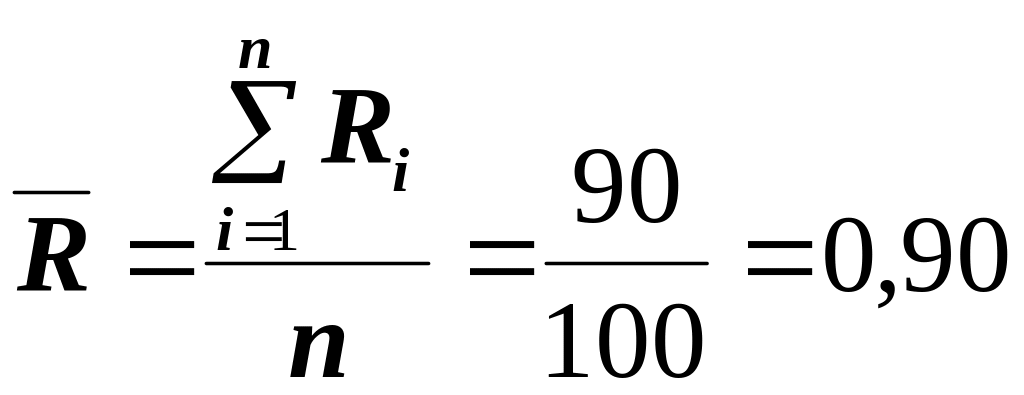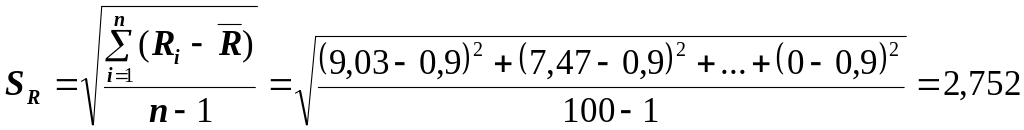Границы доверительного интервала, содержащего полную разность для всей генеральной совокупности, состоящей из 5000 накладных, вычисляют по формуле (15):

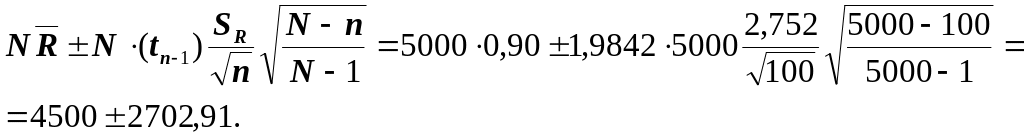
1797,09 ≤ ∆SR_i ≤ 7202,91.

Следовательно, вероятность того, что полная разность генеральной совокупности накладных не меньше 1 797,09 и не больше 7 202,91, равна 0,95.

В рассмотренном ранее примере все 12 разностей были положительными. Разумеется, ошибки могут быть не только положительными, но и отрицательными. Проиллюстрируем это с помощью следующего примера.

Пример 4. Предположим, что в выборке, состоящей из 100 записей, обнаружены 14 ошибочных записей. Перечислим их разности, выраженные в рублях.

75,41	38,97	108,54	-37,18	62,75	118,32	-88,84
127,74	55,42	39,03	29,41	47,99	28,73	84,05

Необходимо построить 95%-й доверительный интервал, содержащий полную разность генеральной совокупности, состоящей из 1 000 накладных.

Решение.

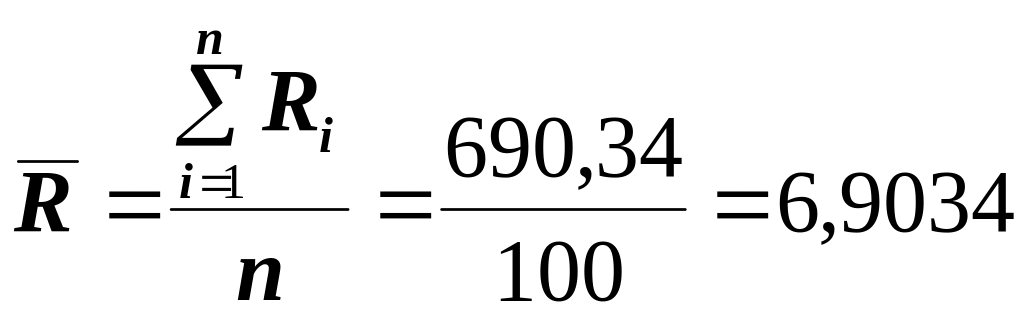
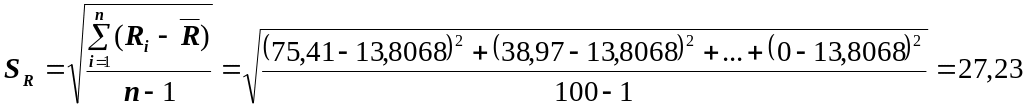
Границы 95%-го доверительного интервала, содержащего полную разность, определяем по формуле (15):

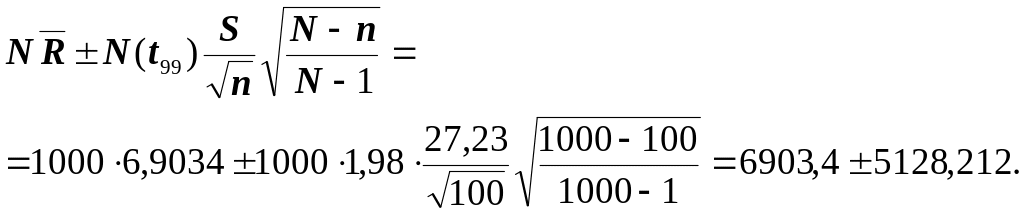
1775,19 < ∆SR_i < 12031,61.

Следовательно, вероятность того, что полная разность генеральной совокупности не меньше 1775,19 и не больше 12031,61, равна 0,95.

N	n		Ri	1-a	t	1/2	min (∆SRi)	max (∆SRi)	∆SRi	SR
1000	50	0,4	20	95	2,09	573,73	- 173,73	973,73	400
100	50	0,4	20	95	2,09	41,81	-1,81	81,81	40
100	50	0	0	95	2,09	32,897	-32,90	32,90	0
100	50	0	0	95	2,09	50,31	-50,31	50,31	0
100	50	0	0	99	2,68	67,09	-67,09	67,09	0
100	50	0	0	90	1,68	41,97	-41,97	41,97	0
100	20	3,3	66	95	2,09	163,85	166,15	493,85	330	3,89
100	20	3,3	66	99	2,86	223,97	106,03	553,97	330	3,89
100	20	3,3	66	90	1,73	135,37	194,63	465,37	330	3,89
1000	20	3,3	66	90	1,73	1491,5	1808,5	4791,5	3300	3,89

2	2	2	4	4	4	1	1	1	1
-3	-3	-2	-4	-4	-4	2	2	2	2
4	4	4	4	4	4	3	3	3	3
5	5	-2	-2	-2	-2	4	4	4	4
2	2	-2	-2	-2	-2	5	5	5	5
6	6	-6	-6	-6	-6	6	6	6	6
-7	-7	2	2	2	2	7	7	7	7
-3	-3	2	2	2	2	8	8	8	8
4	4	2	2	2	2	9	9	9	9
5	5	-5	-10	-10	-10	10	10	10	10
5	5	5	10	10	10	11	11	11	11