VI. Применение доверительных интервалов при проведении самооценки смк

Описывая доверительные интервалы, мы сосредоточили внимание на математическом ожидании и доле признака в генеральной совокупности. Эти средства статистического анализа могут быть использованы при проведении анализа результатов самооценки эффективности функционирования систем менеджмента качества.

В настоящее время основной тенденцией в области гарантий качества становится перенос центра тяжести с процедур внешнего контроля качества деятельности организации в сторону внутренней самооценки (самообследования) на основе тех или иных моделей управления качеством. Эффективная система мониторинга качества, основанная на самооценке, сама по себе обеспечивает объективную оценку и доверие к деятельности организации и приводит к существенной экономии материальных и временных ресурсов, выделяемых на проведение внешней экспертизы. Результаты самооценки становятся с одной стороны механизмом постоянного внутреннего улучшения системы качества, а с другой – могут представляться внешним проверяющим для их выборочной проверки.

Самооценка может использоваться для сравнения своей деятельности с лучшими в определенном классе достижениями других организаций или показателями мирового уровня в данной области (технология бенчмаркинга), а также может быть полезной при сравнении с поставленными ранее целями при повторных оценках степени достижения этих целей.

Эффективность и качество самооценки могут быть оценить степенью согласованности ее результатов с результатами выборочной проверки.

6.1. Оценка суммы элементов генеральной совокупности

По результатам самооценки комиссия, проводившая внутренний аудит, формирует итоговый отчет, в котором приводится суммарный результат (СМК) в виде суммы баллов , характеризующих систему менеджмента качества по всем сторонам деятельности (N критериям), предусмотренным для той или иной СМК. В процессе выборочной проверки, прежде всего, предстоит оценивать эту сумму баллов , набранных для генеральной совокупности. Точечная оценка суммы элементов генеральной совокупности S равна объему критериев генеральной совокупности N, умноженному на выборочное среднее , полученному в результате внешнего аудита по n критериям СМК:

S = . (13)

Границы доверительного интервала ∆S, содержащего сумму элементов генеральной совокупности, определяются по формуле (14):

(14)

Пример 1. Чтобы продемонстрировать применение формулы (14), предположим, что СМК организации оценивается по 100 критериям качества (N =100). В ходе внешнего аудита проверено 30 критериев (n = 30) и из анализа данных выборки получены следующие результаты: =55,7, S = 18,5.

Необходимо построить 95% доверительный интервал, содержащий сумму баллов, которую организация может получить при ее оценке по всем 100 критериям.

Решение.

Из табл. 2 имеем, t₂₉ = 2,045.

S = 100  55,7 = 5570.

Границы доверительного интервала равны:

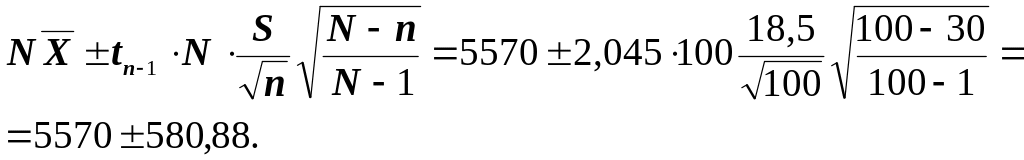
Откуда: 4989,12 ≤ ∆S ≤ 6150,88.

Следовательно, с вероятностью 0,95 можно утверждать, что сумма баллов, которую может получить организация при оценке СМК по 100 критериям не меньше 4989,12 и не больше 6150,88. Если этот интервал не накрывает итоговый результат, представленный в отчете по самооценке, то необходимо провести дополнительные исследования и анализ данных внутреннего аудита.

N	n		S	1-	t	S	1/2(∆S)	min((∆S))	max(∆S)
100	30	55,7	18,5	0,95	2,05	5570	580,88	4989,12	6150,85
1000	100	1076,39	273,62	0,95	1,98	1076390	51531,82	1024858,18	1127921,82
100	20	2,39	12,62	0,95	2,09	239	530,94	- 291,94	769,94
100	20	2,39	2,62	0,95	2,09	239	110,23	128,77	349,23
500	20	2,39	2,62	0,95	2,09	1195	601,31	593,69	1796,31
500	20	2,39	2,62	0,99	2,86	1195	821,93	373,07	2016,93
500	20	2,39	2,62	0,9	1,73	1195	496,77	698,23	1691,77
500	40	2,39	2,62	0,9	1,68	1195	335,07	859,93	1530,07
500	40	2,39	2,62	0,95	2,02	1195	402,25	792,75	1597,25
500	40	2,39	2,62	0,99	2,71	1195	538,52	656,48	1733,52
65	5	27,27	8,95	0,95	2,78	1772,55	699,40	1073,15	2471,95
65	5	17,27	8,95	0,95	2,78	1122,55	699,40	423,15	1821,95

Пример 2. Менеджер по качеству базы хранения овощной продукции желает оценить условия хранения картофеля. На склад хранения было заложено 1000 мешков качественного картофеля (N =1000). Через 1 год хранения проверке на его сохранность подвергается 100 мешков (n =100), По выборке вычисляются среднее значение испорченного картофеля и стандартное отклонение. В результате получено:

выборочное среднее = 2,39 кг;

стандартное отклонение S = 2,62 кг.

Необходимо построить 95%-ный доверительный интервал, содержащий общее количество испорченного картофеля, хранимого на складе.

Решение.

Используя формулу (13), получим точечную оценку общего количества испорченного картофеля S, хранимого в течение года на складе:

S = N = 1 000  2,39 = 2390.

Далее, по формуле (14) вычисляем границы 95%-го доверительного интервала для S.

1896,57 ≤ ∆S ≤ 2883,43.

Следовательно, с вероятностью 0,95 можно утверждать, что за год хранения картофеля на складе, количество испорченного картофеля, будет находиться в диапазоне от 1896,57 кг до 2883,43 кг.