V. Определение объема выборки

В каждом из рассмотренных выше примеров мы заранее фиксировали объем выборки, не учитывая ширину доверительного интервала. В реальных задачах оценки качества и управления качеством важно установить объем выборки по возможности малым, но таким, чтобы оценка соответствовала требованиям точности (см. рис.3). Это зависит от наличия финансовых ресурсов, времени и легкости создания выборки. Иначе говоря, следует задать ошибку выборочного исследования, допускаемую при оценке каждой из анализируемых характеристик. Кроме того, необходимо заранее определить доверительный уровень оценки истинного параметра генеральной совокупности.

5.1. Определение объема выборки для оценки математического ожидания

Чтобы определить объем выборки, необходимый для оценки математического ожидания генеральной совокупности, следует учесть величину ошибки выборочного исследования и доверительный уровень. Еще необходима дополнительная информация о величине среднего квадратического отклонения.

Для того чтобы вывести формулу, позволяющую вычислить объем выборки, вспомним формулу:

,

где Z — критическое значение случайной величины, имеющей стандартизированное нормальное распределение.

Величина, добавляемая и вычитаемая из , равна половине длины доверительного интервала. Она определяет меру неточности оценки, возникающей вследствие ошибки выборочного исследования, которая обозначается символом ε и вычисляется по формуле

(9)

Следовательно, объем выборки п определяется по формуле:

(10)

Таким образом, для определения объема выборки необходимо знать три параметра:

• величину Z, являющуюся критическим значением стандартизованного нормального распределения⁶

• приемлемую ошибку выборочного исследования ε;

• средне квадратическое отклонение σ.

n = 1

n = 2

n = 32

n = 4

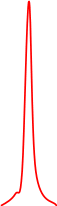
Х

Рис. 3. Выборочные распределения средних арифметических, построенные по 500 выборкам с объемами п = 1; 2; 4 и 32, извлеченным из нормально распределенной генеральной совокупности

На практике вычислить эти величины непросто. Как определить доверительный уровень и ошибку выборочного исследования? Обычно ответить на этот вопрос могут лишь эксперты в предметной области (т.е. люди, понимающие смысл оцениваемых величин). Как правило, доверительный уровень равен 95% (в этом случае Z= 1,96). Если требуется поднять доверительный уровень, обычно выбирают величину, равную 99%. Если можно ограничиться более низким доверительным уровнем, выбирают 90%. Определяя ошибку выборочного исследования, не стоит думать о ее величине (в принципе, любая ошибка нежелательна). Следует задать такую ошибку, чтобы полученные результаты допускали разумную интерпретацию.

Кроме доверительного уровня и ошибки выборочного исследования, необходимо знать стандартное отклонение генеральной совокупности. К сожалению, этот параметр для потребителя почти никогда не известен. В некоторых случаях стандартное отклонение генеральной совокупности можно оценить на основе результатов предшествующей эксплуатации. В других ситуациях опытный менеджер по качеству может учесть размах выборки и распределение случайной переменной. Например, если генеральная совокупность имеет нормальное распределение, ее размах приближенно равен 6σ (т.е. ±3σ в окрестности математического ожидания). Следовательно, стандартное отклонение приближенно равно одной шестой части, диапазона. Если величину σ невозможно оценить таким способом, необходимо спланировать и выполнить экспериментальные проверки.

Чтобы продемонстрировать применение этого подхода, рассмотрим простейший пример.

Пример 1. С помощью выборочного метода необходимо оценить средний стаж работы служа­щих крупной фирмы. Предполагается, что он подчиняется нормальному закону, и по результатам предыдущих исследований аналогичных организаций известно, что стан­дартное отклонение σ равно 2,70 года. Необходимо установить объем выборки с 95%-м доверительным уровнем и погрешностью, не превышающей величины 0,5 года.

Решение. По формуле (10) получаем:

Следовательно, п = 113, поскольку дробные результаты, как правило, округляют с избытком до ближайшего целого.

Ответ. Чтобы с вероятностью 0,95 и ε= 0,5 года определить средний стаж работы служа­щих крупной фирмы, необ­ходимо обследовать не менее 113 служащих.

Для этого же примера при 95% -м доверительном уровне определите, как изменится объем выборки при следующих условиях:

σ=2,7; ε= 0,1; п = 2801 ?

σ=2,7; ε= 1; п = 29 ?

σ=5; ε= 0,5; п = 385 ?

σ=1; ε= 0,5; п = 16 ?

Проверьте правильность приведенных ответов и поясните полученные результаты.

Для этих же условий найдите решения для 90%-го доверительного уровня.