2.4. Формули в алгебрі логіки

Використовуючи елементарні логічні функції, можна побудувати будь-яку формулу.

Нехай , тобто Р — підмножина множини всіх логічних функцій .

Визначення 2.5. Функцію називають формулою над . Якщо і є або формулами над , або символами змінних, то вираз також називають формулою над P.

Формули називають еквівалентними, якщо функції, які вони реалізують, рівні.

Приклад 2.4. Формули , , , , , , , , , , є еквівалентними, оскільки вони задають ту саму функцію . Це легко перевірити, побудувавши відповідні таблиці істинності. Зауважимо, що, крім поданих, ще можна вказати багато інших формул, які задають цю функцію.

2.5. Диз’юнктивні й кон’юктивні нормальні форми алгебри Буля

Визначення 2.6. Кон’юктивним одночленом (елементарною кон’юнк­цією) від змінних називають кон’юнкцію цих змінних або їхніх заперечень.

Визначення 2.7. Диз’юнктивним одночленом (елементарною диз’юнк­цією) від змінних називають диз’юнкцію цих змінних або їхніх заперечень.

При цьому в одночлен не обов’язково мають входити всі змінні.

Приклад 2.5. Якщо дано три змінні х, y і z, то , , , , тощо є кон’юктивними одночленами від цих змінних, а , , , , , тощо є диз’юктивними одночленами.

Визначення 2.8. Диз’юнкцію кон’юнктивних одночленів називають диз’юнктивною нормальною формою (ДНФ).

Визначення 2.9. Кон’юнкцію диз’юнктивних одночленів називають кон’юнктивною нормальною формою (КНФ).

Приклад 2.6. Для функції її диз’юнктивними нормальними формами (ДНФ) є формули і , а кон’юнктивними нормальними формами (КНФ) — формули і .

Для кожної функції алгебри логіки існують множини ДНФ і КНФ.

Щоб логічну функцію, задану формулою, подати за допомогою ДНФ чи КНФ, треба спочатку в формулі всі операції виразити через диз’юнкцію, кон’юнкцію і заперечення:

; ;

; ;

; ,

а потім, використовуючи закони де Моргана, одержати формулу, в якій заперечення стоятимуть лише над окремими змінними, і застосувати відповідний дистрибутивний закон.

Приклад 2.7. Одержимо ДНФ функції . Для цього виразимо імплікацію і стрілку Пірса через подані вище тотожності і виконаємо еквівалентні перетворення, враховуючи властивості логічних функцій:

.

Приклад 2.8. Одержимо КНФ функції . Для цього звільнимося від імплікації і проведемо перетворення:

.

Використовуючи закони дистрибутивності й поглинання, можна суттєво спростити одержану КНФ:

Отже, . А це одночасно ДНФ і КНФ.

2.6. Двоїсті функції

В алгебрі логіки досить важливим є поняття двоїстої функції.

Визначення 2.10. Логічну функцію називають двоїстою до логічної функції , якщо виконується рівність: .

Очевидно, що .

Із визначення двоїстої функції випливає, що для побудови її таблиці істинності треба інвертувати (тобто замінити 0 на 1, а 1 на 0) стовпчик значень функції і перевернути його.

Приклад 2.9. Побудуємо таблицю істинності функції, двоїстої до функції :

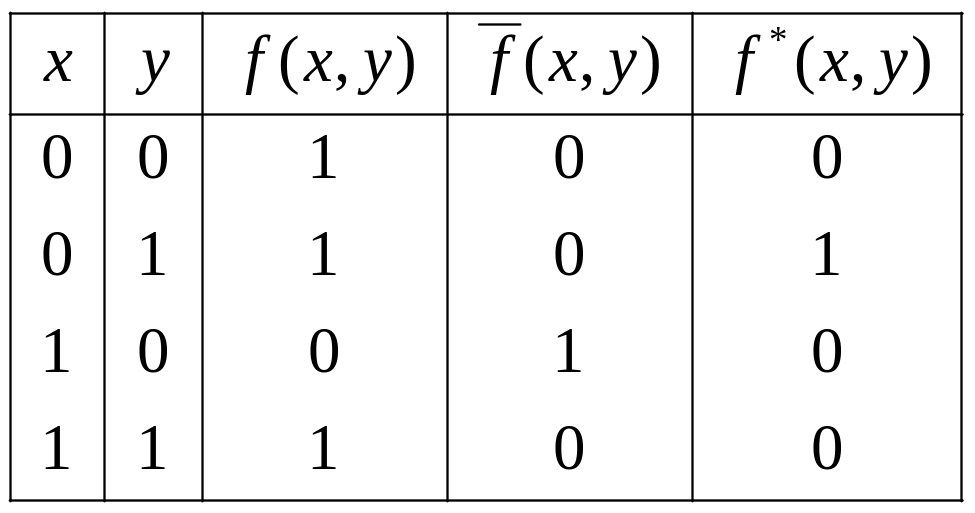
Для формул алгебри логіки справедливий принцип двоїстості: якщо формула реалізує логічну функцію , то формулу називають двоїстою до і вона реалізує функцію .

Приклад 2.10. Знайдемо пари двоїстих функцій серед елементарних. Якщо , то за визначенням двоїстої функції ; якщо , то ; якщо , то . Якщо , то за визначенням двоїстої функції . Трохи важче знайти двоїсту функцію до функції еквівалентності: відповідно до визначення функції еквівалентності вектором її значень є вектор ; побудуємо вектор двоїстої функції — візьмемо інверсію і запишемо елементи вектора в зворотному порядку — ; одержаний вектор значень відповідає функції додавання за модулем два . Аналогічно можна знайти двоїсті функції для інших елементарних логічних функцій.

Отже, серед елементарних двоїстими функціями є такі:

0 і 1; х і х; і ;

і ; і ; і ;

і ; і .

При побудові двоїстої формули часом, щоб зберегти порядок виконання операцій, треба використовувати дужки.

Приклад 2.11. Відповідно до принципу двоїстості двоїстою для логічної функції є функція .

В алгебрі Буля принцип двоїстості формулюється так: для одержання двоїстої формули , треба у формулі виконати взаємні заміни 0 на 1, 1 на 0, символа кон’юнкції ( ) на символ диз’юнкцію ( ) і навпаки.

Приклад 2.12. Відповідно до принципу двоїстості в алгебрі Буля, двоїстими є такі формули: і ; і . Двоїстими також є тотожності: і ; і ; і ; і ; , тощо.

Визначення 2.11. Логічну функцію називають самодвоїстою, якщо вона дорівнює своїй двоїстій функції , тобто виконується рівність .

Серед функцій однієї і двох змінних самодвоїстими є функції: і . Усіх самодвоїстих функцій від змінних є .

Приклад 2.13. Визначимо, чи є самодвоїстою логічна функція . Відповідно до принципу двоїстості двоїста функція має вигляд: . Щоб перевірити, чи рівні ці дві функції, виконаємо перетворення:

.

Одержана остаточна формула задає функцію . Отже, задана функція є самодвоїстою.

Рівність можна також перевірити за таблицею істинності:

Одержані значення підтверджують самодвоїстість функції .

Приклад 2.14. Дано логічну функцію . Побудувати таблицю істинності для двоїстої функції, записати формули двоїстої функції , використовуючи визначення двоїстості і принцип двоїстості, а також перевірити правильність побудови двоїстих формул. Встановити, чи є задана функція самодвоїстою.

Побудуємо таблицю істинності двоїстої функції на основі таблиці істинності заданої функції:

Запишемо формулу функції, двоїстої до , використовуючи визначення двоїстості: . Отже:

.

Відповідно до принципу двоїстості, замінюючи елементарні функції двоїстими, матимемо:

.

Використовуючи таблиці істинності, покажемо, що обидві одержані формули визначають функцію, двоїсту до заданої:

Побудовані таблиці істинності підтверджують припущення.