2.3 Системы с неограниченной растворимостью компонентов в жидком состоянии и ограниченной растворимостью в твердом состоянии

Описание диаграммы: Линия аЕb – линия ликвидуса, асЕdb – линия солидуса.

Области:

1. – расплав.

2. – равновесие расплава с твердым раствором В в А. В точке М система с общим составом g₁ состоит из жидкости с составом g₁^ж и твердого раствора с составом g₁^тв . Относительные количества фаз находят по правилу рычага.

3. – расплав + твердый раствор А в В.

4. – твердый раствор В в А (фаза одна).

5. – твердый раствор А в В (фаза одна).

6. – равновесие твердого раствора В в А и твердого раствора А в В.

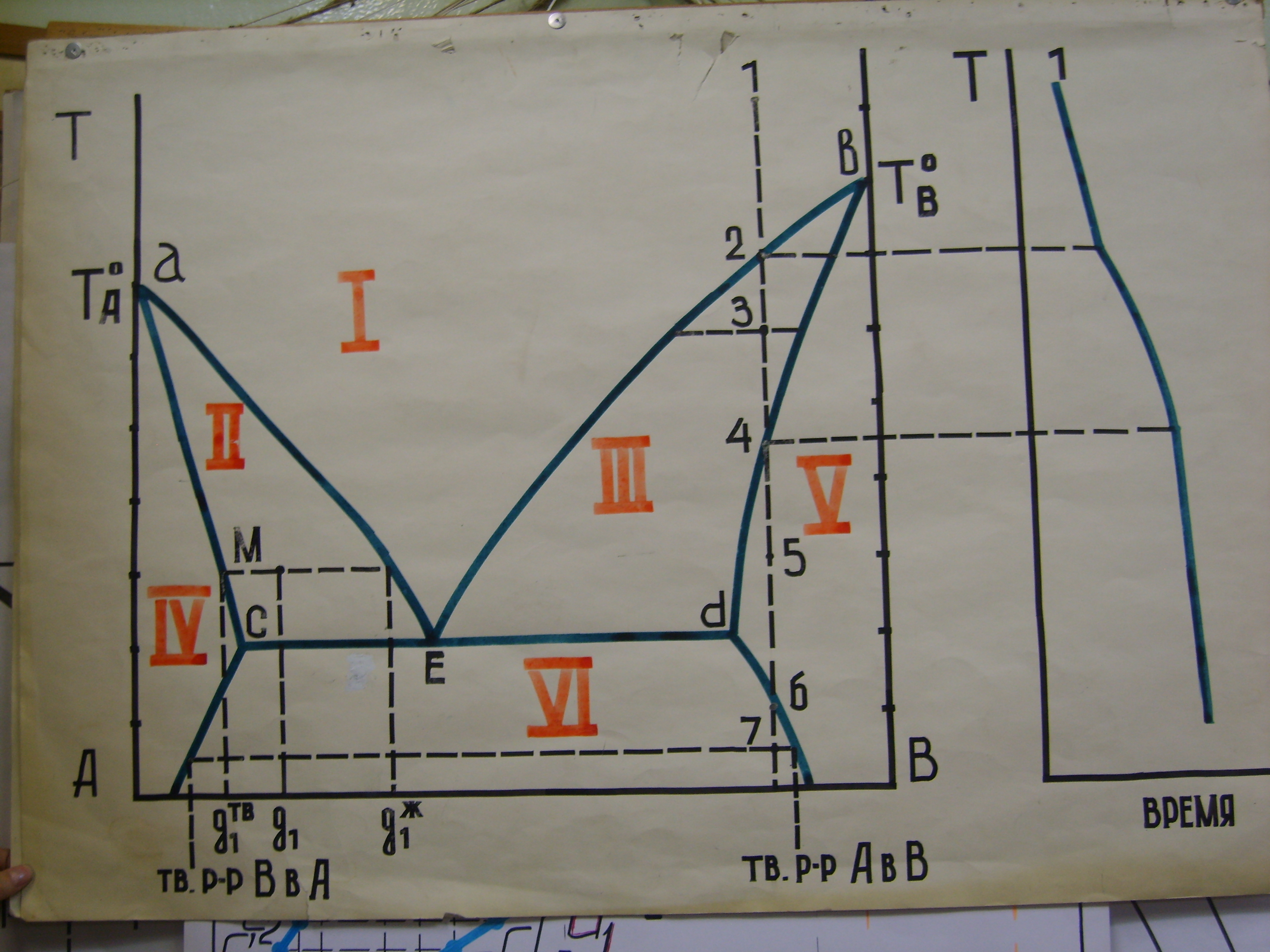
Рассмотрим процесс кристаллизации.

Точка 1: фаза одна – жидкая, С=2 – 1+1=2.

Точка 2: начало кристаллизации – выпадают кристаллы твердого раствора А в В. С=2 – 2+1=1, температура продолжает падать, выделяется теплота.

Точка 3: равновесие твердого раствора А в В и расплава. В ходе кристаллизации состав расплава меняется, меняется и состав твердой фазы (в том числе и состав ранее выпавших кристаллов, если это происходит медленно).

Точка 4: конец кристаллизации, фаза одна (твердый раствор А в В).

Точка 5: фаза одна, состав фазы не изменяется.

Точка 6: начинается уменьшение растворимости А в В в твердой фазе, выделяются кристаллы твердого раствора В в А.

Точка 7: равновесие твердого раствора А в В и твердого раствора В в А.

2.4 Системы с неограниченной растворимостью компонентов и в жидкой и в твердой фазе

Твердые растворы – изоморфные системы (одинаковая форма кристалла). Изоморфизм – свойство атомов или ионов замещать друг друга в кристаллических решетках.

Пример: система Cu – Ni:

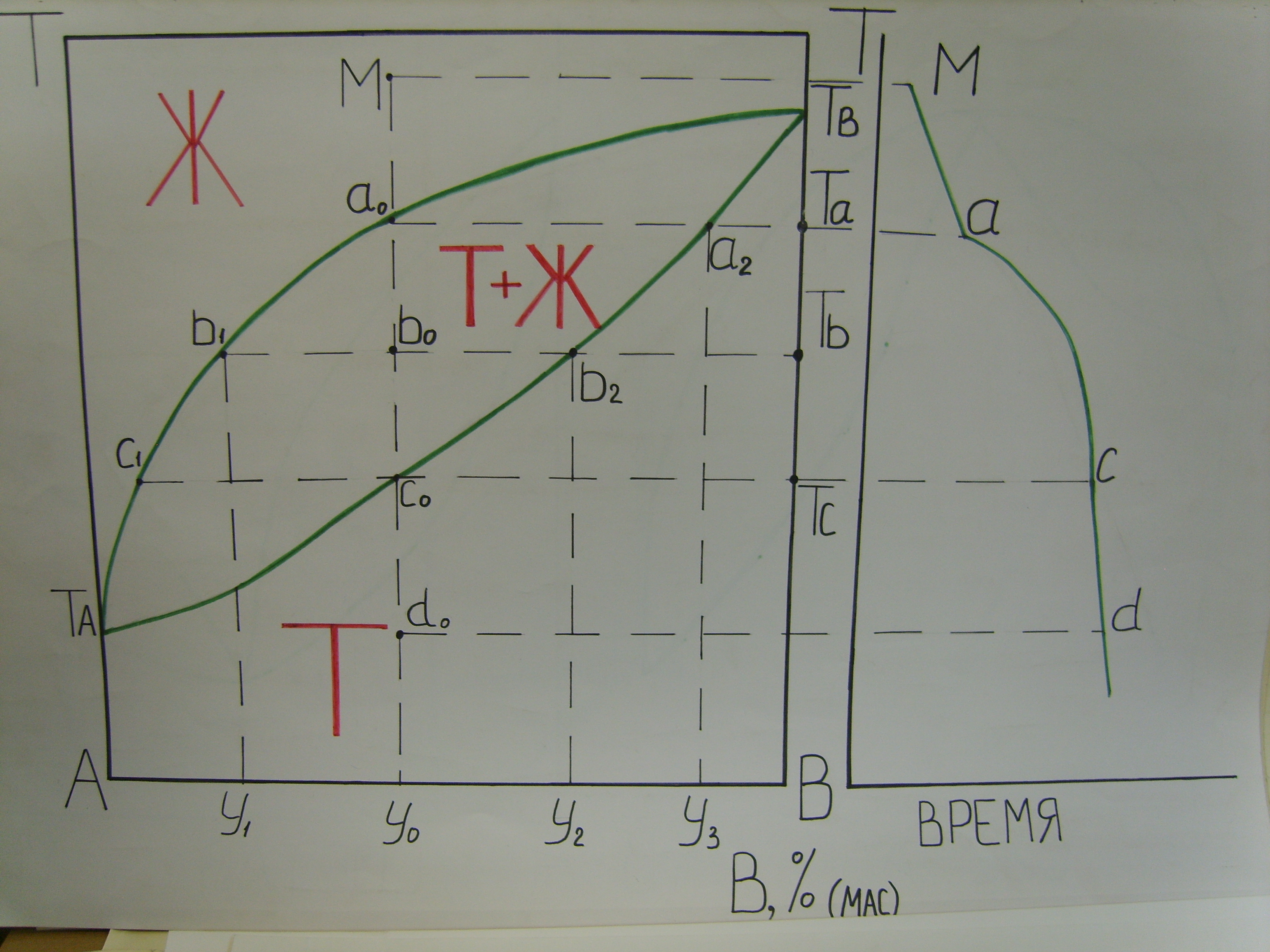
Описание диаграммы: верхняя линия – линия ликвидуса, выше нее система находится в жидком состоянии. Нижняя линия – линия солидуса, ниже нее система находится в твердом состоянии.

Области:

I – расплав,

II – расплав + кристаллы твердого раствора,

III – твердый раствор.

Рассмотрим процесс кристаллизации из точки М. Начинается кристаллизация в точке a . Выпадают кристаллы твердого раствора с составом, соответствующим точке a (у ). В ходе кристаллизации состав расплава изменяется, изменяется и состав твердой фазы; заканчивается кристаллизация в точке с . Все кристаллы имеют состав у . В твердой фазе можно получить кристаллы любого состава, поэтому эти компоненты неограниченно растворимы в твердой фазе.

3. Трёхкомпонентные системы

3.1 Графическое изображение состава трехкомпонентных систем

Для описания состояния трехкомпонентной системы нужно задавать 4 параметра: р, Т, х , х . Изобразить состояние такой системы можно в четырехмерном пространстве. Если рассматривать систему при постоянном давлении, то задавать нужно 3 параметра. Изобразить состояние системы можно на трехмерной диаграмме. Если рассматривать при постоянных давлении и температуре, то задавать нужно 2 параметра: х , х , а изобразить состояние можно на плоской диаграмме, при этом условное число степеней свободы: С_усл=3 – Ф. Можно изображать состояние системы в прямоугольных координатах, чаще пользуются треугольными диаграммами.

Треугольник состава

Треугольник АВС - равносторонний.

Точки А, В и С изображают чистые компоненты. Линии АВ, ВС и СА изображают двухкомпонентные системы. Точки внутри треугольника изображают трехкомпонентные системы. Для определения состава используют один из двух методов.

1. Метод Гиббса. Он основан на свойстве равностороннего треугольника: сумма длин перпендикуляров, опущенных на стороны из любой точки внутри треугольника, равна высоте треугольника:

РНа+ РНв+РНс=Сс.

Чтобы определить концентрацию компонента А в системе, состав которой изображается точкой Р, нужно провести из точки Р перпендикуляр на сторону противолежащую вершине А и определить какую долю его длина состовляет от высоты треугольника. Для удобства можно высоту разделить на 10 частей и нанести шкалу на одной из сторон треугольника.

Например, в точке Р: .

Метод Розебума. Он основан на свойстве равностороннего треугольника: сумма длин отрезков, проведенных параллельно каждой стороне треугольника из любой точки внутри треугольника равна длине стороны треугольника. Для того, чтобы определить концентрацию компонента А в системе, состав которой изображается точкой Р, нужно из этой точки провести прямую до пересечения с противолежащей стороной по отношению к вершине А параллельно одной из двух других сторон и определить, какую долю длина полученного отрезка прямой состовляет от длины стороны треугольника: .

Свойства треугольника состава

1. На линии LM: [В]=const. Точки на линии, параллельной стороне треугольника, соответствуют постоянной концентрации компонента, изображаемого противолежащей вершиной треугольника.

2. На линии BQ: . Точки на линии, проведенной из вершины, изображающей один из компонентов, соответствуют постоянному отношению концентраций двух других компонентов.