Логическое следствие и логический вывод

С помощью понятия модельной структуры уточняется понятие логического следствия, которое является интуитивно достаточно ясным. Пусть Я и р — про­извольное множество замкнутых формул и произвольная замкнутая формула, записанные в сигнатуре 2. Говорят, что 0 логически следует из Q, и пишут Q]=P, если р истинно во всякой модельной структуре для Я. Иными слова­ми, отношение логического следствия Я|— р имеет место тогда и только тогда, когда нет ни одной интерпретации, в которой все формулы из Я были бы ис­тинны, а формула р ложна. Таким образом, символ |= имеет двоякое употреб­ление: для обозначения отношения Af|=P между структурой и формулой н для обозначения отношения Я|=р между множеством формул и формулой.

19

Например, рассмотрим следующее утверждение:

Утв1—Операция оперЗ выполнялась на фрезерном станке. Очевидно, что Утв1 логически следует из Зн7 и Зн8. Утв1 формально представляется так;

тип-ст (ст (оперЗ)) = фрез. (18)

Поэтому неформальное логическое следствие Утв1 из Зн7 и Зн8 формально представляется в виде

(16), (17)| = (18). (19)

(Правильнее следовало бы писать {(16), (17)}|*=(18), но обычно фигурные скобки здесь не пишутся.)

Справедливость логического следствия (19) можно доказать математиче­ски. Пусть в некоторой структуре М истинны формулы (16) и (17), т. е. М\ = | = (16) и Af| = (17). Из последнего соотношения следует, что (см. П8)

М| = (дет(олерЗ)«=дет2), М\~(ст(оперЗ)=стЗ), Л7| = (нач(оперЗ)=5), ЛГ|=(нач(оперЗ) = 10).

В частности, формула ст(оперЗ) =стЗ истинна в структуре М. Отсюда следу­ет, что в М истинна также формула тип_ст(ст(оперЗ)) =тип_ст(стЗ). С дру­гой стороны, так как в М истинна формула, тип_ст(стЗ) =фрез, в М также истинна формула тшт_ст(ст(оперЗ))=фрез₁ т. е. М\ — (18). Итак, во всякой структуре М, в которой истинны (16) и (17), будет также истинна и (18). Следовательно,-(16), (17)|=*(18).

Для исчисления предикатов основной является проблема логического след­ствия: разработать методы и алгоритмы, позволяющие для произвольных Q и Р~ множества замкнутых формул и замкнутой формулы — выяснить, имеет ли место отношение логического следствия Q|=J3.

Проблема логического следствия эквивалентна проблеме логической невы­полнимости: разработать методы и алгоритмы, позволяющие для произволь­ного множества £2 замкнутых формул выяснять, является ли п невыполнимым множеством. Действительно, Q|=P имеет место тогда и только тогда, когда множество Q[}{ I P) невыполнимо. Докажем последнее утверждение. По опре­делению й|=р имеет место тогда и только тогда, когда нет ни одной струк^ туры М, такой, что для всех aeQ верно М\=а, но неверно, что jW|—р\ т. е. верно, что М \ = ~1 р. Последнее означает, что нет ни одной структуры М, такой, что М\=у для всех vsQU{"1P}. т. е. множество fiU{~lP) невыполнимо.

Проблема логического следствия тесно связана также с проблемой обще­ значимости логических формул. Замкнутая формула «G^¹ называется об­ щезначимой (или торжественно истинной), если а истинна во всякой структу­ ре сигнатуры 2. Очевидно, что соотношение ссь а% а_р|=р имеет место тог­ да и только тогда, когда формула о._х/\а₂/\ ... /\а_р-+$ общезначима. В самом деле, указанное логическое следствие справедливо тогда и только тогда, когда нет ни одной структуры М, такой, что jW|=aj, M|=?a2,...,M\~a_Vi и не имеет ме­ ста jW|—Р, а это означает, что нет ни одной структуры М, такой, что не име­ ет места М\=<х\/\аг/\ ■■■ Лар-Н*. Очевидно, что соотношение cti, аъ..-,а_р|=Р справедливо тогда и только тогда, когда формула aiA^A -Л'1?> невыполни­ ма, т. е. не имеет модельных структур.

А. Черч доказал алгоритмическую неразрешимость проблемы общезначи­мости формул исчисления предикатов: нельзя построить алгоритм, который был бы применим к любой замкнутой формуле а в произвольной сигнатуре и ко­торый выяснял бы, является а общезначимой формулой или нет. Теорема Чер-ча не запрещает существования алгоритмов общезначимости для отдельных сигнатур или классов сигнатур. Однако имеются сигнатуры с неразрешимой проблемой общезначимости.

В математической логике известна теорема Геделя, из которой следует, что можно построить частичный (т. е. «зацикливающийся» на некоторых предъяв­ляемых ему формулах) алгоритм, область определенности которого (т. е. мно-

20

жество формул, на которых он дает результат) включает множество всех обще­значимых формул. Теорема Геделя утверждает, что проблему общезначимости для исчисления предикатов можно решить с помощью системы логического вывода (дедукции) так называемого гильбертовского типа.

Система дедукции гильбертовского типа состоит из аксиом и правил вы­вода. Аксиомами служат некоторые общезначимые формулы. Правило выво­да—это отношение /?(а_ь а₂, ...,а_п) между формулами а_} (чаще всего п=2 или я~3), обладающее так называемым свойством состоятельности: если фор­мулы аь ссг,..,.,се„_1 истинны в какой-либо структуре М и имеет место R(an а₃,..., а„), то формула а_п также истинна в М.

Вместо R( аь аг,..., «_п) обычно пишут а_ь аг. •-» ctn-ij—ое_п и говорят, что

формула а_п получена из формул аь аг a_n-i применением к ним правила

вывода R. Выводом формулы Р из множества формул Q называется последова­тельность формул, такая, что ее последняя формула совпадает ери каждая другая формула либо есть аксиома, либо получается применением к некото­рым предыдущим формулам одного из правил вывода. Если существует вывод формулы р из множества формул £3, то говорят, что р выводима из п, и пи­шут й HP-Система дедукции называется полной, если для любого множества формул Q формула р выводима из Q тогда и только тогда, когда Р логически следует из п, т. е. Q\~ р тогда и только тогда, когда Q|=p. Теорема Геделя устанав­ливает факт полноты некоторой системы дедукции.

Для практических задач теории логических моделей представления знаний более эффективны системы дедукции не гильбертовского, а резолюционного типа (§ 2.4).

Проблемы логического следования и логической невыполнимости важны не только для исчисления предикатов, но и для других формализмов представле­ния знаний.

Пусть Д—какое-либо описание предметной области в некотором форма­лизме представления знаний. Если этот формализм является логическим язы­ком, то Д есть логическая модель предметной области. Д состоит из двух ча­стей: Д' и А", которые описывают соответственно структурные свойства пред­метной области и логические ее свойства. (Например, если формализмом пред­ставления знаний является многосортное исчисление предикатов, часть Д' есть сигнатура 2, а часть А" — совокупность замкнутых формул fi, записанных в сигнатуре 2.) Часть А" служит для представления ограничений, которым удовлетворяют сущности и отношения предметной области, закономерностей, описывающих поведение сущностей, и т. п.

Цель разработки логической модели — получить такое описание Д, чтобы его часть А" .имела модельную структуру М, формально приближающую за­данную предметную область. Но разработчик логической модели может со­вершить ошибки, в результате которых А" не будет иметь модельных струк­тур, адекватных предметной области. Ошибки могут быть столь критичными, что А" вообще может не иметь модельных структур. Ясно, что методы выяс­нения невыполнимости могут быть использованы для обнаружения таких кри­тических ошибок.

Вопросы анализа предметной области после ее формализации могут быть сведены к выяснению соответствующих свойств модельных структур для Д. Многие из этих свойств удается представить предложениями того же логиче­ского языка, который был использован для составления описания Д. Если Р обозначает одно из таких предложений, то все модельные структуры для А" будут обладать свойством, выраженным в р, тогда и только тогда, когда Д"|=р. Таким образом, методы логического вывода могут быть полезны для решения задач анализа предметных областей.

Иногда разработчика интересует логическая модель Д, которая не содер­жит избыточной информации в том смысле, что из Д нельзя исключить ни од­ного предложения р, не изменив совокупности модельных структур. Очевидно, что р можно исключить из Д" тогда и только тогда, когда Д"}«=р. Таким об-

21

разом, методы логического вывода можно использовать для решения задачи избыточности информации.

Запросы информационно-справочного характера к базам данных, пред­ставляющим модельные структуры для логической модели, также можно трак­товать в терминах логического следования или невыполнимости. Пусть, напри­мер, запрос состоит в нахождении всех объектов (сущностей), которые обла­дают определенным свойством в предметной области. Часто свойство объектов удается выразить некоторым предложением fi[x] в логическом языке. Это предложение содержит свободную переменную х, вместо которой разрешается подставлять имена объектов (константы), среди которых разыскиваются обла­дающие заданным свойством. Таким образом, запрос можно сформулировать так: «Найти все константы с, такие, что предложение Д[с] истинно в заданной структуре ЛЬ, или в более формальном виде: «Найти множество {с\М\=$[с]}», Ответ на этот запрос может быть вычислен путем перебора всех констант с (данного сорта С) и отбора тех из них, для которых формула $[с] истинна в структуре М (последнее выясняется непосредственным применением правил П8 и П9). Но можно свести вычисление этого запроса к логическому выводу формулы

(у#е С) {Р [х] -* ответ (х)} (20)

из совокупности формул пм, которая однозначно характеризует структуру М. Формула (20) неформально выражает следующее: «Всякий раз, как какая-ли­бо константа сорта С удовлетворяет формуле Р, считать ее ответом». Совокуп­ность Qw состоит из тех константных формул вида f(c\, C2,...,c_n)~c или p(ci, Ci,...,c_n), которые истинны в М. Заметим, что полные методы дедукции могут быть модифицированы так, что из вывода (20) можно извлечь все кон­станты с, такие, что р[с] выводима из пм

Усилением рассмотренного запроса является запрос: «Найти все констан­ты с, для которых $[с] истинна во всех модельных структурах для Д"». Уси­ленный запрос состоит в нахождении множества {с|Д"|=р[с]}. Таким обра­зом, для вычисления ответа на этот запрос можно применять логический вывод.

Чаще, однако, рассматриваются запросы «промежуточного» типа, когдз структура, моделирующая предметную область, представлена лишь частично. Пусть Р обозначает частичную структуру, расширяемую до некоторой мо­дельной структуры для Д". Как правило, расширение Р неоднозначно, и за­прос формулируется тогда так: «Найти множество {c|Af|—p[c], M расширяет Р}>. Частичная структура Р также может быть охарактеризована конечным множеством Qp константных формул. Ясно, что запрос эквивалентен запросу: «Найти {<?|A"UQp|=p[cJ}», Д^дя вычисления которого снова можно применить метод логического вывода.

Логические языки и модели данных

В теории баз данных под моделью данных понимают формализм, предна­значенный для описания структур данных, зависимостей между ними, а также так называемых ограничений целостности, т. е. некоторых условий, которым должны удовлетворять допустимые базы данных. Описание, выполненное в та­ком формализме, называется схемой. Допустимая база данных, т. е. конечная совокупность данных, удовлетворяющих схеме, называется экземпляром схемы.

В указанной терминологии язык многосортного исчисления предикатов сле­дует считать моделью данных. В самом деле, 2{JQ можно рассматривать как схему, причем первая.ее часть (сигнатура 2) описывает структуру данных, а вторая часть (множество Q замкнутых формул) — зависимости и ограничения целостности. Конечную модельную структуру для Я можно считать экземпля­ром схемы 2(fl

22

Таблица 1.5

		т	а блица 1.7
	Станок
НомерСтанка			ТипСтанка
1 2 3			ТОК ТОК фрез

Операция

НомерДетали	НомерСтанка	Начало	Конец	ТнпОперации
1	3	0	5	фрез_торц
1	I	5	12	ТОК-Обр
2	3	5	10	фрез_торц
2	2	10	17	ток-обр
3	3	10	16	фрез_торц
3	1	16	24	ток_обр
4	3	16	22	фрез_торц
4	2	22	28	ток-обр

		т	а блиц а 1.6
	Деталь
НомерДетали			ТипДетали
1 2 3 4			ст_вал ст_вал вал „шест вал „шест

Реляционная модель данных [Codd, 1970]—это формализм, непосредст­венно соответствующий простому фрагменту языка многосортного исчисления. В качестве примера построим реляционную схему для данных фрагмента пред­метной области «механообработка». Экземпляр этой схемы показан в табл. 1.5—1.7.

В реляционную схему R включим три отношения, назвав их (как и рань­ше в примере сигнатуры 2) Деталь, Станок и Операция. Эти отношения име­ют атрибуты с именами НомерДетали, ТипДетали, НомерСтанка, ТипСтанка, ТипОггерация, Начало, Конец. Связь атрибутов с отношениями указана при помощи структурных предложений:

Деталь [НомерДетали, ТипДетали], Станок [НомерСтанка, ТипСтанка],

Операция [НомерДетали, НомерСтанка, Начало, Конец, ТипОперации]. Структурную часть R' реляционной схемы получаем, дописывая к этим струк­турным предложениям описания доменов (областей значений атрибутов):

dom (НомерДетали) = dom (НомерСтанка) = {1,2,3,...};

dom (ТипДетали) = {ст_вал, вал-шест};

dom (ТипСтанка) ={ток, фрез};

dom (Начало) = dom (Конец) = {0,1, 2,...};

dom(ТилОлерации) = {ток_обр, фрез_торц}.

Ясно видна связь структурной части R' реляционной схемы с сигнатурой 2=*{(1), (2) (9)}. Но непосредственно R' отвечает сигнатуре Su представ­ ленная следующими выражениями:

№-дет: Операция -»-НомерДетали №_ст: Операция->-НомерСтанка, нач: Операция -^-Начало, кон: Операция -»-Конец, тип_опер: Операция -»» ->ТнпОпераци/и, №_дет: Деталь -»-НомерДетали, тип_дет: Деталь-»-ТипДе-тали, №_ст: Станок ->НомерСтанка, тип_ст: Станок -*-ТипСтанка, фрез_торц: -»-ТинОперации, ток-обр:-^ТипОперации, ст-вал: -^ТипДетали, вал-шест: -*-ТипДетали, ток: -^ТипСтанка, фрез: -*-ТипСтанка, /: ~*-Но-

23

k: ->Начало, к: ->Конец (Ь

мерДетали, /: -^НомерСтанка

Сигнатура Si получается из R' трансляцией, при которой отношения и ат­рибуты реляционной схемы переходят в сорта сигнатуры, а каждая пара от­ношение— атрибут определяет одноместную функцию, отображающую элемен­ты сорта, соответствующего отношению, в элементы сорта, соответствующего атрибуту (например, пара Операция — НомерДетали определяет функцию Опе­рация ->НомерДетали, которая обозначена №~дет).

Предложения, задающие так называемые ключи и функциональные зави­симости, естественно отнести к логической части R" реляционной схемы R, Ключ— это набор атрибутов отношения, значения которых однозначно иден­тифицируют кортежи этого отношения (иначе, строки таблиц, представляющих отношение). В данном примере реляционной схемы имеем следующие предло­жения, задающие ключи:

НомерДетали ключ в Деталь, НомерСтанка ключ в Станок,

(НомерДетали, НомерСтанка) ключ в Операция.

Эти предложения просто выражаются в языке многосортного исчисления пре­дикатов. Например, для третьего предложения имеем формулу

(V^х- у€= Операция). (№.„дет_оп (х) = №_дет_оп (у)) А (№_ст (х) = №_ст (у)) -> х = у.

Функциональная зависимость — это связь между набором атрибутов отно­шения и другим его атрибутом, определяющая ограничение на экземпляры схемы: в каждом кортеже значения атрибутов из набора однозначно опреде­ляют значение другого атрибута. Функциональная зависимость выражается предложением вида

(21)

(Аи А₂ А_р) определяют В в С,

где Аи А₂,..., А_р, В — атрибуты отношения С. Например, имеем

НомерСтанка определяет ТипОперации в Операция.

Функциональные зависимости также можно отнести к логической части R" реляционной схемы. Они выражаются простыми формулами многосортного ис­числения предикатов. Например, (21) представляется формулой (Ух, у) Операция).(№_ст(*)=№_ст(у)-*-(тип_опер(д:) =тип_опер(у)).

Предложения реляционной схемы R, отличные от структурных предложе­ний, ключей и функциональных зависимостей, выражают ограничения целост­ности. Например, знание Зн2 следует отнгсти к ограничению целостности. В сигнатуре 2 Зн2 выражено формулой (И). В сигнатуре 2i это же знание выражается той же формулой, но с заменой имени Время на имя Начало или Конец (так как в 2 первое имя отсутствует, а второе и третье имена входят в Si и как сорта имеют ту же интерпретацию, что и первое имя).

Язык многосортного исчисления предикатов можно, таким образом, ис­пользовать в качестве формализма для записи ограничений целостности. В fCodd, I972] предложено языки запросов к реляционным базам данных стро­ить на основе исчисления предикатов.

Рассмотрим, например, следующий запрос к базе данных, записанной в табл. 1.5—1.7: «Выдать номера деталей с указанием их типа, которые к мо­менту времени 20 прошли токарную обработку». Его можно сформулировать как нахождение множества

По методу Кодда этот запрос можно транслировать в последовательность опе­раций над отношениями (таблицами), которая состоит из операций проекции и так называемого естественного соединения. Выполнив эту последовательность операций, получим ответ на заданный запрос.

Метод Кодда фактически основан на теоретико-множественной трактовке правил П8 и П9, при которой, в частности, конъюнкции соответствует операция естественного соединения, а квантору g — операция проекции.

Запросы к реляционной базе данных можно вычислить с помощью логиче­ского вывода. Для этого предварительно базу данных D нужно представить совокупностью по атомарных константных формул вида f(c)=d, где / — имя функции, соответствующее паре отношение — атрибут, с — имя строки таблицы, a d — значение атрибута, стоящее в этой строке. Например, четвертая строка табл. 1.5 вносит в Qo такие атомарные константные формулы: №~дет(опер4) = =2, №_ст(опер4) =2, нач(опер4) = 10, кон(опер4) = 17.

Запрос (22) к базе данных D, представленной в табл. 1.5—1.7, вычисляет­ся с помощью вывода из Q_D формулы

(ух ^ НомерДетали,

Tim Детали) {Р[х, у] -* ответ (х, у)},

где J3[jc, у] обозначает входящую в (22) формулу.

Метод вычисления запросов, основанный на логическом выводе, является менее эффективным, чем метод Кодда и другие подобные методы прямого вы­числения запросов. Однако первый метод универсален и годится для вычисле­ния запросов к неполным базам данных, другие же прямые методы оказывают­ся непригодными.

Неполной базой данных называется такая база Е, которая не удовлетво­ряет зависимостям и ограничениям из R", но может быть расширена до до­пустимой базы данных D (т. е. базы данных, удовлетворяющей всем зависи­мостям и ограничениям из /?"). Запрос к неполной базе данных Е может быть вычислен с помощью логического вывода запросной формулы из сово­купности формул Ue[}R".

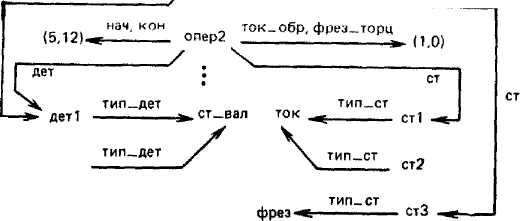
Произвольную сигнатуру S в языке многосортного исчисления предикатов можно представить графически, как это показано на рис. 1.1 для сигнатуры 2={(1), (2),..., (9)}. Сигнатуры, интерпретирующие сигнатуру S, также мо­гут быть представлены графически, как это видно из рис. 1.2, где показан фрагмент сети, представляющий информацию, записанную в табл. 1.2—1.4. Та­ким образом, рис. 1.1 играет роль схемы, а рис. 1.2 — роль экземпляра этой схемы.

Язык сетевых схем и сетей-экземпляров указанного типа называют бинар­ной моделью данных. Бинарную модель называют также функциональной мо­делью. Заметим, однако, что в бинарной модели используются только одно-

нач, кон ток_обр, фрез Время -^ Операция ?». Т

дет

/

Станок

Деталь

тип—дет

ТипСтанка

ТипДетали

{(*» у) I (агGОперация). (Ж_дет_оп (г) = х) Л

(тип_опер (г) = ток_обр) Д

(кон (г) > 20) А

(3"&Деталь). (тип_дет (а) — у) Д

(№_ дет (и) = х)> 24

(22)

dom (ТипДетали) « {ст_мл, вал-шест]>, dom (ТипСтанка) ={ток, фрез} dom (Времн) ={0,1,2,...}, dom (T) ={o, i}

Рис. 1.1

25

^Ha4'^KOH one_Pi ток-обр, фреэ^торц \

дет2

дет

Рис. 1.2

местные функции и предикаты. Чтобы представить в бинарной модели много­местные функции или предикаты, нужно прибегать к искусственному приему, вводя дополнительные имена сортов (классов). Так, «-местную функцию f : AiX ХА2Х ... ХА_п-*~В можно заменить на (2я+1) одноместных функций f;C->*B, gj-.Aj -+С, hj: С -*-А_} (1</<я), где hj~ функция проекции декартова произ­ведения на /-ю его компоненту, ^- — функция вложения /-й компоненты в де­картово произведение.

Имеется тривиальный прием перевода л-местной функции в (я-И)-местный

предикат: f(x_h х₂,...,х_п)=у тогда и только тогда, когда предикат }{х_х х_п,у)

истинен. Благодаря этому «чистое» (т. е. без функций) исчисление предикатов эквивалентно с точки зрения принципиальной выразительности многосортному исчислению предикатов.

Реляционная модель данных, естественно, переводится в «чистое» исчисле­ние предикатов. Рассмотрим снова пример реляционной схемы R, который свя­зан с предметной областью «механообработка». Получаемая «чисто» предикат­ная модель данных, обозначаемая Q, составляется из двух частей: структурной части Q' и логической части Q". Структурная часть соответствует «шапкам» таблиц-реляций: Q'= {операция(№_детали, №_станка, Начало, Конец, ТипОперации),

деталь (№_детали, ТипДетали), станок (№_станка, ТипСтанка)}. В логическую часть включаются предложения, выражающие ключи и функ­циональные зависимости. Например, в Q" записываем предложения

U= V: — операция (.V, У, U, _,_), операция (X, Y, V, _, _), (23)

U=V: —операция (X, У, _,£/,_), операция (А', У, _, V, _), (24)

U~ У '— операция (X, У_, _, U), операция (X, Y, _, _, V), (25)

U = V : — операция ( —., X, ^, _, U), операция (_, X, „, _, V). (26)

Предложения (23)—(25), взятые вместе, выражают то, что (№_детали, №-стаика) является ключом отношения «операция», а дредложение (26) вы­ражает то, что ТипОперации функционально зависит от №_<ст в отношении «операция».

В предикатной схеме Q использовался синтаксис языка логического прог­раммирования Пролог [Клоксин и др,, 1987], идеи которого были выдвинуты в [Kowalski, 1974]. Согласно этому синтаксису имена отношений, функций и констант пишутся малыми буквами, а переменные начинаются с заглавных букв. Знак :— является символом импликации, но записанной справа налево <<-); запятая служит символом конъюнкции. Предложения (23)—(26) явля­ются примерами так называемых правил. В правилах неявно предполагается,

26

что все переменные связаны квантором у. Таким образом, например, предло­жение (23) в обычной нотации выглядит гак:

№_ детали, уУ&№_ станка, yt/еНачало, уК^Начало, yZl e Конец, у22е Конец, yZ3& ТипОперации, у24&ТипОперации).

■операция (X, Y, U, Zl, Z2) Доперация (X, Y, V, 23, Z4)->£/= V.

Экземпляр предикатной схемы Q представляется списком так называемых фактов, т. е. атомарных константных формул. В данном примере имеем такой экземпляр (предикатную базу данных F):

операция (1,3, операция (1, 1, операция (2,3, операция (2, 2, операция (3,3, операция (3,1, операция (4,3, операция(4. 2,

О, 5, фрез_торц). 5,12, ток_обр). 5, 10, фрез_торц). 10, 17, ток_обр). 10, 16, фрез_торц), 16, 24, ток-обр). 16,22, фрез_торц). 22, 28, ток_обр).

деталь(1, ст-вал). деталь (2, ст_вал). деталь (3, вал-шест). деталь(4. вал-шест), станок(I, ток), станок(2, ток), станок(3, фрез).

Рассмотрим снова запрос: «Выдать номера деталей с указанием их типов, которые к моменту времени 20 прошли токарную обработку», обратив его к предикатной базе данных F. Этот запрос вычисляется с помощью правила

ответ[X, Y) : — операция(X, V, Z, V, ток-обр), £/>20, деталь(X, У). (27)

Вычисление запроса инициируется предложением ? — ответ (X, Y), которое фор­мирует цель: «Найти факт, унифицируемый с ответ(X, У)». Делая попытку до­стижения этой цели непосредственно, интерпретатор начинает просмотр базы фактов F, но, не найдя подходящего факта, обращается к базе правил, пыта­ясь найти такое, которое имеет «голову», унифицируемую с ответ(X, У). Та­ким правилом является (27), из которого получается цель:

«Найти факт, унифицируемый с операция(X, V, Z, U, ток-обр)». (28)

На этот раз цель удовлетворяется при подстановке X=l, V=l, Z=5, Z=12 (см. второй факт в F). Теперь формируется цель, состоящая в выяснении не­равенства 12^=20, получаемого из второго атома «хвоста» (27) при найденной подстановке. Так как это неравенство неверно, подстановка отменяется и ин­терпретатор снова пытается удовлетворить цель (28), производя поиск в F с точки возврата. Цель удовлетворяется при подстановке Х=2, V=2, Z=10, U'=17 (см. четвертый факт в F). Однако опять получается неверное неравен­ство 17^20, и процесс поиска возвращается с отменой подстановки и выдви­жением цели (28). Шестой факт из F удовлетворяет этой цели с унифицирую­щей подстановкой ^=3, V=\, Z=16, £/=24. Так как неравенство 24>20 варно, то формируется очередная цель: «Найти факт, унифицируемый с де­таль (3, У)», которая удовлетворяется при подстановке У-вал-шест. Поскольку цели, ассоциированные с «хвостом» правила (27), удовлетворены при подста­новке ЛГ=?Д К=1, Z=16, £/=24, У=вал-шест, то получим вычисленный факт ответ(3, вал-шест). Процесс поиска продолжается по той же схеме. В резуль­тате имеем еще один вычисленный факт ответ(4, вал-шест).

Итак, основанная на «чистом» Прологе предикатная модель Q[}F характе­ ризуется следующими чертами: (1) структурная часть Q' схемы Q составля­ ется из предложений простейшего вида, задающих схему отношений; (2) логи­ ческая часть Q" схемы Q составляется из правил, т. е. предложений вида В:—Аи А₂ А_п, где В, А/ — предикатно-атомарные формулы; (3) кроме де­ кларативной интерпретации («если одновременно истинны все А), то истинно В») правило имеет простую процедурную интерпретацию («чтобы достичь це­ ли В, нужно одновременно достичь все цели Л/»); (4) достижение нескольких целей осуществляется с помощью механизмов унификации и поиска с возвра­ том; (5) запрос к базе данных F записывается в виде правила ответ (Хи Хг,— ...,Х_р): — Ai, А₂,...,А_п, а вычисление запроса инициируется предложением

?—ответ(*_ь Х₃ Х_Р).

27

Краткая история и современные тенденции

Исчисление предикатов было создано усилиями Г. Фреге (1879 г.), К. Пир­са (1885 г.), Дж Пеано (1908 г.), А, Н. Уайтхеда и Б. Рассела (1922—1927гг.) для формального описания математического знания в связи с попытками ре­шения проблем основания математики. Формальная семантика исчисления пре­дикатов, основанная на теоретико-множественных моделях, была предложена А. Тарским (1930 г.). Полная система дедукции разработана Д. Гильбертом, П. Бернайсом и В. Аккерманом (1922—1928 гг.), а ее полнота доказана К. Ге-делем (1930 г.).

Г. Саймон, А. Ньюэлл и Дж. Шоу написали в 1957 г. машинную програм­му «Логик-теоретик», выполняющую поиск доказательств тавтологий в аксио­матической системе Рассела — Уайтхеда для пропозиционального исчисления. Первая серьезная попытка построить машинную систему для поиска логическо­го вывода в исчислении предикатов была предпринята в 1958 г. [Ван Хао, ' J970]. Важные результаты для создания эффективных систем логического вы­вода революционного типа были получены в 1963 г, [Девис, 1970] (§ 2.4).

Первая вопросно-ответная система, использующая дедукцию резолюцион-ного типа [Green, 1969], является прообразом современных «интеллектуаль­ных» информационных систем (систем дедуктивных баз данных и баз зна­ний). Рь работка и применение логических моделей для баз данных и баз зна­ний описаны в [Gallaire et al., 1978].

В [Hewitt, 1971; Kowalski, 1974] была замечена двойственность семантики импликации: имлликация рЛЯ~*-^г имеет, с одной стороны, логическую трактов­ку (так называемая «материальная импликация»), с другой стороны, операци­онную (или процедур а л ьную) трактовку («если вы хотите установить г, пы­тайтесь установить р и q»). Импликации с универсально квантифицированными переменными (связанными только кванторами V) называют также хорнов-скими предложениями. Благодаря указанной операционной трактовке последо­вательность хорновосих предложений можно рассматривать как некоторую недетерминированную программу. Детерминизация процесса вычисления по та­кой программе достигается поиском с возвратом. Эти простые, но фундамен­тальные идеи были положены в основу языков логического программирования (Плэннер, Пролог и др.).

Логические модели, построенные с применением языков логического прог­раммирования, широко применяются в базах знаний, экспертных системах. Практическое использование логических моделей облегчается выбором удачно­го синтаксиса языка логического программирования, а также включением в язык различных абстракций, таких как агрегация, таксономия, родовидовое отношение, наследование свойств и т. п. Для усиления практической вырази­тельности логических моделей важна также объектная направленность языков представления знаний, так как неформальное описание предметных областей эксперты выполняют в терминах объектов, их связей и динамики. Разработка объектно-ориентированных языков программирования представляется весьма перспективным направлением исследований.