Резолюция с абстракцией

Методы доказательства теорем, основанные на абстракции, были предло­жены в [Plaisted, 1981], где использовалась идея аналогии, заключающаяся в том, что данная проблема А преобразуется в более простую проблему В, Далее, если А имеет решения, то и В имеет решения, причем структура одного из решений для В аналогична структуре решений для А. Поэтому решения для

97 4-6943

В можно использовать как руководство в поиске решений для А, Конечно, может случиться, что В имеет решения, даже если А их не имеет.

Как и раньше, полагаем, что дизъюнкт С, поглощает дизъюнкт С₂, если имеется подстановка в, такая, что CYEJeCa (6\9 называется примером дизъ­юнкта Си если 9 — константная подстановка, то Cfi называется фундаменталь­ным примером дизъюнкта С\).

Абстракцией называется соотнесение множества дизъюнктов /(С) с любым дизъюнктом С, таким, что / обладает следующими свойствами: 1) если дизъ­юнкт Сз является резольвентой дизъюнктов Су и С₂ и /?₃е/(С₃), то сущест­вуют Di^f(Ci) и £>₂е/(С₂), такие, что некоторая резольвента дизъюнктов А и D₂ поглощает D₃; 2) /(П) = {П}; 3) если C_t поглощает С₂, то для любой абстракции D₂ дизъюнкта С₂ имеется абстракция Д дизъюнкта Си такая, что D\ поглощает D₂. Если / является отображением, обладающим этими свойства­ми, то оно называется отображением абстракций. Если £>е/(С), то D называ­ется абстракцией дизъюнкта С. Абстракции обычно удовлетворяют свойству, что любой D в /(С) является тавтологией, если дизъюнкт С — тавтология.

Для конструирования абстракций в [Plai.sted, 1981] доказана следующая теорема. Пусть F— множество отображений литер на литеры. Предположим, что для всех OeF и для всех литер L имеет место Ф(~]Ц— |Ф(£).Если

С —дизъюнкт, то Ф(С) = {Ф(£) : Z,eC}. Предположим также, что если дизъ­юнкт D является примером дизъюнкта С, то для всех Ф^еР существует Ф\^Р, такое, что Фг(") является примером <Ь\{С). Определим / через /(С)= = {Ф(С) : Фе/⁷}. Тогда / является отображением абстракции.

Имеются синтаксические и семантические абстракции. Примерами синтак­сических абстракций служат фундаментальная абстракция, пропозициональная абстракция, абстракции, связанные с переименованием предикатных и функцио­нальных букв, с изменением знака литер, с перестановкой и вычеркиванием некоторых аргументов у предикатов или функций. Если С — дизъюнкт, то f(C) = {C':C является фундаментальным примером для С) есть фундамен­тальная абстракция.

Пропозициональная абстракция определяется следующим образом. Пусть С —дизъюнкт вида L\\JL%\' .:.\/Lk. Тогда f(C) есть {С}, где С — дизъюнкт вила WX«'V ... VW и L_t'(l<i<k) есть Р, если L_t есть P(t_u t₂,...,t_n), и IP, если L_{ есть ~\P(tt, t₂,...,t_n), т. е, получаем дизъюнкты для исчисления высказываний. Специальным случаем этой абстракции является абстракция, связанная с вычеркиванием переменных (необязательно всех).

Если в дизъюнктах переименовать некоторым систематическим образом предикатные и функциональные буквы, то получится абстракция с переимено­ванием.

Аналогично, меняя знаки литер или переставляя аргументы у функциональ­ных н предикатных букв, имеем соответствующий тип синтаксической абст­ракции.

Семантическая абстракция связана с интерпретацией множества дизъюнк­тов, в котором означиваются все переменные функций и предикатов.

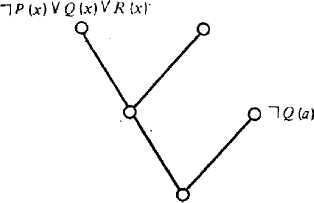
Покажем на примерах, как используются абстракции при доказательстве. Рассмотрим доказательство R(a) на дереве вывода (рис. 2.6,а) и с помощью пропозициональной абстракции (рнс. 2.6,6). Однако, применяя эту же пропо­зициональную абстракцию к доказательству другого дизъюнкта, получаем дока­зательство, неадекватное исходному, как это будет видно из следующего примера.

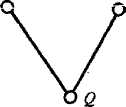
Для дерева вывода (рис. 2.7,а) применяем пропозициональную абстракцию. Получаем дерево вывода на рис. 2.7,6. Здесь имеет место потеря литеры ~~\Р(6). Во избежание таких потерь используем понятие мультидизъюнкта, в котором одна и та же литера может встречаться более одного раза, т. е., например, для дизъюнкта ~lP(a)V~l£4*)VQ(£) мультндизъюнкт, полученный пропозициональной абстракцией, будет иметь вид 1 PV ^PVQ- Тогда, продол­жая пример и используя понятие мультнднзъкжкта, нетрудно получить вывод QVR. 98

R (а)

QVR

Q(x)VR{x)

Р (х)

1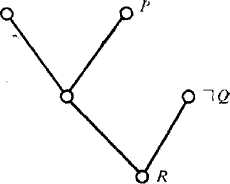 PVQVR

1PVQ

Р(а)

Р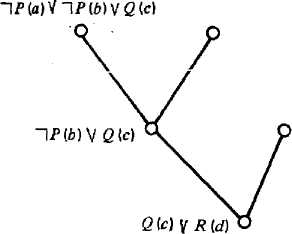 ис. 2.6

Pib)\jR(d)

6)

Рис. 2.7

Таким образом, доказательство с абстракциями дает как бы путь для до­казательства теорем, идя по которому мы восстанавливаем исходные дизъюнк­ты и, реэольвируя их, получаем доказательство теоремы. Естественно, что не все пути, построенные таким образом, будут приводить к нужному результату.

В [Plaisted, 1981] было разработано несколько вариантов полных алгорит­мов доказательства теорем, основанных на абстракциях.

Вывод для формул, представленных в матричном виде

Методы дедуктивного вывода для формул, представленных в матричном виде, были предложены в [Andrews, 1981]. Особенностью этих методов выво­да является преобразование формулы в негативную нормальную форму (ННФ), которая затем представляется в матричном виде. Будем говорить, что формула F находится в ННФ тогда и только тогда, когда каждое вхождение знака от­рицания в F атомарно, т. е. отрицание стоит перед атомом.

Так как при доказательстве может потребоваться несколько примеров од­ной и той же подформулы, введем понятие квантифицированного удвоения. Формула R' получается из формулы R посредством квантифицированного уд­воения тогда и только тогда, когда R^f является результатом замены некоторой подформулы в R вида ухМ на ухМ&ухМ. Все переменные, стоящие под знаком квантора, должны быть отмечены различными буквами, т. е. & ууМ.

99

F¹:

Формулу F будем называть расширением ис­ходной формулы R, если она получена из R после­довательностью квантифицированных удвоений, пере­именованием различными буквами всех переменных, стоящих под знаками кванторов, и удалением кван­торов из R (кванторы существования удаляются ско-лемизацией).

Бескванторная формула необязательно должна быть представлена в КНФ. Она может иметь про­извольный вид, приведенный к базису ~~\ , \/, &.

Рис. 2.8

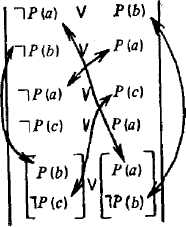
Для удобства представим формулу в виде матрицы таким образом, что дизъюнкты расположе­ны по горизонтали, а конъюнкты (т. е. наборы литер, соединенных конъюнкциями) — по вертикали. Напри­мер, формула

V Р(У)) & П ^р{У) V Р (<*)))& (П P(a)VP(w)) & П P(w) V Р(а))) & ((Р(Ь)& 1 Р(с)) V (PU) & 1 Р(х)))

в матричной форме имеет вид

(1)

-\Р(а) V Р{у) 1 Р(у) V Р(а) 1 Р(я) V "1 Р(») V Р(Ь) 1 ., Г Р(г)

_bZH

Сцепкой М для формулы F называется бинарное отношение на множестве вхождений литер в F, такое, что имеется подстановка 6, такая, что L$ = = 1 L₂6 всякий раз, когда' LiML₂, где Ц и L₂ — сцепленные литеры. Сцепка М является сцепкой опровержения для F тогда и только тогда, когда F ложна относительно любого приписывания истинностных значений атомам, т. е. когда F не имеет модели.

Для матрицы (1) найдем такие подстановки 0, которые делают формулу F невыполнимой (противоречивой). В итоге получим матрицу (для удобства сцепку изобразим в виде линий, соединяющих сцепленные литеры), показанную на рис. 2.8.

Вертикальный путь через матрицу — это последовательность литер форму­лы, которая содержит все литеры конъюнкции, если они встретились на этом пути, и одну литеру из дизъюнкции, если путь проходит через дизъюнкцию. Для матрицы (1) одним из таких вертикальных путей будет путь ~| Р(а), 1/>(*), ~\Р(а), 1Р(с), Р(Ь), -|Р(с).

Сцепка М является допустимой некоторым путем сцепкой (р-допустимой) тогда и только тогда, когда каждый вертикальный путь через матрицу содер­жит сцепленную пару литер.

Основная идея этого метода состоит в следующем: для доказательства не­выполнимости универсально квалифицируемой формулы, представленной в ви­де матрицы, необходимо доказать, что каждый вертикальный путь содержит контрарные литеры и для них существует подстановка, унифицирующая соот­ветствующие термы. Метод базируется на теореме П. Эндрюса. Пусть R —уни­версально квантифицированная формула, представленная в ННФ. Она не вы­полнима тогда и только тогда, когда некоторое расширение R имеет сцепку опровержения и, как следствие, ^-допустимую сцепку.

Возвращаясь к матрице (1), видим, что для F имеется р-допустимая сцепка ПР(У), Р(Ь)) для пути ~[Р\а), -\Р(у), ПР(а), "~\P{w), P{b), ~| Р{с)\ сцепка (Р(у), 100

"1 Р(х)) для пути Р(у), Р(а), Р(ш), Р(а), Р(г), ~| Р(х); сцепка (~\Р(а), Р(г)) для пути ~\Р(а), Р(а), P(w), Р(а), Р(г), ~\ Р(х) и т. д. —всего 32 пути. Отсюда очевидно, что F противоречива.

Поскольку число вертикальных путей через матрицу может быть значи­тельным, то особое внимание при реализации этого метода должно уделяться эффективности проверки этих путей. В [Andrews, 1981] предлагаются неко­торые пути решения этой проблемы. Так, нет необходимости рассматривать каждый вертикальный путь отдельно в полной мере. Как только найдена па­ра сцепленных литер на некоторой части пути, следует исключить из дальней­шего рассмотрения все расширения этой части.

Представление формул в виде матриц и методы доказательства теорем, основанные на таком представлении, были также рассмотрены в [Bibel, 1983; 1986].

Дедукция на семантических сетях

Одним из формализмов представления знаний являются семантические сети (см. § 1.3). Семантическая сеть в общем виде представляет собой информаци­онную модель предметной области, включая факты и общие закономерности (аксиомы, посылки). В вершинах сети помещаются объекты или- понятия, а дуги задают отношения между ними. С каждой семантической сетью сопо­ставлена совокупность дизъюнктов вида В1&В2&... &Вт-^-А\\/А2\/ ... \Mn (или

1 &1 V "I #2 V • • • V "1 Вт V А V • •. V Ai), где Bi — условия, Aj — заключения дизъюнкта.

Дизъюнкты, имеющие как условия, так и заключения, представляют собой общие законы (аксиомы), что соответствует интенсиональному представле­нию знаний. Дизъюнкты без условий — это факты, соответствующие экстенсио­нальному представлению. И, наконец, дизъюнкты без заключений — это отрица­ния фактов или цели, которые нужно доказать. Как обычно, используем про­цедуру опровержения при доказательстве теорем.

В семантической сети присутствуют два вида вершин: предикатные, соот­ветствующие предикатным буквам, входящим в дизъюнкты, и отвечающие дизъюнктам. Каждая дуга, идущая от дизъюнктной вершины в предикатную, взвешена атомом из этого дизъюнкта. Предикатные вершины связаны между собой дугами только через дизъюнктные вершины.

Для уменьшения перебора при поиске нужной информации, а также бо­лее быстрого и эффективного извлечения информации из сети введем опера* цию «раскраски» сети [Вагин и др., 1984]. Правило «раскраски* следующее: в дизъюнкте В-+А условие В будет «раскрашено» цветом Ц1 (на рис. 2.9, 2.10 соответствующие дуги изображены непрерывной линией), а заключение А — цветом Ц2 (соответствующие дуги — штриховой линией). Это правило распро­страняется на множество условий и заключений и на его частные случаи. Например, для дизъюнкта g: В\&Вг-+А\\/Аъ имеем дизъюнктную вершину g, четыре предикатные вершины В\, В₂, А_и А₂ и четыре дуги: две непрерывные, идущие от вершины g к В_х и В₂, и две штриховые, идущие от g к Ai и А₂.

Формально сеть задается четверкой вида L=<CG, P, Fi, F₂~>, где G — множество дизъюнктных вершин, Р — множество предикатных вершин, F_t — отображение G в Р на дугах, раскрашенных цветом Ц1, и F₂ — отображение С в Яна дугах, раскрашенных цветом Ц2.

Задача дедуктивного вывода формулируется следующим образом. Задана логико-лингвистическая модель в виде семантической сети, с которой сопо­ставлен набор дизъюнктов указанного типа, и на ее вход подается ситуация, представленная совокупностью фактов Аи А₂, .../А_г. Эта ситуация, накладывае­мая на семантическую сеть, представляет собой текущее состояние системы обработки знаний, отражающее динамику ее изменения. Кроме того, на вход модели подается запрос, также приведенный к виду дизъюнктов.

Решение задачи дедукции состоит в получении противоречий в семантиче­ской сети или пустой сети то аналогии с получением пустого дизъюнкта в прин-

101

Р(Ь)

г)

_I

ципе резолюции. Отметим, что процедура дедуктивного вывода на сети осно­вана на использовании многосортной логики предикатов первого порядка, что позволяет существенно ограничить область поиска необходимых утверждений, хотя сортность переменных может быть исключена введением соответствующих одноместных предикатов.

Существующие методы вывода на семантических сетях, использующие идею пересечения путей на сетях или наложения одного фрагмента сети на другой, имеют существенный недостаток. Основной недостаток, заключающийся в ог­раниченности дедуктивных возможностей вывода, связан с комбинаторным ро­стом числа наложений или пересечений и негибкостью этих методов при пере­ходе с одной предметной области на другую.

Рассмотрим три алгоритма дедукции на семантических сетях: для хорнов­ских дизъюнктов, связанный с трансформацией сети и нахождения пути на сети [Вагин и др., 1984].

Алгоритм дедукции на раскрашенных семантических сетях. Для предикат­ной вершины Р выбирается любая контрарная пара литер, которая затем ре-зольвируется. Если вершина содержит другие контрарные пары, то они рас­сматриваются как альтернативные и их выбор происходит только после неуда­чи с унификацией текущей контрарной пары. Если в вершину входят только дуги одного цвета (так называемые «чистые» дизъюнкты), то они не влияют на -процесс вывода пустой сети и удаляются из рассмотрения. Процегг продол­жается до тех пор, пока не будет выведена пустая сеть. Характерной чертой данного алгоритма является то, что в процессе вывода семантическая сеть не изменяется.

Алгоритм позволяет обрабатывать сети большой размерности и быстрее и эффективнее извлекать нужную информацию, чем другие методы вывода. Од­нако этот алгоритм неполон, т. е. не гарантирует в любых случаях получение пустой сети для исходного невыполнимого множества дизъюнктов. Алгоритм эффективен и полон для применения в таких системах обработки знаний, ко­торые описываются наборами хорновских дизъюнктов.

Алгоритм дедукции с использованием операторов удаления и расщепления вершин семантических сетей. Основан на преобразовании семантических сетей, для чего вводятся операторы трансформации сетей: оператор удаления верши­ны; оператор расщепления вершины.

Предикатная вершина считается свободной от мультидуг, если число дуг, выходящих из одной и той же какой-нибудь другой вершины и входящих в данную вершину, не больше единицы.

Правило удаления вершины следующее: если в сети имеется вершина Р, свободная от мультидуг, и этой вершиной связаны дизъюнкты gi, gt,*..,g_n, то после всевозможных резольвирований этих дизъюнктов по литере Р из сети эти дизъюнкты вместе с вершиной Р удаляются и добавляются новые дизъ­юнкты, полученные резольвированием g\, g2,—,gn. Вершина будет удалена из сети и в случае «чистого» дизъюнкта.

Проиллюстрируем оператор удаления вершины на примере рис. 2.2, задав следующую нотацию (см. набор дизъюнктов):

1) ~*С(а);

2) Р(у) -+Ца,у);

3) C(x)&H(y)&L(x,y)->

4. -/*(*);

5. ->//(&).

Здесь для фактов С(а), P(b), H(b) в условии дизъюнкта буква «и» (истина) для краткости опущена. Аналогично опущена буква «л» (ложь) в заключении дизъюнкта 3.

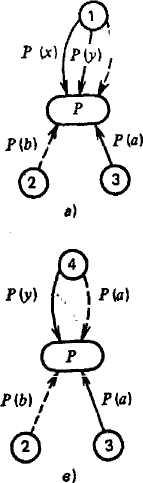
Раскрашенная сеть, соответствующая этому набору дизъюнктов, показана на рис. 2.9,а. Применив оператор удаления к вершине С, получим сеть, изобра-

102

Ряс. 2.9

женаую на рис. 2Д6, а к вершинам Н, L— противоречие в вершине Р или пустую сеть (рис. 2.9 а г).

Оператор расщепления вершины применяется при наличии в предикатной вершине мультидуг. Пусть имеется множество дизъюнктов 5«={Р\/Г, Ф}, где P\JT — дизъюнкт, в котором компонент дизъюнкта Г также содержит лите­ру Р, а Ф—любое подмножество дизъюнктов. После применения оператора расщепления множество 5 примет вид S' ={Р_г V Г, [Ф]^р^^р, Ф),

где [Ф]^Р*^|Р означает подстановку литеры Р_х вместо Р в дизъюнктах Ф, имеющих Р. Проиллюстрируем оператор расщепления на примере. Имеем следующий набор дизъюнктов:

2) 3)

103

Pi (X)

\p(fi)

Pib) /

Выделение литеры на семантической сети соответствует выделению соот­ветствующей вершины по дуге, которая взвешена этой литерой. Тогда путем на множестве дизъюнктов будем называть множество выделенных соответству­ющими литерами вершин на семантической сети. Для сетей этот алгоритм со­стоит в следующем: после выделения предикатных вершин получаем множест­во выделенных вершин, дизъюнкты которых или резольвируются, или нет. После резольвирования литеры вновь образованных дизъюнктов добавляются к выде­ленным вершинам, и процесс продолжается до получения противоречия в сети. Алгоритм полон.

Известно, что автоматическое доказательство теорем в силу вычислитель­ной сложности относится к труднорешаемым задачам [Rabin, 1974; Galil, 1975]. Поэтому возникает необходимость построения параллельных процедур дедуктивного вывода, в которых возможна независимая обработка порций зна­ний внутри одного обрабатывающего элемента, соединенного с другими ана­логичными элементами сетью сообщений. Такой возможностью обладает алго­ритм дедукции, связанный с трансформацией семантической сети. В этом ал­горитме имеется пять видов параллелизма [Вагин, 1986]:

1. Параллелизм при унификации, осуществляемый внутри одной вершины, свободной от мультидуг. Относящиеся к предикатной вершине дизъюнкты ре­ зольвируются по литере, принадлежащей этой вершине, т. е. осуществляется параллельная унификация аргументов литеры цвета 1 (2) с аргументами ли­ тер-кандидатов цвета 2 (I) и параллельная генерация новых дизъюнктов.

2. Параллельное удаление вершин, свободных от мультидуг, не имеющих общих дизъюнктов, т. е. параллельное применение оператора удаления вершин.

3. Параллельная стяжка мультидуг одного цвета (если это возможно) как внутри одной вершины, так и среди множества вершин.

4. Параллельное расщепление внутри одной вершины, имеющей несколько мультидуг.

5. Параллельное расщепление нескольких вершин, имеющих мультидуги.

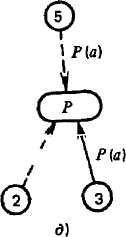
Рис. 2.10

Ему соответствует сеть, представленная на рис. 2Л0,а. Применяя оператор рас­ щепления, получаем сеть на рис. 2.10,6. Затем последовательно применяя one- ратор удаления к вершине Я, и оператор расщепления к вершине Р получа­ ем противоречивую сеть (рис. 2.10,5—д). ' "^^а Алгоритм вывода пустой сети с использованием операторов удаления и расщепления состоит в следующем: 1) если в сети имеются вершины к кото­ рым применим оператор удаления, то после его применения эти вершины уда­ ляются; 2) если в сети имеются вершины с мультидугами, то в результате применения оператора расщепления появляются вершины свободные от муль­ тидуг; затем снова применяем оператор удаления и т. д. до получения проти- воречия в сети.

Алгоритм выделения путей, Выделим из каждого дизъюнкта невыполнимо­го множества дизъюнктов 5 какую-нибудь литеру. Получим последовательность ли-ж!стее дизъюнктовS ^{последовательность лите}Р называется путем на мно-

Например, для 5== {Р(а) V Q (Ь), IQ(x), lP(x)\/C(d), ПОД} путем

ляп^^П^^{СЛеД0ВаГеЛЬН0СТЬ ЛИТер Р{п)}' 1 <?<*>• "1 ^РМ< "I ^СМ< Алгоритм выво­ да пустого дизъюнкта из невыполнимого множества дизъюнктов S состоит в следующем; 1) выделяем какой-нибудь путь П из исходного множества дизъ­ юнктов л; I) выводим всевозможные дизъюнкты на этом пути т е если на пути П имеются контрарные пары, то они резольвируются и их оставшихся частей дизъюнктов, к которым принадлежат эти пары, формируются новые дизъюнкты; 3) вновь сформированные дизъюнкты добавляются в S и в выб­ ранный путь П добавляем новые литеры из новых дизъюнктов- процесс про­ должается до получения пустого дизъюнкта. '

104