2. Инструментальные средства для разработки эс (аппаратные, программные, в т.Ч. Универсальные языки, символьные языки, языки представления знаний, оболочки).

Мощность инструм сред-ва: ИС тем более мощнее, чем меньше требует времени и трудозатрат на то чтобы создать с ее помощью готовую ЭС. Как можно большую по функциональности. Простота применения.

Эффективность ИС: более качественнее получается приложение, тем эффективней ИС.

Аппаратные средства: встроенные микропроцессоры либо автономная интеллектуальная машина.

Программные: (по уменьшению эффективности, но увеличению мощности): универс. Языки программирования, символьные яз. Программ (lisp, prolog), языки представл.знаний (emycin, frl), пустые системы и оболочки

Пустая система – готовая интелл. Система с пустой БЗ и рабочей памятью

Оболочка – набор инструментальных средств для построения систем

3. Робастные оценки параметров моделей.

Параметры модели (которые являются оценками параметров объекта), полученные на основе критерия наименьших квадратов, сильно реагируют на выбросы помех [6.9]. Аномальные отклонения в измерениях очень редки, но амплитуда их велика. Рассмотрим простейший пример. Считаем, что модель объекта равна одному параметру: 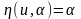. Из критерия наименьших квадратов (6.2.2) получаем, что есть среднее арифметическое измеренных значений выхода: 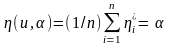. Считаем, что измерения выхода 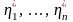упорядочены и одно измерение, например 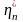, содержит очень большую помеху. Тогда основной вклад в выход модели вносит слагаемое 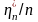и выброс существенно искажает модель.

Если в качестве критерия взять не квадратичный (6.1.2), а модульный критерий [6.9]

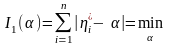, (6.5.1)

то параметром является оценка медианы: среднее по номеру значение в упорядоченной выборке . Аномальное измерение теперь не меняет параметра . Следовательно, критерий (6.5.1) обеспечивает получение более робастных (более крепких по отношению к выбросам измерений) параметров модели.

Кроме критерия (6.5.1) существуют другие, близкие к нему критерии [6.9]:

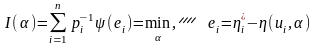, (6.5.2)

где 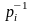– известные весовые коэффициенты. Примерами функций 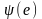являются:

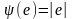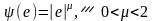(рис. 6.5.1 а); (рис. 6.5.1 б);

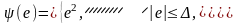(рис. 6.5.1 в).

1. 

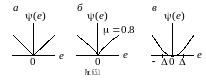
Для расчета параметров применим метод последовательной линеаризации. Вначале находим квадратичную аппроксимацию функционала 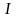[см. (6.5.2)] относительно траектории ( 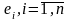), на которой он построен:

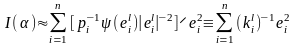. (6.5.3)

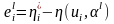Здесь – номер итерации; – невязка, 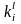– коэффициенты, которые для приведенных на рис. 6.5.1 случаев равны величинам:

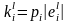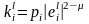а) , б) , в)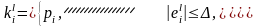 (6.5.4)

Теперь подставим в правую часть уравнения (6.5.3) (в квадратичный функционал) линейную аппроксимацию выхода модели

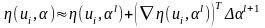(6.5.5)

и решаем обычную задачу наименьших квадратов

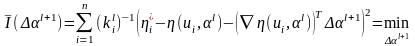(6.5.6)

относительно приращения параметров :

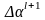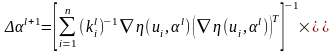
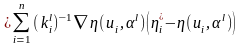. (6.5.7)

Следующее приближение параметров вычисляем по формуле (6.2.5):

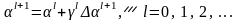. (6.5.8)

В отличие от обычного критерия наименьших квадратов при использовании неквадратичных критериев в алгоритме метода последовательной линеаризации меняются лишь весовые коэффициенты. Для измерений с выбросами автоматически понижаются весовые коэффициенты. За счет этого повышается робастность оценок.