12. Сети связи и структруные схемы динамических систем.

В динамической системе, как правило, протекают процессы

различной физической природы: механические, гидравлические,

электрические, тепловые и т. д. Основой для построения структурной

схемы такой системы служат физические законы. Они связывают

между собой физические величины внутри системы и внешние силы.

Основные уравнения динамической системы будем составлять с

использованием понятия "динамические звенья", изучаемого в ТАР.

На первоначальном этапе составления структурной схемы связи

между динамическими звеньями удобнее представлять в виде сети.

Подобно структурным схемам, сети связей физических величин или

просто сети связей используются для наглядного изображения

физических зависимостей динамических систем. Между структурной

схемой и сетью связей физических величин имеется прямое

соотношение: прямоугольник структурной схемы соответствует

ветви, а линия передачи сигнала - узлу сети [15].

Сравним структурную схему (рис.4.3) и сеть связей физических

величин (рис.4.4) одной и той же системы.

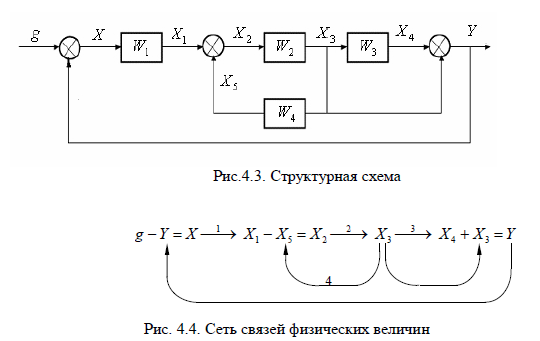
Правила составления сети связей физических величин:

1) номер ветви соответствует номеру передаточной функции

динамического звена;

2) ветвь, соединяющая одноименные величины, не имеет номера

(передаточная функция для такой ветви равна единице);

3) элементу сравнения на сети связей соответствует разность, а

сумматору - сумма двух величин, равная третьей величине

(результату);

4) результат вычитания или суммирования всегда записывают

справа от знака равенства.

Используя принцип декомпозиции, можно любую сколь угодно

сложную динамическую систему разделить на связанные между

собой элементарные звенья.

13. Математическая модель гидравлического демпфера.

Требуется построить структурную схему гидравлического

демпфера (амортизатора) с учетом массы подвижных частей. За

входную величину принята сила, а за выходную - перемещение

поршня (Рис.4.15).

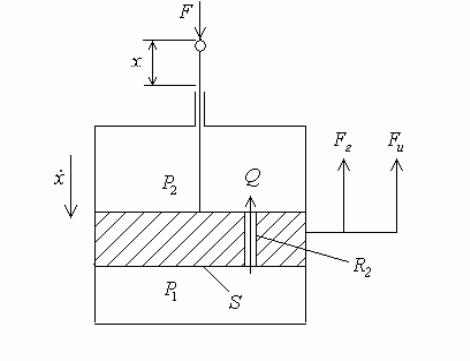где F - внешняя сила; г F - гидростатическая сила; и F - инерционная

сила; x - перемещение поршня; P1,P2 - давления в полостях

цилиндра; Q - расход жидкости через дроссель; S - площадь поршня;

Rг - гидравлическое сопротивление дросселя.

Здесь разность внешней силы F и внутренней гидростатической

силы Fг определяет инерционную силу Fи . Эта разность сил зависит

от разности давлений жидкости ∆P = P1 – P2 в нижней и в верхней

полостях цилиндра.

В свою очередь, инерционная сила Fи определяет ускорение

поршня x. Проинтегрировав ускорение x, получим скорость x , а

проинтегрировав скорость x , получим перемещение x . Скорость x определяет расход жидкости Q из нижней полости в верхнюю

полость, что при известном гидравлическом сопротивлении

дроссельного отверстия в поршне позволяет найти разность давлений

жидкости ∆P в нижней и в верхней полостях гидроцилиндра, а

следовательно, и гидростатическую силу Fг .

Сеть связей физических величин показывает рассмотренные

качественные зависимости физических величин (рис. 4.16).

Физические уравнения и соответствующие им передаточные

функции определяют количественные зависимости физических величин.

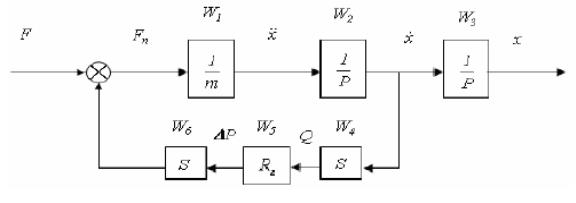
Структурная схема амортизатора

Структурная схема (рис.4.17) представляет собой

имитационную модель гидравлического амортизатора. Движение

этой модели легко описать с помощью системы линейных ДУ и

решить их с помощью ЭВМ.