5. Построение станочного зацепления

1. Откладываем от делительной окружности (с учетом знака) расчетное смещение 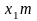и проводится делительная прямая исходного производящего контура реечного инструмента.

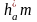1. На расстоянии влево и вправо от делительной прямой проводим прямые граничных точек, а на расстоянии 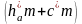- прямые вершин и впадин; станочно-начальную прямую проводим касательно к делительной окружности в точке 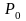(полюс станочного зацепления).

2. Проводим линию станочного зацепления 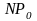через полюс станочного зацепления касательно к основной окружности в точке N. Эта линия образует с прямыми исходного производящего контура инструмента углы, равные .

3. Строим исходный производящий контур реечного инструмента. Закругленный участок профиля строим как сопряжение прямолинейной части контура с прямой вершин или с прямой впадин окружностью радиусом .

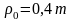4. Производим построение профиля зуба проектируемого колеса, касающегося профиля исходного производящего контура в точке К:

1. Для построения ряда последовательных положений профиля зуба исходного производящего контура проводим вспомогательную прямую ММ и прямолинейной части профиля инструмента 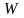и центр окружности закругленного участка профиля – точка .

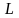1. Выбираем отрезок 10-15 мм и размечаем через одинаковые расстояния прямую ММ. Такие же по величине отрезки откладываем на станочно-начальной прямой и на дуге делительной окружности.

2. Из центра 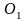колеса через отмеченные точки на делительной окружности проводим лучи до пересечения с окружностью вершин.

3. При перекрывании без скольжения станочно-начальной прямой по делительной окружности точка описывает укороченную эвольвенту, а точка - удлиненную.

4. Любое промежуточное положение точки или находим построением соответствующих треугольников.

5. К полученному ряду положений профиля зуба исходного контура инструмента проводим огибающую, которая определяет половину профиля зуба изготовляемого колеса.

6. Строим вторую половину профиля зуба.

7. Проводим качественное сравнение профиля, построенного по шаблону и профиля, построенного методом огибания . Совпадение удовлетворительное.

6. Выводы

1. Рассчитана эвольвентная зубчатая передача и выбран коэффициент смещения ;

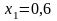1. Вычерчена эвольвентная зубчатая передача в масштабе ;

2. Проверен коэффициент торцевого перекрытия . Погрешность составила ;

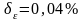3. Построено станочное зацепление для колеса и профиль зуба методом огибания;

Проведено качественное сравнение профиля, построенного по шаблону и профиля, построенного методом огибания. Совпадение удовлетворительное.

3. Синтез планетарного редуктора

1. Исходные данные:

Двухрядный планетарный редуктор со смешанным зацеплением

Передаточное отношение планетарного редуктора

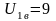
Число сателлитов k=3

Модуль всех колёс m=1 мм

Колёса нулевые и прямозубые

2. Постановка задачи:

1. Подобрать числа зубьев планетарного редуктора удовлетворяющее всем условиям многосателлитных планетарных редукторов

2. Построить схему планетарного редуктора в масштабе в двух проекциях

3. Построить диаграмму распределения угловых и линейных скоростей, чтобы проверить передаточное отношение редуктора графически

3. Основные условия проектирования многосателлитного планетарного редуктора:

1. Формула Виллиса:

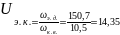
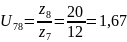
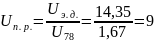
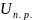=1+ =9; =8.

2. Условие соосности:

+ = .

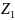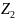3. Условие сборки:

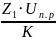⋅(1+P⋅K)=N, где N – целое число;

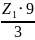⋅(1+3⋅P)=N; 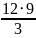⋅(1+3⋅P)=N 36+108⋅P=N.

4. Условие совместности:

sin > .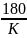

sin >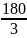

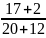
0,866>0,594

4. Подбор чисел зубьев планетарного редуктора

Анализируя условия сборки получаем, что число 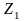кратно 3

Условия 1 и 2 решаем совместно методом неопределённых множителей

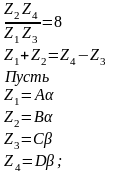
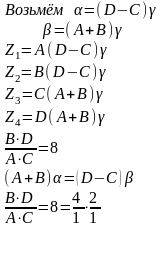
=1⋅(4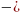 1)⋅γ=3⋅15=45;

=2⋅(4 1)⋅γ=6⋅15=90;

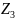=1⋅(1+2)⋅γ=3⋅15=45;

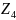=4⋅(1+2)⋅γ=12⋅15=180.

Проверка условий соосности:

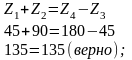
Проверка условия соседства:

sin > .

sin >

0,866>0,594; (верно).

5. Построение схемы планетарного редуктора и диаграммы распределения угловых и линейных скоростей

1. Радиусы колес планетарного редуктора:

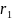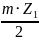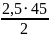= = =56,25 мм; 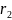= = =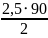112,5мм;

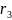= = =56,25 мм; 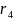= =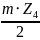 =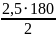225 мм.

1. Построение схемы планетарного редуктора в масштабе .

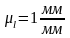2. Проверка передаточного отношения (графически из распределения линейных скоростей).

Для построения распределения линейных скоростей на схеме редуктора отмечаются характерные точки; центры колес и точки зацеплений, которые выносятся на вертикальную ось радиусов. Вычисляется

Задаём: .

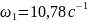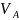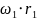= =10,78⋅0,05625=0,606 ,

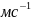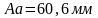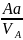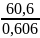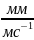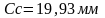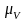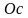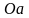Откладываем отрезок в масштабе = = =100 . Строим линию распределения скоростей блока сателлитов. Строим отрезок , выражающий в масштабе скорость точки С. Отрезок – линия распределения скоростей водила. Отрезок – линия распределения скоростей первого звена.

Проверка передаточного отношения (графически из распределения линейных скоростей).

;

;

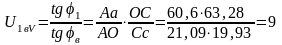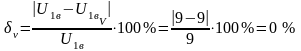3. Проверка передаточного отношения (графически из плана угловых скоростей).

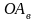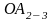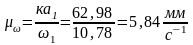Для построения плана угловых скоростей проводим горизонтальную линию угловых скоростей. Выбираем полюс на расстоянии 20мм от нее, проводим из него лучи параллельные линиям распределения скоростей до пересечения с осью. Отрезки , и выражают в масштабе угловые скорости соответствующих звеньев.

Проверка передаточного отношения (графически из плана угловых скоростей).

.

.
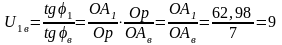
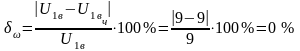