8. Гидростатическое давление и его свойства.

Гидростатика – раздел гидравлики, в котором рассматриваются законы равновесия жидкостей.

В гидростатике из поверхностных сил действуют только силы давления, причем действуют на внешнюю пов-ть жидкости по нормали к пов-ти внутрь объема, т.е. оказывают сжимающее воздействие .

Т.о. в подвижной жидкости возможен лишь один вид напряжения – напряжение сжатия , т.е. гидростатическое давление. В любой точке жидкости гидростатическое давление не зависит от ориентации площадки, на которую оно действует , т.е. от углов её наклона к координатным осям.

Док-во:

Р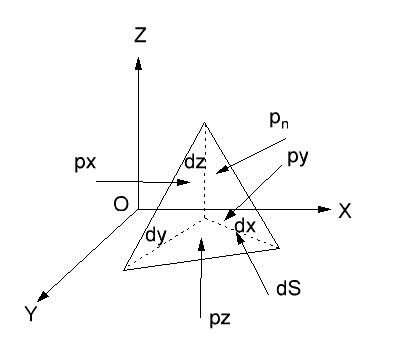 ассм. неподвижную жидкость, внутри её выделим объем, ограниченный тетрайдером со сторонами dx,dy,dz параллельными соответствующим осям.

Пусть внутри этого объема на жидкость действует ограниченая массовая сила с составляющими X,Y,Z.

Обозначим через px,py,pz гидростатические давления действующие на грани. Давление , действующее на грань dS , обозначим p_n .

Составим уравнение равновесия для выделенного объема согласно

1-му закону Ньютона.Запишем закон для оси Ох. На выделенный объем действуют 2 вида сил : массовая сила и сила от гидростатического давления. Проекция сил на ось Ох:

Массовая сила , действующая в направлении Ох:

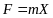
Уравнение равновесия тетрайдера имеет вид:

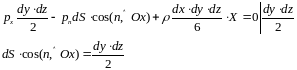
Разделим обе части на ;

При стягивании тетрайдера в точку имеем:

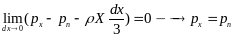
Аналогично доказывается для осей Oy и Oz получим:

Т.к. выраженные пар-ры тетрайдера были взяты произвольно ,то при стягивании его в точку давление в этой точке по всем направлениям будет одинаково.

9. Основное уравнение гидростатики. Закон Паскаля

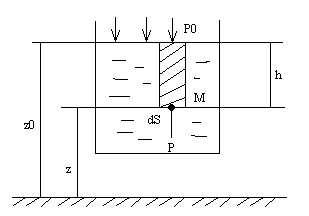
Рассмотрим случай, когда на жидкость действует только одна сила – сила тяжести. Имеется сосуд с жидкостью, на свободную поверхность которой действует сила от давления Р₀ . Определим гидростатическое давление в произвольно взятой точке М на глубине h. Около точки М выделим горизонтальную элементарную площадку dS. Построим вертикальный цилиндр высотой h и площадью основания dS. По 1-му з-ну Ньютона рассмотрим условие равновесия этого цилиндра:

ρ·g·dS·h+P₀·dS-P·dS=0 / dS

P=P₀+ρ·g·h – основное уравнение гидростатики, позволяет определить давление в любой точке покоящейся жидкости.

З-н Паскаля: давление, приложенное к внешней пов-ти жидкости передается всем точкам этой жидкости и по всем направлениям одинаково.

Отложим от базовой плоскости координату z – коорд.точки М,z₀ – координата свободной поверхности.В основном ур-нии гидростатики запишем: h=z₀-z; P=P₀+ρ·g(z₀-z); z+P/ρg=z₀+P₀/ρg.

Т.к точка М была взята произвольно, то для всего объема неподвижной жидкости можно записать: z+P/ρg=const, где z – геометрическая высота(напор),м;P/ρg –пьезометрическая высота; z+P/ρg – гидростатическая высота. Вывод:для всего объема покоящейся жидкости гидростатический напор – величина постоянная.

10. Дифференциальные уравнения равновесия жидкости

Допустим, мы имеем произвольные массовые силы. Обозначим единичные массовые силы по соотв.направлениям след.образом:X,Y,Z. Запишем уравнения Эйлера:

Домножим ур-ния на dx,dy,dz и сложим их:

Xdx+Ydy+Zdz-1/ρ( .

Выражение , стоящее в скобках представляет собой полный дифференциал давления: dp=ρ(Xdx+Ydy+Zdz). Данное выражение определяет приращение давления при приращении координат dx,dy,dz. Рассм.частный случай,когда действует только сила тяжести: Y=X=0; Z=-g; dp=-ρgdz. Проинтегрируем обе части:p=-ρgz+c. Константу с находим по координате свободной пов-ти:

p₀==-ρgz₀+c; c=p₀+ρgz₀;

p+ρgz= p₀+ρgz₀;/ разделим на ρg

z+p/ρg=z₀+p₀/ρg.

Таким образом з-н Паскаля явл-ся частным случаем ДУ равновесия жидкостей.