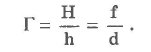61. Юнг поставил такой опыт: свет от двух щелей был направлен на экран, в результате чего на экране получалась не меняющаяся во времени картина, состоящая из чередующихся тёмных и светлых полос. Но ведь если свет - это поток частиц (корпускул), то на экране должны были появиться две светлые точки! Юнг объяснил появление этих полос интерференцией света.

Интерференция света поражает многочисленные явления, наблюдаемые в жизни, например радужные пленки мыльных пузырей или тонких пленок нефти на воде. Окраска возникает в результате усиливающей интерференции света, отраженного двумя поверхностями тонкой пленки.

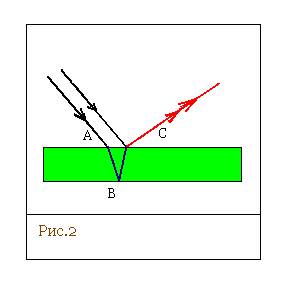
Рис. 2. Интерференция света

62.Рассмотрим тонкую пленку (Рис.3). Часть падающего света отражается в точке А от верхней поверхности, а часть проходит во внутрь пленки и отражается в точке В от нижней поверхности. Он проходит в пленке расстояние АВС. Если расстояние АВС равно длине волны или целому значению длин волн, то обе волны (отраженная в т.А и т.В) интерферирую, усилят друг друга, и мы увидим свет. Если же путь АВС равен λ/2, 3λ/2 и т.д. то обе волны окажутся в противофазе, и интерферируя, погасят друг друга. Под длинной волны имеем в виду длину волны в пленке ( λ_n= λ/n).

Рис. 3. Интерференция света в тонких пленках

Если на тонкую пленку падает белый свет, путь АВС будет равен λ (или mλ, где m — целое число) при данном угле зрения только для определенной длины волны. Соответствующая окраска будет очень яркой. Для света, падающего под иным углом, путь АВС будет короче или длиннее, и и усиливающая интерференция происходит для другого цвета. Таким образом, при наличии протяженного (неточечного) источника белого цвета мы увидим яркие разноцветные полосы, расположенный друг за другом. Неоднородность пленки по толщине также изменяет путь  АВС и, следовательно, влияет на окраску наиболее ярко отраженного цвета.

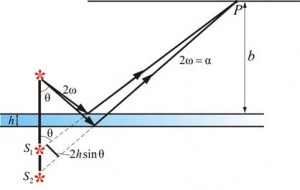
63. Дифра́кция Френе́ля — дифракционная картина, которая наблюдается на небольшом расстоянии от препятствия, по условиям, когда основной вклад в интерференционную картину дают границы экрана.

На рисунке схематично изображён (слева) непрозрачный экран с круглым отверстием (апертура), слева от которого расположен источник света. Изображение фиксируется на другом экране - справа. Вследствие дифракции свет, проходящий через отверстие, расходится, поэтому область, которая была затемнена по законам геометрической оптики, будет частично освещённой. В области, которая при прямолинейном распространении света была бы освещённой, наблюдаются колебания интенсивности освещения в виде концентрических колец.

Дифракционная картина для дифракции Френеля зависит от расстояния между экранами и от расположения источников света. Её можно рассчитать, считая, что каждая точка на границе апертуры излучает сферическую волну по принципу Гюйгенса. В точке наблюдения (занимаемое вторым экраном) волны или усиливают друг друга, или гасятся в зависимости от разности хода.

Дифракция – огибание светом препятствия, проникновение света в область геометрической тени.

Принцип Гюйгенса — Френеля: Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Дифракция Френеля:

На рисунке изображён непрозрачный экран с круглым отверстием, на некотором расстоянии от которого расположен источник света. Изображение фиксируется на другом экране справа. Вследствие дифракции свет, проходящий через отверстие, расходится. Поэтому область, которая была затенена по законам геометрической оптики, будет частично освещённой. В области, которая при прямолинейном распространении света была бы освещённой, наблюдаются колебания интенсивности освещения в виде концентрических колец.

64. Дифракция Фраунгофера — случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Расстояние должно быть таким, чтобы можно было пренебречь в выражении для разности фаз членами порядка , что сильно упрощает теоретическое рассмотрение явления. Здесь — расстояние от отверстия или преграды до плоскости наблюдения, — длина волны излучения, а — радиальная координата рассматриваемой точки в плоскости наблюдения в полярной системе координат. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля , при этом приходящие в точку волны являются практически плоскими. При наблюдении данного вида дифракции изображение объекта не искажается и меняет только размер и положение в пространстве. В противоположность этому, при дифракции Френеля изображение меняет также свою форму и существенно искажается.

Дифракционные явления Фраунгофера имеют большое практическое значение, лежат в основе принципа действия многих спектральных приборов, в частности, дифракционных решёток. В последнем случае для наблюдения светового поля «в бесконечности» используются линзы или вогнутые дифракционные решетки (соответственно, экран ставится в фокальной плоскости).

65. 5. Поляризация света. Поляризованный свет. Плоскополяризованный свет, свет, поляризованный по кругу и эллипсу. Получение поляризованного света. Двойное лучепреломление в кристаллах. Призма Николя Поляризация света при отражении Угол Брюстера, закон Брюстера. Оптически активные среды Вращение плоскости поляризации.

 Поляризованный свет. Плоскополяризованный свет, свет, поляризованный по кругу и эллипсу.

В электромагнитной волне, распространяющейся в свободном пространстве, векторы напряженности электрического (E) и магнитного (Н) полей взаимно перпендикулярны, изменяются синхронно (см. рис.1) и их величины связаны соотношением:

        где ₀ и ₀ ^- соответственно электрическая и магнитная постоянные.

Поэтому в световой электромагнитной волне достаточно знать поведение .лишь одного из векторов. Обычно для этой цели выбирают вектор E.

В естественном свете имеются колебания вектора E волны, совершающиеся в различных направлениях, перпендикулярных к лучу. Свет, в котором направления колебаний вектора E упорядочены каким либо образом, называется поляризованным.

Поляризация света - это физическая характеристика оптического излучения, описывающая неэквивалентность различных направлений колебаний вектора E волны в плоскости, перпендикулярной световому лучу.

Волна называется линейно поляризованной (или иначе плоско поляризованной), если в процессе распространения волны вектор E лежит в одной плоскости, параллельной направлению распространения волны.

Плоскостью поляризации называется плоскость, проходящая через направление колебаний электрического вектора E линейно поляризованной световой волны и направление распространения этой волны (плоскость PР1, см. рис.2а). Плоско поляризованную волну излучает, например, отдельный атом.

Волна называется поляризованной по кругу (или волной с циркулярной поляризацией), если конец вектора E описывает в плоскости, перпендикулярной направлению распространения волны, окружность.

При вращении конца вектора E по часовой стрелке говорят о правой круговой поляризации волны, а при вращении против часовой стрелки, соответственно, о левой круговой поляризации. Если конец вектора E описывает в пространстве эллипс, то тогда говорят о эллиптически поляризованной волне.

 Получение поляризованного света. Прохождение света через поляризатор. Закон Малюса.

 Для экспериментального анализа поляризации света используют поляризаторы. Поэтому кратко рассмотрим их принцип действия. Поляризатор представляет собой устройство для получения линейно поляризованного света. Действие поляризаторов основано на том, что они пропускают световые колебания лишь в определенной плоскости, которая проходит через ось поляризатора.

  Линейно поляризованная волна, падающая на поляризатор, может быть разложена на две взаимно перпендикулярные составляющие: Е|| - параллельную оси поляризатора, и Е - перпендикулярную этой оси

Составляющая E, перпендикулярная плоскости РР, поглотиться поляризатором, а составляющая Е|| пройдет через поляризатор. .Поэтому амплитуда волны, прошедшей через поляризатор, будет равна Е = Еосоs , (10) где - угол между направлением колебаний вектора напряженности электрического поля падающей на поляризатор волны и плоскостью поляризатора.

Интенсивность световой волны пропорциональна квадрату амплитуды напряженности, поэтому интенсивность света прошедшего через поляризатор будет равна: = ocos² , (11)

где o - интенсивность, падающего на поляризатор линейно поляризованного света. Соотношение (11) носит название закона Малюса и формулируется следующим образом:

интенсивность света, прошедшего через поляризатор пропорциональна интенсивности линейно поляризованного света, падающего на поляризатор и квадрату косинуса угла между плоскостью поляризации падающего света и плоскостью поляризатора.

При падении на поляризатор естественного света, как следует из формулы (7), интенсивность любых двух взаимно перпендикулярных составляющих всегда будут равны друг другу. Т.е. при любом положении поляризатора = (12)

Следовательно, интенсивность естественного света, прошедшего через поляризатор, всегда будет равна = ₀/2, (13)

где o - интенсивность естественного света, падающего на поляризатор.

66. Построение изображения в линзе

 Тонкая линза характеризуется главным образом расположение своих фокусов. То есть при построении изображений в тонкой линзе, нет необходимости рассматривать ход лучей внутри линзы, а следовательно и рисовать на чертеже сферические поверхности линзы и т.д.

Для обозначения собирающей тонкой линзы на чертежах принят следующий рисунок.

картинка

Для обозначения рассеивающей тонкой линзы на чертежах принят следующий рисунок.

картинка

Тонкая линза может дать изображение любого предмета. Так как все лучи, которые вышли из одной точки и прошли сквозь линзу, соберутся также в одной точке. Таким образом, мы можем получить изображение любой точки предмета, а значит и всего предмета в целом.

Построение изображение в линзе

При построении изображений различных предметов в тонкой собирающей линзе, для которой заданы её фокус и оптический центр, мы будем использовать так называемые «удобные» лучи.

Нам уже известно, что луч, проходящий через оптический центр тонкой линзы, не будет преломляться. Вообще он должен немного сместиться, но для тонкой линзы этим смещение можно пренебрегать.

Лучи, которые направлены параллельно главной оптической оси, после преломления в линзе будут проходить через её фокус. Следовательно, если луч попал в линзу, пройдя через её фокус, то после преломления в линзе он будет направлен параллельно главной оптической оси.

Рассмотрим следующий рисунок.

картинка

На нем представлены лучи, с помощью которых строится изображение предмета АВ в тонкой собирающей линзе. Направим из точки А луч параллельный главной оптической оси. Как уже известно, после преломления он пройдет через фокус линзы.

Далее построим луч АО. Так как он проходит через оптический центр линзы, он не будет преломляться. Эти два луча пересекутся в точке А1. Это и будет изображение точки А в собирающей тонкой линзе. 

В принципе, мы могли выбрать другой луч, например, тот, что проходит через фокус и построить его. Это луч AD. Так как он проходит через фокус линзы, то после преломления он будет направлен параллельно главной оптической оси. Он пересекается с другими лучами в точке А1.  

Однако, не стоит думать, что изображение строится тремя этими лучами. На самом деле, оно получается с помощью всего огромного множества различных лучей которые проходят через точку А и попадая на линзу собираются в точке А1. Просто нет смысла отмечать все эти лучи на чертеже.

67. Формула тонкой линзы связывает d (расстояние от предмета до оптического центра линзы), f (расстояние от оптического центра до изображения) с фокусным расстоянием F (рис. 101). Автор: Написал: Amro Дата: 22-Окт-2006

Формула тонкой линзы

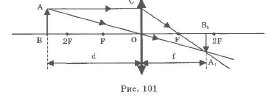
Формула тонкой линзы связывает d (расстояние от предмета до оптического центра линзы), f (расстояние от оптического центра до изображения) с фокусным расстоянием F (рис. 101).

Треугольник АВО подобен треугольнику OB₁A₁. Из подобия следует, что

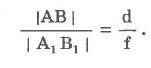
Треугольник OCF подобен треугольнику FB₁A₁. Из подобия следует, что

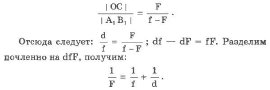
Это и есть формула тонкой линзы.

Расстояния F, d и f от линзы до действительных точек берутся со знаком плюс, расстояния от линзы до мнимых точек - со знаком минус.

Отношение размера изображения Н к линейному размеру предмета h называют линейным увеличением линзы Г.