10.7. Методика расчета толщины изоляции

Принятая конструкция теплоизоляции должна иметь толщину не выше установленных норм и обеспечивать: заданные пределы изменения температуры теплоносителя на всех участках тепловой сети; допустимую температуру на поверхности изоляции; непревышение нормативных теплопотерь.

Рассмотрим условие, при котором материал, используемый для изоляции трубы, будет уменьшать тепловые потери.

Пусть цилиндрическая труба покрыта однослойной изоляцией. При постоянных a₁, a₂, d₁, d₂, l₁, l₂, t₁ и t₂ рассмотрим, как будет изменяться полное термическое сопротивление при изменении толщины изоляции.

В уравнении общего термического сопротивления двухслойной цилиндрической стенки

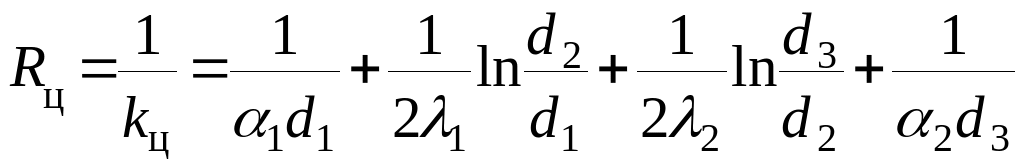(10.39)

при увеличении внешнего диаметра изоляции d₃ увеличивается сопротивление слоя изоляции (член ), но одновременно уменьшаетея сопротивление теплоотдачи на наружной поверхности изоляции (член ).

Беря первую производную от правой части уравнения по d₃ и приравнивая ее нулю, получаем

d(R_ц)/d(d₃) = 1/(2l₂d₃)-1/(?₂d₃²)=0 (10.40)

Тогда критический диаметр изоляции, отвечающий экстремальной точке кривой R=f(d₃), определится формулой

d_кр=d_из=2l_2из/a₂ (10.41)

Из уравнения следует, что критический диаметр d_кр изоляции не зависит от размеров трубопровода. Он будет тем меньше, чем меньше теплопроводность изоляции и чем больше коэффициент теплоотдачи a₂ от наружной поверхности изоляции к окружающей среде.

Вторая производная от R_ц больше нуля. Следовательно, критический диаметр соответствует минимуму теплового сопротивления и максимуму теплового потока (рис. 10.12).

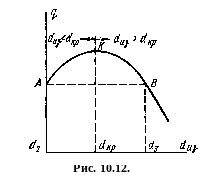
Анализ уравнения (10.41) показывает, что если наружный диаметр изоляции d_из увеличивается, но остается меньше d_кр, то тепловые потери возрастают и будут больше теплопотерь голого трубопровода (кривая АК). При равенстве d_из=d_кр получаются максимальные теплопотери в окружающую среду (точка К). При дальнейшем увеличении наружного диаметра изоляции d_из>d_кр теплопотери будут меньше, чем при d_из=d_кр (кривая ВК).

Только при d_из=d_кр тепловые потери вновь станут такими же, как и для неизолированного трубопровода.

Значит, для эффективной работы изоляции необходимо, чтобы критический диаметр был меньше внешнего диаметра оголенного трубопровода, т. е. чтобы d_кр<d₂ (рис. 10.12). Таким образом, для того чтобы изоляция вызвала уменьшение теплопотерь цилиндрической стенки по сравнению с голым трубопроводом, при данном наружном диаметре трубы d₂ и заданном коэффициенте теплоотдачи a₂ необходимо, чтобы

a_из<a₂d₂/2

Например, для изоляции трубопровода диаметром d₂=30 мм имеется шлаковая вата, теплопроводность которой a_из=0,1 Вт/(м·К), коэффициент теплоотдачи l₂=4,0Вт/(м₂·К) Целесообразно ли применять в данном случае в качестве изоляции шлаковую вату?

Критический диаметр изоляции

d_кр=2l_из/a₂=2·0,1/4·0,05 м=50 мм

Так как d_кр>d₂, шлаковую вату в рассматриваемом случае применять нецелесообразно.

Для нашей задачи l_из должна быть меньше

l_из<4·0,03/2=0,06 Вт/(м·К)

т.е. для изоляции нужно брать другой изоляционный материал, у которого l<0,06Вт/(м·К). После выбора материала изоляции расчитывают толщину изоляционного слоя по вышеизложенной методике.

В общем случае толщина изоляции может быть определена по нормативным теплопотерям. Для чего, приняв допустимые удельные теплопотери, по формуле (10.11) определяют потребную величину полного термического сопротивления изоляции R. Задавшись ориентировочным диаметром изоляции d_и (в пределах рекомендуемых толщин слоя), по формуле (10.3) определяют термическое сопротивление изоляции R_и.

Потребная толщина слоя изоляции найдется из равенства (10.7), приведенного к виду

(10.42)

где d_н- наружный диаметр изолируемой трубы; R_и- термическое сопротивление слоя изоляции, R_и=R - R_н.

При выборе толщины изоляции теплопроводов следует учитывать требования со стороны производственного процесса, включая охрану труда, и нормативные тепловые потери, установленные для данного производства с помощью технико-экономических расчетов.

К производственным требованиям относится, например, обеспечение заданной температуры в паропроводе по его длине при транспортировке перегретого пара отдельным абонентам.

Влияет также на выбор толщины изоляции необходимость поддержания по условиям техники безопасности температуры поверхности изоляции теплопроводов, проложенных в рабочих помещениях или в проходных каналах, не выше 40-50° С.

По указанным выше производственным требованиям определяется минимально необходимая толщина изоляции, но она может быть принята большей на основании технико-экономического расчета,

Увеличение толщины изоляции ведет, с одной стороны, к экономии средств путем снижения тепловых потерь, с другой стороны - к росту капиталовложений на сооружение изоляции. Оптимальная толщина изоляции соответствует минимальным годовым приведенным затратам.

На результат технико-экономического расчета могут влиять косвенные затраты, зависящие от толщины изоляции. К ним относятся: капитальные затраты на выработку теплоты, теряющейся в окружающую среду; затраты на опорные конструкции теплопроводов; затраты на земляные работы и строительные сооружения при подземных прокладках и др. Однако влияние этих затрат обычно незначительно.

Пример 1. Определить толщину изоляции паропровода с наружным диаметром 0,273 м, проложенным на эстакаде. Среднегодовая температура окружающей среды 0°С, температура пара 200°С. Тепловая изоляция выполняется из минераловатных прошивных матов с обкладками. ,

Решение. Для средней температуры изоляции 100°C теплопроводность минераловатной изоляции составляет 0,064 Вт/м·°С. Нормативные теплопотери для паропровода составляют 162 Вт/м. Полное термическое сопротивление изолированного паропровода, рассчитанное по формуле (10.11), равно R=(200-0)/162=1,23 м·°С/Вт.

По нормам предельная толщина изоляции составляет 0,l8 м, поэтому d=0,273+2·0,18=0,633 м. Коэффициент теплоотдачи от поверхности изоляции при скорости ветра 10 м/с по формуле (10.5) равен 33,7 Вт/м²·°С.

Проверяем пригодность минеральной ваты для изоляции в данных условиях

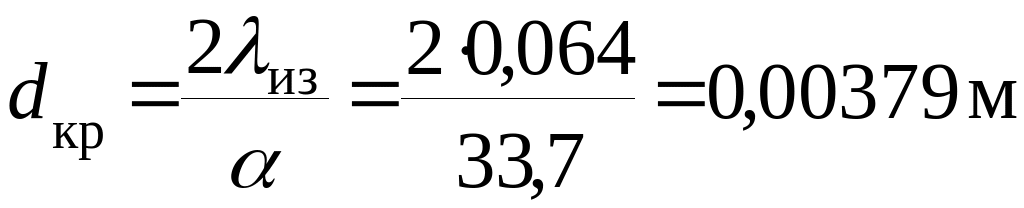
т.к. d_кр=0,00379<d_тр=0,273, изоляция пригодна для рассматриваемого трубопровода.

Термическое сопротивление теплоотдаче от поверхности изоляции по формуле (10.3) равно:

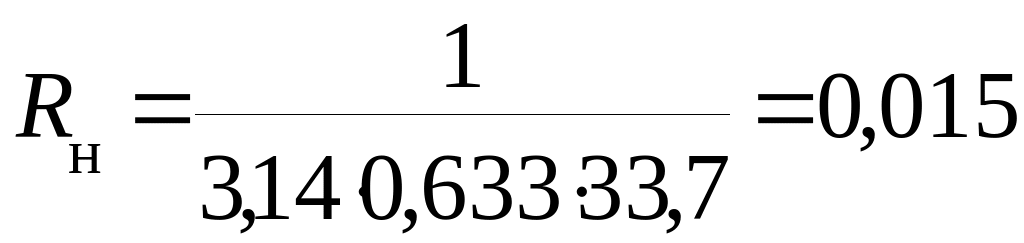м·°С/Вт

По формуле (10.39) найдем

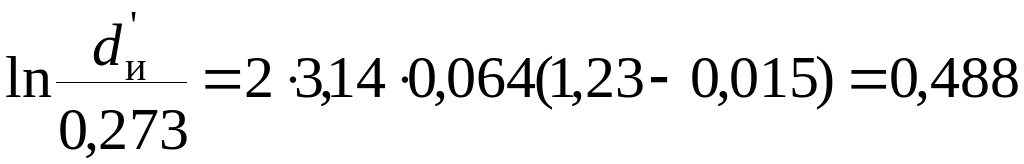
откуда получаем d_и'=0,444 м.

Примем в первом приближении d_и''=0,444 м, при этом получим

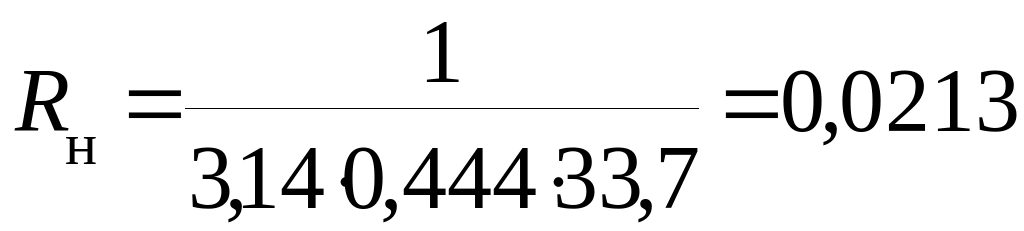м·°С/Вт

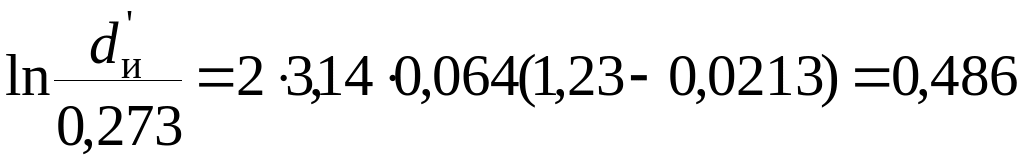
и соответственно d_и@0,444 м, которое очень близко со значением первого приближения d"_и.

Температура на поверхности изоляции при d_и =0,444, найденная по формуле (10.13)

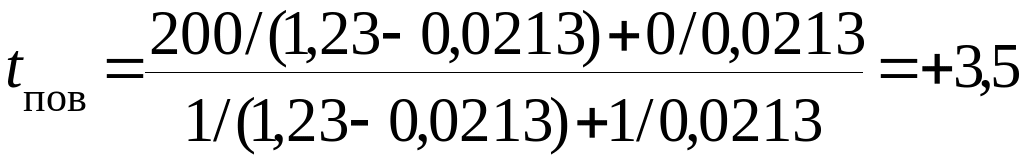°С

не превышает нормы.

Пример 2. Определить удельные потери тепла подающего и обратного трубопроводов диаметров d₁=d₂=0,273 м, проложенных бесканально (pиc. 10.8) в маловлажных суглинистых грунтах на глубине h=l,5 м с расстоянием между осями труб по типовому проекту b=0,65 м. Температура в подающем трубопроводе t₁=150°С, в обратном ?₂=70°C. Толщина изоляции на подающем трубопроводе—0,14 м, на обратном—0,05 м. Коэффициент теплопроводности изоляции l_n=0,12 Вт/м·°С. Температура грунта на глубине заложения труб t_o=+5°С, для этих условий коэффициент теплопроводности грунта l_г=1,75 Вт/м·°С.

Решение. При

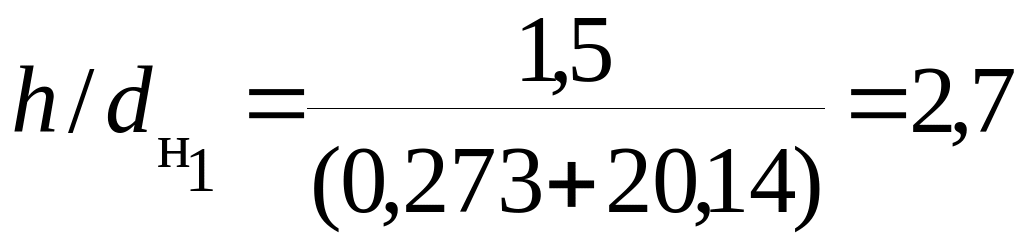
термическое сопротивление грунта определяют по формуле (10.9).

Условное термическое сопротивление по формуле (10.15) равно:

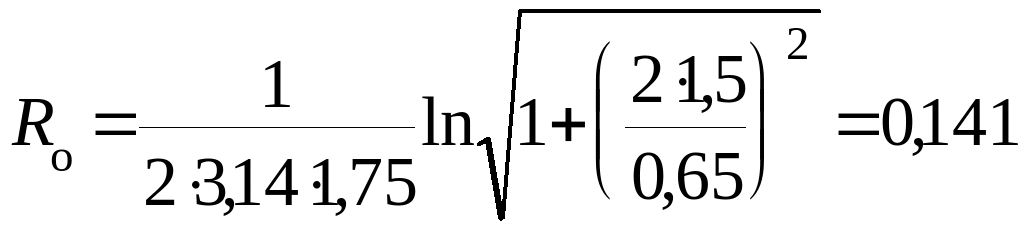м·°С/Вт.

Полные термические сопротивления подающего и обратного трубопроводов находят по формулам (10.7), (10.9) и (10.14):

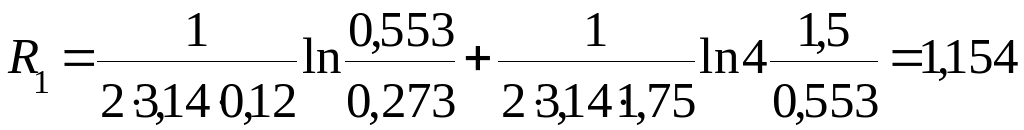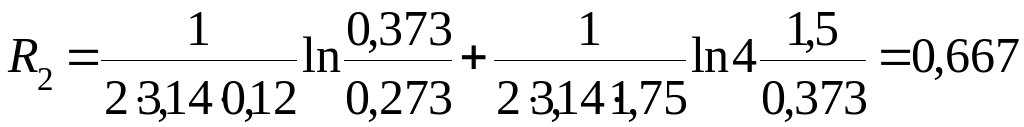м·°С

м·°С

Удельные тепловые потери подающего и обратного трубопроводов по формулам (10.16) и (10.17) равны:

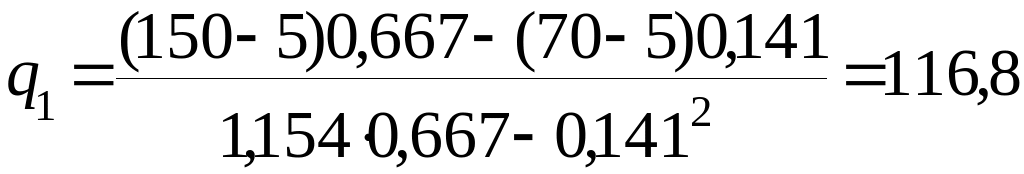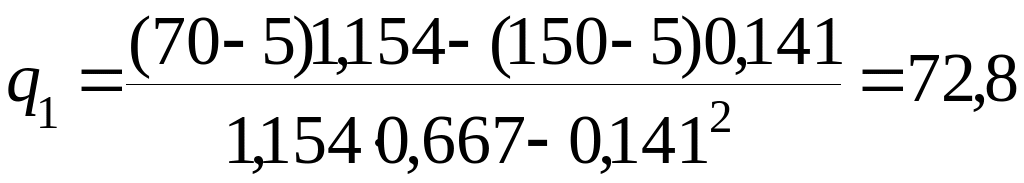Вт/м

Вт/м

Температура грунта в точке А (рис. 10.8) при х=0,8 м и y=0,9 м по формуле (10.19) равна:

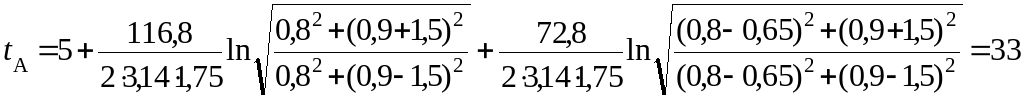°С