
- •Недостатки:
- •Протокол:
- •Идея электронной цифровой подписи
- •Односторонняя функция (one-way function)
- •Свойства:
- •Односторонняя функция с секретом (one-waytrap-doorfunction)
- •Свойства:
- •Режим простой замены (ecb)
- •Недостатки:
- •Области использования:
- •Режим простой замены (ecb)
- •Свойства гаммирования
- •Сравнительная характеристика поточного и блочного шифрования
- •Поточный криптоалгоритм
- •Режим гаммирования с обратной связью (cfb)
- •Режим контроля целостности (mac)
- •Достоинства:
- •Решение:
- •Стохастический код Осмоловского
- •4Операции:
- •Рюкзачная криптосистема (KnapsackCryptosystem).
- •Подсистема управления:
- •Подсистема обнаружения вирусной активности:
- •Сигнатурный анализ
- •Эвристический анализатор Задача:
Задачи обеспечения безопасности информации (ОБИ), решаемые стохастическими методами
Обеспечение секретности (конфиденциальности) информации
Обеспечение аутентичности информации
Обеспечение аутентичности субъектов информационного взаимодействия
Защита прав собственника информации
Обеспечение юридической значимости электронных документов
Обеспечение устойчивости к разрушающим программным воздействиям (РПВ)
Обеспечение неотслеживаемости информации
Функции генераторов псевдослучайных чисел (ГПСЧ) в системах ОБИ
Генератор гамма-шифра при шифровании методом гаммирования
Генератор ключей и паролей пользователей
Формирование случайных запросов при аутентификации удаленных абонентов по принципу вопрос-ответ
Затемняющий множитель в слепой ЭЦП
Формирование контрольных кодов целостности (наложение на защищаемые данные ПСП).
Функции хеш-генераторов в системах ОБИ
Сжатие информации, т.е. преобразование документа в документ фиксированной длинны
Может пароли (ХЭШ образ, а потом его шифруй, если захочешь)
формирование серийного номера купюры в циф. Деньгах
формирование документа в слепой ЭЦП (ГПСП вырабатывает прекурсор, а затем получается его хеш-образ - это и есть документ)
Требования к качественной хеш-функции
ХЭШ образ должен зависеть от всех входных значений
Минимальное изменение документа должно приводить к существенным изменениям на выходе
Необратимость, т.е. по ХЭШ образу нельзя найти исходный документ
Задача нахождения коллизий, вычислительно неразрешима
На выходе образ фиксированной длинны
Требования к качественному шифру
Минимальные изменения на входе должны приводить к существенным изменениям информации на выходе
Минимальное изменение ключа при неизменной входной информации должно приводить к существенному изменению информации на выходе.
Отсутствие закономерностей в последовательности ключевой информации
На выходе не должно быть закономерностей.
Требования к качественному ГПСЧ
ГПСЧ должен быть не предсказуемым, за это отвечает функция EAB
важно чтобы у ГПСЧ был большой период формируемой последовательности
Нет зависимости
При каждом шаге существенное отличие от предыдущего значения
Модель криптосистемы с секретным ключом
E – процесс зашифрования
– процесс зашифрования
D– процесс расшифрования.
Недостатки:
необходимость надёжного канала связи (КС) для обмена ключами;
отсутствие юридической значимости пересылаемых документов
Блок замены (S-блок)
Д ля
реализации блока надо иметь таблицу
замен. Если исходные данные 4-х разрядные,
то в памяти надо будет хранить таблицу
размером 16×4=64 байта, а если исходные
данные 8-и разрядные, то 256×8=2048 байт
ля
реализации блока надо иметь таблицу
замен. Если исходные данные 4-х разрядные,
то в памяти надо будет хранить таблицу
размером 16×4=64 байта, а если исходные
данные 8-и разрядные, то 256×8=2048 байт
|
P1 |
C2 |
|
0000 |
0101 |
|
0001 |
1100 |
|
… |
… |
|
1111 |
0100 |
Шифр RC4
С четчик
перебирает значения и через 256 тактов
таблица полностью изменится. В начале
работы в регистре и счетчике записаны
произвольные значения.
четчик
перебирает значения и через 256 тактов
таблица полностью изменится. В начале
работы в регистре и счетчике записаны
произвольные значения.
Генерация состоит из 5 шагов:
Счетчик +1:

Содержимое счетчика рассматривается как индекс таблицы. Содержимое регистра суммируется с содержимым S(Q1):



 3
3
Модель криптосистемы с открытым ключом. Криптосистема RSA
Идея предложена Диффи и Хеллманом в 1978 г.

![]() –секретный
(security) ключ абонентаB– ключ расшифрования.
–секретный
(security) ключ абонентаB– ключ расшифрования.
![]() –открытый (public)
ключ абонентаB– ключ
зашифрования
–открытый (public)
ключ абонентаB– ключ
зашифрования
Справочник открытых ключей, хранит все открытые ключи всех абонентов
Проблема:
Подлинность открытых ключей, взятых из справочника. Нет гарантий, что не подменили справочник открытых ключей
Справочник открытых ключей

![]() и
и
![]() формирует противник.
формирует противник.
Криптосистема с открытым ключом RSA
Построение криптосистемы RSA. В 1978г. числа, используемые в этом алгоритме имели 50 десятичных разрядов.p, q– простые большие различные числа. Для примера возьмемp=3 иq=11.


нужно найти
 взаимно простое к
взаимно простое к (не имеют общих делителей, кроме 1).
(не имеют общих делителей, кроме 1).
находим число
 такое что
такое что

А лгоритм
шифрования
лгоритм
шифрования
Расшифровывание
![]()
Стойкость
этого шифра равносильна разложению
числа
![]() на простые сомножители
на простые сомножители![]()
![]() –ключ зашифрования
(открытый ключ)
–ключ зашифрования
(открытый ключ)
![]() –ключ расшифрования
(секретный ключ)
–ключ расшифрования
(секретный ключ)
Протокол электронной подписи RSA

абонент А: h(m)
А подписывает хеш-образ документа

абонент А формирует сообщение для отправки абоненту B

 .
Bнаходитh(m’)
.
Bнаходитh(m’)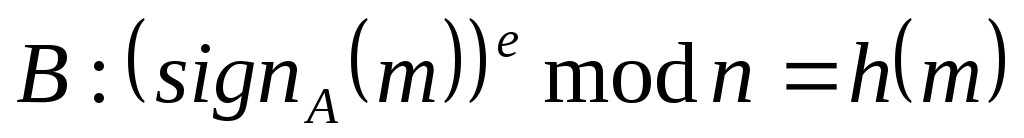

Протокол «Слепой» ЭЦП RSA
 (это и есть документ)
– получает хеш-образ
(это и есть документ)
– получает хеш-образА запускает ГПСП и получает случайное число R(blinkingfactor) – секретное число


 ,
где m – случайное
число (прекурсор), после хеширование
превращается в документ
,
где m – случайное
число (прекурсор), после хеширование
превращается в документ
П
 ротокол
выработки общего секретного ключа
ротокол
выработки общего секретного ключа
![]() –главный кандидат
на звание односторонней. Эта функция
– модульное возведение в степень.
–главный кандидат
на звание односторонней. Эта функция
– модульное возведение в степень.
Обратная задача– дискретное логарифмирование (вычислительно неразрешима).
![]() –открытые
параметры, известны всем.
–открытые
параметры, известны всем.
![]() –очень большое
простое число (несколько десятков
десятичных знаков).
–очень большое
простое число (несколько десятков
десятичных знаков).
![]() –обычное большое
число в первом приближении. Это примитивный
элемент конечного поля.
–обычное большое
число в первом приближении. Это примитивный
элемент конечного поля.
Протокол:
протокол стохастический (используется генерация псевдо-случайных чисел). Абонент Авырабатывает большое случайное число (секретный ключxA) затем формирует и передает абоненту B сообщение
 Абонент
Bзапускает свой ГПСП и вырабатывает
случайное секретное число (xB),
формирует и передает абоненту А сообщение
Абонент
Bзапускает свой ГПСП и вырабатывает
случайное секретное число (xB),
формирует и передает абоненту А сообщение
 .
.
Примеры:
15 mod7 = 1
17 mod5 = 2
21 mod20 = 1
Абонент Авыполняет операцию –
 .
Это число абонент А объявляет общим
секретном ключом.Абонент B
.
Это число абонент А объявляет общим
секретном ключом.Абонент B
Протокол электронной цифровой подписи (ЭЦП)
