11. Ознака подільності на 3. На 3 діляться ті й тільки ті натуральні числа, сума цифр яких ділиться на 3.
Ознака подільності на 9. На 9 діляться ті й тільки ті натуральні числа, сума цифр яких ділиться на 9.
12. Дільник- число на яке ми ділимо.
Число а назив. дільником числа в, якщо існує таке число с,що в=а∙с
За кілкістю дільників множина цілих невідємних чисел ділиться на 4 класи підмножин.
НСД(а,в)- це найбільший з усіх існуючих спільних дільників а і в. щоб знайти НСД:
числа а і в розкладають на прості множики.
вибирають лише спільні множники з найменшим показником та перемножають їх.
13. Кратне – число яке ми ділимо.
НСК(а,в)- найменше спільне кратне а і в – найменше з усіх можливих чисел,що діляться на а і в одночасно.
щоб знайти НСК (а,в)
числа а і в розкл. на прості множники.
спільні множники вибирають з найбільшим показником, потім вибирають всі можл. множники, що входять хоч в один з розпадів так перемножають їх.
Властивості НСД і НСК(а і в )
1.Якщо найбільший спільний дільник = 1, то а і в- взаємнопрості.
2. Якщо а:в, то НСД буде= в, а НСК (а,в)=а.
3. НСК(а,в)=а∙в
НСД(а,в)
14. Обчислення найбільшого спільного дільника і найменшого спільного кратного за канонічним розкладом чисел
Теорема. НСД а,b є найменшим спільним кратним усіх спільних дільників чисел а і b. Нехай треба знайти НСД і НСК двох чисел 360 і 525. За основною теоремою арифметики ці числа можна подати однозначно у канонічному вигляді. Будь-яке натуральне число, більше 1, може бути розкладене в добуток простих співмножників. Цей розклад є єдиним, якщо не враховувати порядок слідування співмножників.
360 = 23?32?5; 525 = 3?52?7. У розклад на прості множники НСД цих чисел повинні ввійти всі спільні прості множники, причому кожний з них треба взяти з найменшим показником, з яким він входить в канонічні розклади даних чисел. Отже, НСД 360, 525 = 3?5 = 15. У розклад на прості множники НСК 360, 525 повинні ввійти всі прості множники, які входять принаймні в один розклад, причому кожний з них треба взяти з найбільшим показником. НСК 360, 525 = 23 ? 32 ? 52 ? 7 = 12600. За аналогічним правилом знаходять НСК і НСД будь-яких двох чисел. Теорема. НСДа, b ? НСКа, b = а ? b. Наслідок. Якщо НСДа, b = 1, то НСКа, b = аb. Таким чином, НСК двох чисел дорівнює добутку цих чисел тоді і тільки тоді, коли ці числа взаємно прості. Щоб знайти НСД натуральних чисел за їхнім канонічним розкладом, треба спочатку розкласти ці числа на прості множники. Для великих чисел це складна задача. З часів Евкліда ІІІ ст. н. е. відомий більш ефективний спосіб знаходження НСД, який оснований на діленні з остачею і називається алгоритмом Евкліда.
15.Алгоритм Евкліда обчислює найбільший спільний дільник (НСД) двох натуральних чисел a та b. Найбільший спільний дільник g — це найбільше натуральне число яке ділить як a так і b без залишку. Найбільший спільний дільник також записують як НСД(a, b) або, простіше, (a, b) хоча останнє позначення використовують і для інших математичних понять, таких як координати дво-вимірних векторів.
Якщо НСД(a, b) = 1, тоді a та b називають взаємно простими. Ця властивість не залежить від того, чи прості числа a та b. Наприклад, ні 6 ні 35 не прості, оскільки їх можна розкласти на добутки 6 = 2 × 3 та 35 = 5 × 7. Однак, 6 та 35 взаємно прості. Жодне натуральне число окрім 1 не ділить водночас 6 та 35, оскільки у них нема спільних дільників.
Алгоритм Евкліда один з найдавніших алгоритмів, що досі використовують. Він описаний в Началах Евкліда (приблизно 300 до н. е.), а саме, в книгах VII та X. В сьомій книзі алгоритм описано для цілих чисел, а в десятій — для довжин відрізків. Можна сказати, що алгоритм описано для дійсних чисел. Однак, довжина, площа та об'єм, що їх вимірюють нині в дійсних числах, вимірюють у різних одиницях та не існує універсальної природньої одиниці для вимірювання довжини, площі або об'єму. Також поняття дійсних цисел в ті часи було ще не відоме. Другий алгоритм геометричний. НСД двох довжин a та b відповідає довжині найдовшого відрізку g, яким можна виміряти a та b без залишку; іншими словами, довжини відрізків a та b дорівнюють добуткові довжини g на ціле число.
Можливо, алгоритм було відкрито не Евклідом, а він лише використав результати, отримані попередниками в Началах. Математик та історик Ван дер Варден вважає, що книгу VII написано на основі підручника з теорії чисел авторства одного з математиків школи Піфагора. Ймовірно, алгоритм був відомий ще Евдоксу Кіндському (приблизно 375 до н. е.). Можливо, навіть, алгоритм був відомий ще до Евдокса, судячи з використання поняття грец. ἀνθυφαίρεσις (антифарезис) в роботах Евкліда та Арістотеля.
Нові можливості застосування алгоритму Евкліда було знайдено в XIX столітті. В 1829 році Чарльз Штурм застосував алгоритм Евкліда в методі Штурма для пошуку дійсних коренів поліномів у заданому інтервалі.
У випадку невеликих чисел, можна використати послідовне ділення у стовпчик. Наприклад, нам потрібно знайти НСД (2700, 1520):
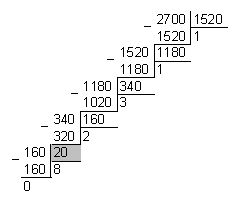
Отже, НСД (2700, 1520) = 20.