Практическая работа № 5
Задания:
Вычислить приближенное значение определенного интеграла
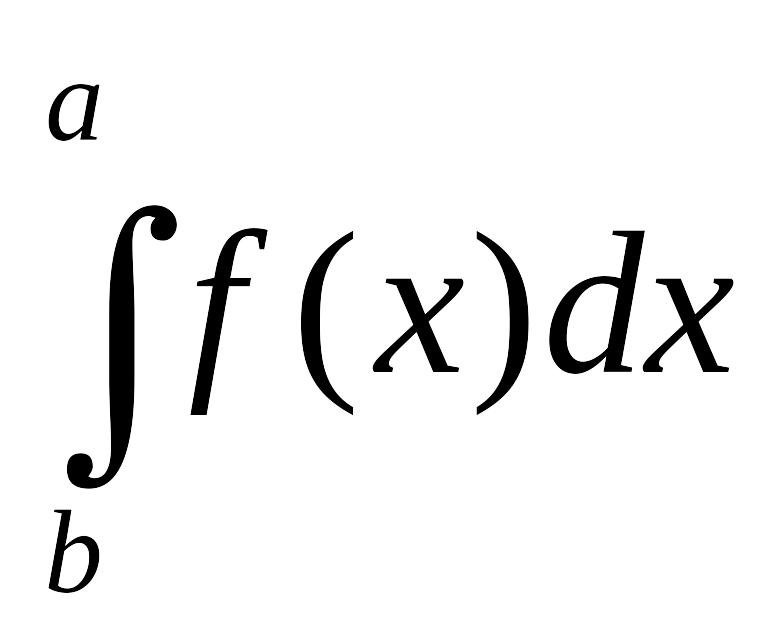от заданной функции (см. таблицу 1) по
обобщенной формуле трапеций, если число
частичных отрезков задано: n
=
10 (составить алгоритм). Оценить погрешность
вычислений, пользуясь формулой
остаточного члена.Вычислить этот же интеграл по формуле средних прямоугольников. Оценить погрешность вычислений. Сравнить точность полученных по разным формулам результатов.
Вычислить определенный интеграл от заданной функции (см. таблицу 2) с точностью до = 10-4 по общей формуле Симпсона (составить алгоритм с использованием формулы двойного пересчета).
Вычислить интеграл от заданной функции (см. таблицу 3) по формуле Гаусса, применяя для оценки точности двойной пересчет при
.
Данные к заданию 1-2 (таблица 1):
№ |
f(x) |
a |
b |
1 |
|
0 |
3 |
2 |
|
4 |
6 |
3 |
|
0 |
1 |
4 |
|
-3 |
-1 |
5 |
|
2 |
3 |
6 |
|
-2 |
0 |
7 |
|
-1 |
0 |
8 |
|
1 |
4 |
9 |
|
3 |
5 |
10 |
|
0 |
1 |
11 |
|
1 |
3 |
12 |
|
0 |
1 |
Данные к заданию 3 (таблица 2):
№ |
f(x) |
a |
b |
1 |
|
0.8 |
1.8 |
2 |
|
0.8 |
1.8 |
3 |
|
0.6 |
1.6 |
4 |
|
3 |
4 |
5 |
|
1 |
2 |
6 |
|
2 |
3 |
7 |
|
3 |
4 |
8 |
|
1.3 |
2 |
9 |
|
0 |
1 |
10 |
|
2 |
3 |
11 |
|
0.8 |
2.8 |
12 |
|
2 |
4 |
Данные к заданию 4 (таблица 3):
№ |
f(x) |
a |
b |
1 |
|
-0.5 |
1.3 |
2 |
|
2 |
3.2 |
3 |
|
0.5 |
1.6 |
4 |
|
2.2 |
3.4 |
5 |
|
1.2 |
2 |
6 |
|
2.2 |
3.8 |
7 |
|
0.2 |
2.4 |
8 |
|
1 |
2.6 |
9 |
|
0.8 |
1.6 |
10 |
|
-0.4 |
1.6 |
11 |
|
-0.8 |
1.4 |
12 |
|
2.6 |
3.4 |
Контрольные вопросы:
Понятие определенного интеграла.
В чем заключается принцип двойного пересчета?
Геометрический смысл квадратурных формул?
Оценка точности квадратурных формул?
Формулы трапеции и прямоугольников.
Формула Симпсона.