12_)Продольные и поперечные деформации. Закон Гука

Иметь представление о продольных и поперечных деформация! и их связи.

Знать закон Гука, зависимости и формулы для расчета на­пряжений и перемещений.

Уметь проводить расчеты на прочность и жесткость ста­тически определимых брусьев при растяжении и сжатии.

Деформации при растяжении и сжатии

Рассмотрим деформацию бруса под действием продольной силы F (рис. 21.1).

Рис. 21.1

Начальные размеры бруса: lo – начальная длина, ао — начальная ширина. Брус удлиняется на величину Δl; Δl - абсолютное удлинение. При растя­жении поперечные размеры уменьшают­ся, Δа — абсолютное сужение; Δl > 0; Δа < 0. При сжатии выполняется соотноше­ние Δl < 0; Δа > 0. В сопротивлении материалов приня­то рассчи-

тывать деформации в относи­тельных единицах:

; ε - относительное удлинение;

; ε' – относительное сужение.

Между продольной и поперечной деформациями существует за­висимость

ε' = με,

где μ — коэффициент поперечной деформации, или коэффициент Пуассона, -характеристика пластичности материала.

Ускорение характеризует не только изменение величины скорости, но и изменение ее направления. Очевидно, что быстрота изменения направления вектора скорости, при прочих равных условиях, зависит от степени искривленности траектории. Для количественной оценки этой искривленности вводится понятие кривизны.

13)Предельные и допустимые напряжения

Предельное напряжение-напряжение при котором в материале возникает опасное состояние

Для пластичных материалов напряжение считается предел текучести, так как возникает пластичная деформация не исчезают после снятия нагрузки

Сигма пред = сигма т

Для хрупких материалов пласт.деформации отсутствует разрушение возникает по хрупкому типу

Предел напряжение=предел текучести

Для пластично хрупких материалов предельное напряжение является напряжение соот. Макс. Деформации

Сигма пред=сигма прочности

Допускаемое напряжение-максимальное напряжение при котором материал должен нормально работать .допускаемое напряжение

Сигма доп=сигма пред\коэфффициент запаса прочтности

14) Расчеты на прочность при растяжении и сжатии

3 вида на прочность расчеты

проектировочный

В проектировочном размеры определяют размер поперечного сечения

А=N\G

Подбор материала

Сигма пред больше или равно N[s]\A

Проверочный расчет при при нем известны материал нагрузка и размеры деталей

Сигма=N\A меньше или равно [сигма]

Определение нагрузочной способности

Определение мах нагрузки

[N]=[сигма]-A

15. Напряжения в любой точке поперечного сечения. Максимальные напряжения при кручении

Напряжение в любой точке поперечного сечения

Рис. 27.2

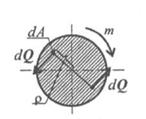
Рассмотрим поперечное сечение круглого бруса. Под действием внешнего момента в каждой точке поперечного сечения возникают силы упругости dQ (рис. 27.2). dQ = τdA, где τ — касательное напряжение; dA — элемен­тарная площадка. В силу симметрии сечения силы dQ образуют пары.

Элементарный момент силы dQ относительно центра круга

dm = pdQ,

где р — расстояние от точки до центра круга.

Суммарный момент сил упругости получаем сложением (интегрированием) элементарных моментов:

.

После преобразования получим формулу для определения напря­жений в точке поперечного сечения: Эвольвентное зубчатое колесо и его параметры. Толщина зуба колеса по окружности произвольного радиуса. Понятие о исходном, исходном производящем и производящем контурах. Станочное зацепление. Основные размеры зубчатого колеса. Виды зубчатых колес. Подрезание и заострение колеса. Понятие о области существования зубчатого колеса. Эвольвентная цилиндрическая зубчатая передача и ее параметры. Основные уравнения эвольвентного зацепления.

, где .

При ρ = 0 τк = 0; касательное напряжение при кручении пропорционально расстоянию от точки до центра сечения. Полученный интеграл Jp называется полярным моментом инерции сечения. Jр является геометрической характеристикой сечения при кручении. Она характеризует сопротивление сечения скручиванию.

2)Вращающийся стержень, работающий на кручение называют валом. Стержень, используемый как упругий элемент, который работает на скручивание, называется торсионом. Касательные напряжения , возникающие в условиях кручения, определяются по формуле:

,

где r — расстояние от оси кручения.

Очевидно, что касательные напряжения достигают наибольшего значения на поверхности вала при и при максимальном крутящем моменте , то есть

,

где W_p — полярный момент сопротивления.

Это даёт возможность записать условие прочности при кручении в таком виде:

17. Напишите формулы для определения момента инерции и момента сопротивления для прямоугольника. Что характеризуют эти величины. Укажите единицы измерения этих величин

,?????????????????????????????