
- •4.Дать понятие :пара сил, плечо пары, момент силы относительно точки.
- •Характеристики пластичности материала
- •1.15.Статический момент площади сечения,...Рассмотрим произвольное сечение.
- •Центробежный момент инерции
- •Полярный момент инерции сечения
- •Первая, вторая, четвертая аксиома статики
- •3)Определение равнодействующей системы сил аналитическим способом
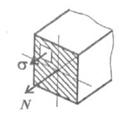
- •18)Сформулируйте закон парности касательных напряжений
- •19) Напишите формулу для расчета нормальных напряжений при изгибе
- •4) Условия равновесия плоской системы сходящихся сил в аналитической форме
- •8) Порядок построения многоугольника сил
- •9) Неподвижный шарнир, защемление или «заделка»
- •10) Классификация нагрузок и элементов конструкции
- •12_)Продольные и поперечные деформации. Закон Гука
- •13)Предельные и допустимые напряжения
- •14) Расчеты на прочность при растяжении и сжатии
- •15. Напряжения в любой точке поперечного сечения. Максимальные напряжения при кручении
- •16. Виды расчетов на прочность при кручении. Расчет на жесткость
- •18.Перечислите факторы, влияющие на сопротивление усталости
- •19. Что называется пределом выносливости. Как строится кривая усталости
- •20. Какие гипотезы выполняются при кручении
- •21. Перечислите характеристики циклов, покажите на графиках среднее напряжение и амплитуду цикла. Что характеризует коэффициент асимметрии цикла
- •22. Дать понятие: главные оси, главные моменты инерции, осевые моменты инерции круга и кольца
- •23) Запишите условие прочности на сдвиг и смятие. Чем отличается расчет на прочность при сдвиге односрезной заклепки от двухсрезной
- •24) Виды диаграмм растяжения, их значения
4) Условия равновесия плоской системы сходящихся сил в аналитической форме
Равнодействующая равна 0
Плоская система сход. Сил нахдоится в равновесии если алгебраическая сумма проекций всех сил системы на любую ось равна 0
5)Определение реакций опор и моментов защемления
???????????????????????????????????????????????????????????
6)Шарнирно-подвижная и шарнирно-неподвижная опора
Шарнир допускает поворот вокруг точки закрепления
Различают 2 вида
Подвижный
Стержень закрепленный может поворачивать вокруг шарнира а точка крепления может перемещаться вдоль направляющей
Реакция перпендикулярна опорной поверхности
Неподвижный
Стержень может свободно поворачивайть вокруг оси шарнира
Реакция проходит через ось шарнира
7) Теорема Вариньона, его значение
Решение вопроса упрощает теорема Вариньона, согласно которой момент равнодействующей системы сил относительно какого-либо центра равен геометрической сумме моментов составляющих систему сил относительно того же центра.
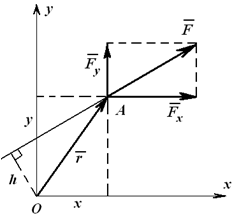
8) Порядок построения многоугольника сил
Определить возможное направление реакции связей
Вычертить многоугольник сил системы начиная с известных сил
Измерить полученые векторы сил и определить их величину
Для уточнения решения рекомендуется опеределить величину векторов с помощью геометр. Зависимости
Если плоская система сход.сил находится в равновесии то многоугольник замкнется.
9) Неподвижный шарнир, защемление или «заделка»
Неподвижный
Стержень может свободно поворачивайть вокруг оси шарнира
Реакция проходит через ось шарнира
Защемление или заделка-любые перемещения точки крепления невозможны
Под действием величины сил в опоре возникает реактивная сила и реактивный моменмт
Которая препятствует повороту
Реактивная сила представляется в виде двух частей R=Rx+Ry
10) Классификация нагрузок и элементов конструкции
Статические нагрузки
Не меняются со временем или меняются очень медленно при действии стат.нагрузок проводится расчет на прочность
Повторно переменные нагрузки
Многократно меняют значения и знак
Действие таких нагрузок вызывает усталость металла
Динамические нагрузки
Меняют своё значение в коротком промежутке времени
Вызывают большие ускорения и силы энерции могут вести к внезапному разрушении конструкции
Нагрузки 2 видов
Сосредоточенные и поверхностные
11)Напряжения при растяжении и сжатии
При растяжении и сжатии в сечении действует только нормальное напряжение.
Напряжения в поперечных сечениях могут рассматриваться как силы, приходящиеся на единицу площади.
Таким образом, направление и знак напряжения в сечении совпадают с направлением и знаком силы в сечении (рис. 20.3).
Исходя из гипотезы плоских сечений, можно предположить, что напряжения при растяжении и сжатии в пределах каждого сечения не меняются. Поэтому напряжение можно рассчитать по формуле
![]() ,
,
где Nz — продольная сила в сечении; А — площадь поперечного сечения.
Величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна, площади поперечного сечения.
Нормальные напряжения действуют при растяжении от сечения (рис. 20.4а), а при сжатии к сечению (рис. 20.46).
Размерность (единица измерения) напряжений — Н/м2 (Па), од- жако это слишком малая единица, и практически напряжения рассчитывают в Н/мм2 (МПа): 1 МПа = 106 Па = 1 Н/мм2.
При определении напряжений брус разбивают на участки нагружений, в пределах которых продольные силы не изменяются, ж учитывают места изменений площади поперечных сечений. |
Рис. 20.4 |

