Первая, вторая, четвертая аксиома статики
Первая аксиома:под действием уравновеш. системы сил абсолютно твердое тело и матер.точка находятся в равновесии или движутся равномернои прямолин.(закон инерции.2 аксиома:две силы равные по модулю направл.по одной прямой в разные стороны,уровновешиваются.4 аксиома:равнодейств.двухсил приложенных в одной точку,приложена в этой же точке и явл-тся диагональю парал-ма,построенного на этих силах как на сторонах.
2) Условие равновесия плоской системы сходящихся сил:при равновесии системы сил равнодейств.должна быть равна нулю,при геометрич.построении конец последнего вектора должен совпасть с нач.первого.Если плоская система сход.сил находится находится в равновесии многоуг.сил этой системы должен быть замкнут.Если в системе три силы,образ-тся.треуг сил.
3)Определение равнодействующей системы сил аналитическим способом
Величина
равнод.равна векторной(геом.сумме
векторов системы сил).1)Определяют
равнод.геом.способом.2)Выбирают систему
координат.3)Определяют проекции всех
заданных векторов на эти оси.4)складывают
проекции всех векторов на оси х и у.
4)Теорема Пуансо о параллельном переносе сил:силу можно перенести параллельно линии ее действия,при этом нужно добавить пару сил с моментом,равным произведению модуля силы на расстояние,на которое перенесена сила.
5) Условие равновесия произвольной плоской системы сил:для того,чтобы твердое тело под длействием произвольной плоской системы сил находилось в равновесии,необходимо и достаточно,чтобы его алгебр.сумма проекций всех сил системы на любую ось равнялось нулю и алгебр.сумма моментов всех сил системы относительно любой точки в плоскости действия сил равнялось нулю.
6)Виды нагрузок и разновидности опор:по способу приложения нагрузки делятся на сосредоточенные и распределенные.Если реально передача нагрузки происходит на пренебрежимо малой площадке(в точке),нагрузку наз.сосредоточенной.Часто нагрузка распределена по знач.площадке или линии(давление воды на плотину,давление снега на крышу),тогда нагрузку считают распред.Балка-конструкт.деталь в виде прямого бруса,закреплен.на опорах и изгиб.приложен.к ней силами. Шарнирно-неподвижная опора препятствует любому поступательному перемещению балки, но дает возможность последней поворачиваться вокруг оси шарнира. Шарнирно-подвижная опора – нижняя часть – поставлена на катки (рисунок 2.28,а), поэтому такая опора не препятствует небольшому перемещению балки в направлении, параллельном опорной поверхности. Жесткая заделка препятствует любому поступательному движению балки и повороту последней в плоскости действия сил.
7)Запишите формулы для расчета главного вектора пространственной системы сходящихся сил, пространственной системы произвольно расположенных сил,пространственной системы сил
главного
вектора пространственной системы
сходящихся сил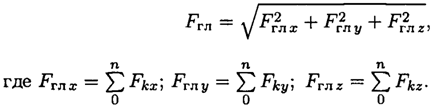
пространственной
системы сил
8)
Какую
из форм уравнений равновесия целесообразно
использовать при определении реакци в
заделке
9) Балка на двух шарнирных опорах
В отличие от консольных балок, при расчете балок на двух шарнирных опорах необходимо сначала определить опорные реакции из уравнений статики, так как и в левую, и в правую отсеченные части для любого сечения, расположенного между опорами, попадает соответствующая реакция.
Для
плоской системы число уравнений статики
в общем случае равно трем. Если балка
загружена только вертикальными
нагрузками, то горизонтальная реакция
шарнирно-неподвижной опоры равна нулю,
и одно из уравнений равновесия (
Fix =
0) обращается в тождество. Таким образом,
для определения реакций в опорах
шарнирной балки используются два
уравнения статики:
МА = 0,
МВ = 0.
10) Формы элементов конструкции:Брус-это любое тело,у которого длина значительно больше других размеров.В зависимости от форм продольной оси и поперечных сечений различают неск-ко видов брусьев:прямой брус постоянного поперечногосечения,прямой ступенчатый брус,криволин.брус.Пластина-любое тело,у которого толщина значит.меньше других размеров.Массив-тело,у которого три размера одного порядка.
11) Растяжение и сжатие. Внутренние силовые факторы, напряжения
Расстяжением или сжатием наз.вид нагружения,при котором в поперечном сечении бруса возникает только один внутр.силов.фактор-продольная сила.Продольные силы меняются по длине бруса.При расчетах после определ.величин продольных сил по сечениям строится график-эпюра.Если прод.сила направлена от сечения,то брус растянут,растяжение считают полож.деф-цией.Если продольная сила направлена к сечению,то брус сжат.Сжатие считают отриц.деф-цией.
12)Гипотезы плоских сечений:заключ.в том,что поперечное сечение бруса,плоское и перпендик.продольной оси,после деф-ции остается плоским и перпендик.продольной оси.След-но,продольные внутренние волокна удлиняются одинаково,а внутренние силы упругости распредел.по сечению равномерно.
13) Виды диаграмм растяжения.Различн.материалы по-разному ведут себя под нагрузкой,хар-тер деформации и разрушения зависит оттипа материала.принято делить материалы по типу их диаграмм растяжения на три группы.К 1 группе относят пластичные материалы,эти материалы на диагр.растяж имеют площадку текучести.Ко 2 группе отн.хрупкие материалы,эти материалы мало деф-тся,разруш.по хрупкому типу,на диагр.нет площадки текучести.К 3 группе относят материалы,не имеющие пощадки текучести,но знач-но деф-ся под нагрузкой,их наз.пластично-хрупкими.
14) Сдвиг и смятие, их значения. Какие внутренние силовые факторы возникают при сдвиге и смятии.
Сдвигом наз.нагружение,при котором в поперечном сечении бруса возникает только один внутр.силов.фактор-поперечная сила. Смятие – деформация, обусловленная местным сжатием материала в соприкасающихся деталях по площадкам передачи давления.
15) Кручение. Угол сдвига. Деформации при кручении. Эпюры крутящих моментов
Круче́ние —
один из видов деформации тела,это
нагружение при котором в поперечном
сечении бруса возникает только один
внутр.силовой фактор,крутящий момент.На
кручение работают пружины растяжения-сжатия и валы.Кручение
круглого бруса происходит при нагружении
его парами сил с моментами в плоскостях,
перпендикулярных продольной оси. При
этом образующие бруса искривляются и
разворачиваются на угол γ,назыв.углом
сдвига(угол поворота образующей).
При
кручении возникает напряжённое состояние,
называемое «чистый сдвиг»
При
сдвиге на боковой поверхности элемента
1234 возникают касательные напряжения,
равные по величине, элемент деформируется
(рис. 45г).
Материал
подчиняется закону Гука. Касательное
напряжение пропорционально углу сдвига.
Крутящие моменты могут меняться вдоль оси бруса. После определ.величин моментов по сечениям строим график эпюру крутящих моментов вдоль оси бруса. Крут.момент считаем положит, если моменты внешних пар сил направлены по часовой стрелке, в этом случае момент внутренних сил упругости направлен против часовой стрелки.
16) Способы определения критической силы (расчет по формуле Эйлера, критические напряжения, расчет критического напряжения по формуле Ф.Ясинского для стальных стержней) Расчет по формулам Эйлера Задачу определения критической силы математически решил Л. Эйлер в 1744 г. Для шарнирно закрепленного с обеих сторон стержня, формула Эйлера имеет вид:
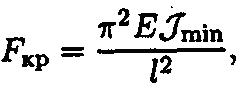
где Е - модуль упругости; Jmin - минимальный осевой момент инерции стержня; - длина стержня. гибкость стержня - величина безразмерная, чем больше гибкость, тем меньше напряжение:
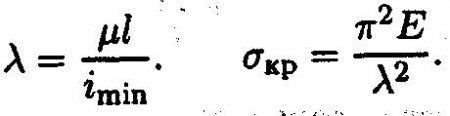
Заметим, что гибкость не зависит от материала, а определяется только геометрией стержня. Для стержней малой гибкости проводится расчет на сжатие Для стержней средней гибкости расчет проводят по формуле Ясинского Для стержней большей гибкости расчет проводят по формуле Эйлера Критическую силу при расчете напряжения по формуле Ясинского можно определить как
Условие устойчивости:
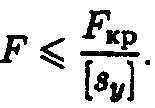
17) Какая из механических характеристик выбирается в качестве предельного напряжения для пластичных и хрупких материалов
для хрупких материалов принимают предел прочности,для пластичных предел текучести,т.л при напряжениях равных пределу текучести,возникают знач.пластичдеф-ции которые недопустимы.