Центробежный момент инерции

Центробежным моментом инерции сечения называется взятая то всей площади сумма произведений элементарных площадок на обе координаты: .

Центробежный момент инерции может быть положительным, отрицательным и равным нулю. Центробежный момент инерции от­носительно осей, проходящих через центр тяжести сечения, равен нулю.

Оси, относительно которых центробежный момент равен нулю, называются главными. Главные оси, проходящие через центр тяже­сти, называют главными центральными осями сечения.

Полярный момент инерции сечения

Полярным моментом инерции сечения относительно некоторой точки (полюса) называется взятая по всей площади сумма произведений элементарных площадок на квадрат их расстояния до этой точки:

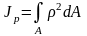
где р — расстояние до полюса (центра поворота) (рис. 25.1).

Поскольку р² = х² - у², получим: полярный момент инерции сечения равен сумме осевых:

J_p = J_x + J_y.

Осевые моменты инерции характеризуют сопротивление сече­ния повороту относительно соответствующей оси.

Полярный момент инерция характеризует сопротивление сече­ния повороту вокруг полюса (начала координат). Единицы измере­ния моментов инерции: м⁴; см⁴; мм⁴.

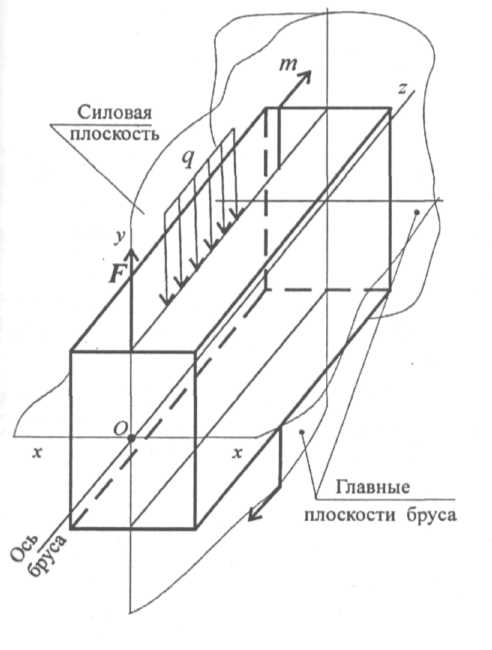
16.Изгиб.Основные определения.Изгибом называется такой вид нагружения, при котором в по­перечном сечении бруса возникает внутренний силовой фактор изгибающий момент.

Брус, работающий на изгиб, называют балкой. Изображен брус, за­крепленный справа (за­щемление), нагруженный внешними силами и мо­ментом. Плоскость, в которой расположены внешние си­лы и моменты, называют силовой плоскостью. Если все силы лежат в одной плоскости, изгиб называют плоским. Если силовая плоскость совпадает с главной плоскостью бруса, изгиб называют прямым. Если силовая плоскость не проходит через главную плоскость бруса, изгиб называют косым изгибом. Изгиб, при котором в поперечном сечении бруса возникает толь­ко изгибающий момент, называется чистым изгибом. Изгиб, при котором в поперечном сечении бруса возникает изги­бающий момент и поперечная сила, называется поперечным изгибом.

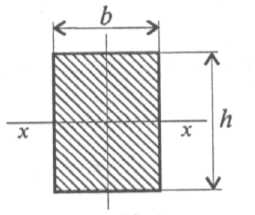
Рациональные сечения при изгибе. Определим рациональные сечения при изгибе, для этого срав­ним моменты сопротивления простейших сечений.

Осевой момент инерции прямоугольника равен . Осевой момент сопротивления прямо­угольника . Сравним сопротивление изгибу двух прямоугольных сечений.

Вариант обладает большим сопротивлением изги­бу при прочих равных условиях.

Осевой момент инерции круга равен .

Осевой момент сопротивления круга .

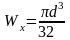Все необходимые расчетные данные (площади, моменты инер­ции и сопротивления) стандартных сечений приводятся в таблицах стандартов (Приложение 1). Для материалов, одинаково работающих на растяжение и сжа­тие, выбирают сечения, симметричные относительно оси, вокруг ко­торой совершается изгиб (рис. 32.7).

Пример Сравним моменты сопротивления двух сечений одинаковой пло­щади: двутавра (рис. 32.7г) и круга (рис. 32.7а).

Двутавр № 10 имеет площадь 12 см², осевой момент инерции 198 см⁴, момент сопротивления 39,7 см³.

Круг той же площади имеет диаметр , осевой момент инерции J_x = 25,12 см⁴, момент сопротивления W_x = 6,2 см³.

.

Сопротивление изгибу у двутавровой балки в шесть раз выше, чем у балки круглого сечения.

Из этого примера можно сделать вывод: сечения прямо­угольные, квадратные, круглые и ромбовидные нерациональны.

Для материалов, обладающих разной прочностью при растяже­нии и сжатии (хрупкие материалы обладают значительно большей прочностью на сжатие, чем на растяжение), выбирают асимметрич­ные сечения тавр, рельс и др.

17.Условие прочности при совместном действии изгиба и кручения. ,

где М_экв — эквивалентный момент.

Эквивалентный момент по гипотезе максимальных касательных напряжений

.

Эквивалентный момент по гипотезе энергии формоизменения

.

18.Что изучает дисциплина "Теор-ая механика".Из каких разделов состоит, их значения.

Техническая механика — комплексная дисциплина. Она включа­ет три раздела: «Теоретическая механика», «Сопротивление мате­риалов», «Детали машин». «Теоретическая механика» — раздел, в котором излагаются основные законы движения твердых тел и их взаимодействия. В разделе «Сопротивление материалов» изучают­ся основы прочности материалов и методы расчетов элементов кон­струкций на прочность, жесткость и устойчивость под действием внешних сил. В заключительном разделе «Технической механики» «Детали машин» рассматриваются основы конструирования и рас­чета деталей и сборочных единиц общего назначения.

Дисциплина «Техническая механика» является обще профессио­нальной, обеспечивающей базовые знания при усвоении специальных дисциплин, изучаемых в дальнейшем.

Теоретическая механика — наука о механическом движении материальных твердых тел и их взаимодействии. Механическое дви­жение понимается как перемещение тела в пространстве и во време­ни по отношению к другим телам, в частности к Земле.

19.Какую плоскость называют силовой. Плоскость, в которой расположены внешние си­лы и моменты, называют силовой плоскостью.Плоскость, проходящая через продольную ось бру­са и одну из главных цен­тральных осей его попе­речного сечения, называ­ется главной плоскостью бруса.Если силовая плоскость совпадает с главной плоскостью бруса, изгиб называют прямым. Если силовая плоскость не проходит через главную плоскость бруса, изгиб называют косым изгибом. Изгиб, при котором в поперечном сечении бруса возникает толь­ко изгибающий момент, называется чистым изгибом. Изгиб, при котором в поперечном сечении бруса возникает изги­бающий момент и поперечная сила, называется поперечным изгибом.

20.Какие внутренние силовые факторы возникают в сечении балки при чистом и поперечном изгибе. При чистом изгибе в поперечном сечении балки возникает только изгибающий момент, постоянный по величине.При поперечном изгибе в сечении возникает изгибающий мо­мент и поперечная сила.Изгибающий момент в произвольном сечении балки численно равен алгебраической сумме моментов всех внешних сил, прило­женных к отсеченной части, относительно рассматриваемого се­чения. Поперечная сила в произвольном сечении балки численно равна алгебраической сумме проекций всех внешних сил, действующих на отсеченной части на соответствующую ось.

21.Какое напряженное состояние возникает в поперечном сечении вала при совместном действии изгиба и кручения. Напишите условие прочности для расчета вала. Условие прочности при совместном действии изгиба и кручения

, где М_экв — эквивалентный момент.

Эквивалентный момент по гипотезе максимальных касательных напряжений .

Эквивалентный момент по гипотезе энергии формоизменения . Особенность расчета валов Большинство валов испытывают сочетание деформаций изгиба и кручения. Обычно валы — прямые брусья с круглым или кольце­вым сечением. При расчете валов касательные напряжения от дей­ствия поперечных сил не учитывают из-за их незначительности. Расчеты проводят по опасным поперечным сечениям. При про­странственном нагружении вала пользуются гипотезой независимо­сти действия сил и изгибающие моменты рассматривают в двух взаимно перпендикулярных плоскостях, а суммарный изгибающий момент определяют геометрическим суммированием.

22.Напишите формулу Эйлера для расчета критической силы и назовите входящие величины и их единицы измерения. Расчет по формуле Эйлера Задачу определения критической силы математиче­ски решил Л. Эйлер в 1744 г.

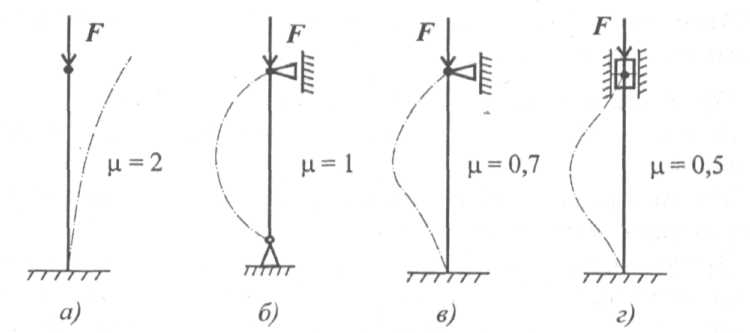
Для шарнирно закрепленного с обеих сторон стержня. формула Эйлера имеет вид

, где Е – модуль упругости; Jmin – минимальный осевой момент инерции стержня; l – длина стержня. Потеря устойчивости происходит в плоскости наи­меньшей жесткости, поэтому в формулу входит минимальный из осевых моментов инерции сечения (Jx или Jy). Формулу распространили на другие формы закрепления стерж­ней, рассмотрев форму потери устойчивости в каждом случае.

Длина стержня заменяется ее приведенным значением, учиты­вающим форму потери устойчивости в каждом случае: l_прив = μд, где μ — коэффициент приведения длины, зависящий от способа за­крепления стержня (рис. 36.3).

Формула для расчета критической силы для всех случаев

.

23.В чем заключается расчет сжатого стержня на устойчивость. Напишите условие устойчивости.Чем отличается допускаемая сжимающая сила от критической. На устойчивость равновесия влияет величина сжимающей силы.

Наибольшее значение сжимающей силы, при которой прямоли­нейная форма стержня сохраняет устойчивость, называют критиче­ской силой. Даже при небольшом превышении критического значе­ния силы стержень недопустимо деформируется и разрушается. Расчет на устойчивость. Расчет на устойчивость заключается в определении допускае­мой сжимающей силы и в сравнении с ней силы действующей: ; ; ,

где F — действующая сжимающая сила;

[F] — допускаемая сжимающая сила, обеспечивает некоторый запас устойчивости;

F_кр — критическая сила;

[s_y] — допускаемый коэффициент запаса устойчивости.

Обычно для сталей [s_y] = l,8 ÷ 3; для чугуна [s_y] = 5; для дерева [Sy] ≈ 2,8.

24.Какое равновесие называется устойчивым.Какие брусья следует рассчитывать на устойчивость. Относительно короткие и массивные стержни рассчитывают на сжатие, т.к. они выходят из строя в результате разрушения или остаточных деформаций. Длинные стержни небольшого поперечного сечения под действием осевых сжимающих сил изгибаются и теряют равновесие. Такие стержни работают на изгиб и сжатие.

Равновесие считают устойчивым, если за счет сил упругости после снятия внешней откло­няющей силы стержень восстановит первоначаль­ную форму (рис. 36.1). Если упругое тело после отклонения от рав­новесного положения не возвращается к исходно­му состоянию, то говорят, что произошла потеря устойчивости, а равновесие было неустойчивым. Потерю устойчивости под действием цен­трально приложенной продольной сжимающей си­лы называют продольным изгибом. На устойчивость равновесия влияет величина сжимающей силы.

25.Что называют гибкостью стержней.Назовите критерии стержней в зависимости от гибкости.

Гибкость стержня — отношение расчетной длины стержня   к наименьшему радиусу инерции   его поперечного сечения.

2 уровень

1)Понятие о силе и системе сил:Сила-это мера механического взаимодействия материальных тел между собой.Измеряется в ньютонах.Силы,действующие на тело,делятся на внешние и внутренние.Внешние силы бывают активные и реактивные.Активные силы вызывают перемещение тела,реактивные стремятся противодействовать перемещению тела под действием внешних сил.Внутренние силы возникают в теле под действием внешних сил.Совокупность сил,действующих на какое-либо тело,наз системой сил.Эквивалентная система сил-действ.также как заданная.Уравновешенной(эквив.нулю)сист.сил наз.такая система,которая,будучи приложенной к телу,не измен.его состояния.

2)Равнодействующая сходящихся сил. Сходящимися называются силы, линии действия которых пересекаются в одной точке.Равнодействующая сходящихся сил равна геометрической сумме этих сил и приложена в точке их пересечения   . Равнодействующая может быть найдена геометрич. способом – построением силового (векторного) многоугольника или аналитич. способом, проектируя силы на оси координат. Проекции силы на оси координат (для плоской сист.):F_x=F×cosa;  F_y=F×cosb=F×sina; проекция >0, если направление составляющей силы совпадает с направл. оси. Условия равновесия сист. сходящихся сил: геометрическое: аналитические: åF_ix=0;  åF_iy=0;  åF_iz=0. 

3)Свойства пар. 1.Пару сил можно перемещать в плоскости ее действ.2.Эквивал.пар-две пары,моменты которых равны,(рис.4.2) эквивал.(действ.их на тело аналог).3.Сложение пар сил-систему пар сил можно заменить равнодейств.парой.Момент равнодейств.пары равен алгебраич.сумме моментов пар,составл.систему.(рис.4.3)

4.Равновесие пар.Для равновесия пар необх.и достаточно,чтобы алгебр.сумма моментов пар системы равнялось 0.

4)Дать понятие: главный вектор системы, главный момент системы.Пучок сил,который можно заменить одной силой наз.главным вектором системы.Образующуюся систему пар сил можно заменить одной эквивал.парой наз.главн моментом системы.

5)Тело вращается вокруг неподвижной оси. Чему равны главный вектор и главный момент действующей на него системы сил.

6) Разновидности опор балочных систем. Какие нагрузки называются сосредоточенными и распределенными: Шарнирно-неподвижная опора препятствует любому поступательному перемещению балки, но дает возможность последней поворачиваться вокруг оси шарнира. Шарнирно-подвижная опора – нижняя часть – поставлена на катки (рисунок 2.28,а), поэтому такая опора не препятствует небольшому перемещению балки в направлении, параллельном опорной поверхности. Жесткая заделка препятствует любому поступательному движению балки и повороту последней в плоскости действия сил. По способу приложения нагрузки делятся на сосредоточенные и распределенные.Если реально передача нагрузки происходит на пренебрежимо малой площадке(в точке),нагрузку наз.сосредоточенной.Часто нагрузка распределена по знач.площадке или линии(давление воды на плотину,давление снега на крышу),тогда нагрузку считают распред.

7)Пространственная сходящаяся система сил, его значение.Простр. сход.система сил-система сил,не лежащих в одной плоскости,линии действия которых пересек.в одной точке. Равнодействующую пространственной системы сил можно определить, построив пространственный многоугольникFΣ = F1 + F2 + F3 + … + Fn. Модуль равнодействующей системы сходящихся сил определим по формуле .Направление вектора равнодействующей определяется углами αч = (FΣ ^ F Σx); αy = (FΣ ^ F Σy); αz = (FΣ ^ F Σz),где    .

8)Произвольная пространственная система сил. Абсолютное значение главного момента Пространственная произвольная система сил – силы не лежат в одной плоскости и их линии действия не пересекаются в одной точке.

9) Уравнения равновесия пространственной системы сил.

10) Основные гипотезы и допущения в сопротивлении материалов.Материалы однородные-в любой точке материалы имеют одинаковые физико-механ.св-ва.Материалы представл.сплошную среду-кристал-кое строение и микроскоп.дефекты не учитыв.Материалы изотропны-механ.св-ва не зависят от направления нагружения.Материалы обладают идеальной упругостью-полностью восстанавл.форму и размеры после сняти нагрузки.

11) Какие силы в сопротивлении материалов считают внешними и внутренними. Какими методами определяют внешние силы. Как называют метод для определения внутренних сил.

Элементы конструкции при работе испытывают внешнее возд-вие,которое оценивается велич.внешней силы.К внешним силам отн.активные силы и реакция опор.Под действ.внешних сил в детали возникают внутр.силы упругости,стремящиеся вернуть телу первонач.форму и размеры.Внешние силы должны быть определены методами теоретич.механики,а внутренние определ.основным методом сопротивления материалов-методом сечений.

12) Формулы для расчета перемещений поперечных сечений бруса при растяжении и сжатии. Используем известные формулы.Закон Гука Откуда Относит.удлинение В рез-те получим зависимость между нагрузкой,размерами бруса и возник.деформацией: где

13)Примеры деталей, работающих на сдвиг (срез) и смятие (ось, болт, шпонки, заклепка одно- и двухсрезная, сварное соединение)

14)Моменты инерции простейших сечений (осевые моменты инерции прямоугольника, полярный момент инерции круга, осевой момент инерции круга и кольца, моменты инерции относительно параллельных осей). Главные оси и главные моменты инерции.

Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении.

Осевой прямоугольника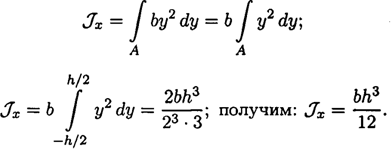 Полярный круг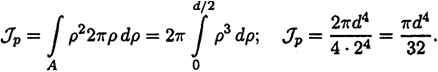 Осевой круга и кольца

Момент параллельных осей

Главные оси-это оси,относительно которых осевые моменты инерции принимают экстрем.знач:миним и максим.Главные центр.моменты инерции рассчитыв.относительно главных осей,проходящих через центр тяжести.

15) Дифференциальные зависимости при прямом поперечном изгибе. Формула для расчета нормальных напряжений при изгибе.

Построение эпюр поперечных сил и изгиб.моментов сущ-но упрощается при исп-нии диф-ных зависимостей между изгиб.моментом,поперечной силой и интенсивн.равномерно распр-ной нагрузки.Поперечная сила равна произ-ной от изгиб.момента по длине балки: Интенсивность раномерно распр-ной нагрузки равна произ-ной от поперечной силы по длине балки: Норм.напряж

16) Устойчивость сжатых стержней. Понятие об устойчивом и неустойчивом равновесии

Равновесие считают устойчивым если за счет сил упругости после снятия внешней отклоняющей силы стержень восстановит первонач.форму.Если упругое тело после отклонения от равновесного положения не возвращается к исходному,то говорят,что произошла потеря устойчивости,а равновесие было не устойчивым.

17) Как определяется мощность при поступательном движении и мощность при вращении

Мощность — работа, выполненная в единицу времени: Единицы измерения мощности: ватты, киловатты, ; 10³ Вт = 1 кВт. Мощность при поступательном движении  Учитывая, что  , получим P = F v_ср cos α,где F – модуль силы, действующей на тело;v_ср – средняя скорость движения тела. Мощность при вращении.Тело движется по дуге радиус г из точки М₁ в точкуМ₂. M₁ ˘ M₂ = φ r Работа силы: W = М_вр.W = M_вр φгде М_вр — вращающий момент. Учитывая,что  , получимP = M_вр ω_ср ,где ω_ср – средняя угловая скорость

18) Какое явление называют текучестью

Текучесть — свойство пластичных металлов и тел при постепенном увеличении давления уступать действию сдвигающих сил и течь подобно вязким жидкостям.Текучесть является свойством, обратным вязкости.Обычно

текучесть обозначается символом φ = 1 / μ или F = 1 / μ.

19) Перечислите характеристики прочности и пластичности, их значения

Хар-ки прочности:предел пропорциональности

предел упругости

предел текучести

предел прочности или временное сопротивление разрыву, Хар-ки пластичности: -максим.удлинение в момент разрыва -максим.осаточное удлинение, -максим.сужение при разрыве, -площадь образца в месте разрыва.

20) Какие площадки и какие напряжения называют главными. Перечислите виды напряженных состояний. Чем характеризуется деформированное состояние в точке

Площадки, по которым касательные напряжения равны нулю, называются главными, а действующие по этим площадкам нормальные напряжения - главными напряжениями. Виды напряженного состояния в точке:а) линейное напряженное состояние – когда два главных напряжения равны нулю (одноосное растяжение или сжатие);б) плоское напряженное состояние – когда только одно из главных напряжений равно нулю;в) объёмное напряженное состояние – когда все три главных напряжения отличны от нуля.Деформированное состояние в точке тела полностью определяется шестью компонентами деформации - тремя относительными линейными деформациями ех, гу, ег и тремя относительными угловыми деформациями уху, у г, ууг.

21) Какую силу при расчете на устойчивость называют критической

КРИТИЧЕСКАЯ СИЛА в теории упругости и пластичности - наименьшая продольная сила, при к-рой возможны как прямолинейная, так н криволинейная формы равновесия первоначально прямолинейного бруса (см. Продольный изгиб ).К. с. зависит от механич. характеристик материала бруса, формы его поперечного сечения, условий закрепления, а при пластич. деформациях - и от податливости конструкции, элементом к-рой он является. К. с. упругого бруса определяется ф-лой Эйлера: где Е - модуль продольной упругости материала, I - наим. значение центр. момента инерции поперечного сечения, l - длина бруса,  - коэф., учитывающий условия закрепления.

22) Напишите формулу Ф.Ясинского для расчета критического напряжения

В частности, Ф.С. Ясинский предложил сле­дующую формулу для критических по устойчивости напряжений: где a, b - постоянные, зависящие от материала, так для стали Ст.3 a = 3,1×10⁵ кН/м² ,b = 11,4×10² кН/м².

23) Что такое эквивалентное напряжение. Напишите формулы расчета эквивалентных напряжений. Эквивалентное напряжение (σэкв) – это напряжение, под действием которого материал в условиях простого растяжения-сжатия оказывается в равноопасном состоянии с рассматриваемым сложным напряженным состоянием. Эквивалентные напряжения при объемном напряженном состоянии:

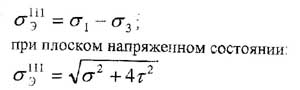
24) Укажите формулу Д.Журавского для расчета касательных напряжений для балки квадратного сечения

Формула Журавского для касательных напряжений: От сдвига возникают касательные напряжения, которые находятся по формуле Журавского где Q – поперечная сила;   – статический момент отсеченной части поперечного сечения относительно оси х, где  – площадь отсеченной части поперечного сечения; Y_o – расстояние от центра тяжести отсеченной части поперечного сечения до оси x;   – главный момент инерции.

25) Напишите условие прочности при изгибе

Условия прочности при изгибе по нормальным и касательным напряжениям имеют вид где W_х – осевой момент сопротивления;

3 уровень