1. Задачи теор.мех. Теоретическая механика — наука о механическом движении материальных твердых тел и их взаимодействии. Механическое дви­жение понимается как перемещение тела в пространстве и во време­ни по отношению к другим телам, в частности к Земле.

Для удобства изучения теоретическую механику подразделяют на статику, кинематику и динамику.

Статика изучает условия равновесия тел под действием сил.

Кинематика рассматривает движение тел как перемещение в пространстве; характеристики тел и причины, вызывающие движе­ние, не рассматриваются.

Динамика изучает движение тел под действием сил.

В отличие от физики теоретическая механика изучает законы движения некоторых абстрактных абсолютно твердых тел: здесь материалы, форма тел существенного значения не имеют. При дви­жении абсолютно твердое тело не деформируется и не разрушается. В случае, когда размерами тела можно пренебречь, тело заменяют материальной точкой. Это упрощение, принятое в теоретической ме­ханике, значительно облегчает решение задач о движении.

2.Аксиомы статики.В результате обобщения человеческого опыта были установле­ны общие закономерности механического движения, выраженные в виде законов и теорем. Все теоремы и уравнения статики выводятся из нескольких исходных положений. Эти положения называют акси­омами статики.

Первая аксиома

Под действием уравновешенной системы сил абсолютно твердое тело или материальная точка находятся в равновесии или движутся равномерно и прямолинейно (закон инерции).

Вторая аксиома

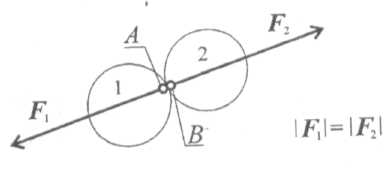
Две силы, равные по модулю и направленные по одной прямой в разные стороны, уравновешиваются (рис. 1.2). Рис. 1.2

Третья аксиома

Не нарушая механического состояния тела, можно добавить или убрать уравновешенную систему сил (принцип отбрасывания систе­мы сил, эквивалентной нулю)

Четвертая аксиома (правило параллелограмма сил)

Равнодействующая двух сил, прило­женных в одной точке, приложена в той же точке и является диагональю паралле­лограмма, построенного на этих силах как на сторонах .

Вместо параллелограмма можно по­строить треугольник сил: силы вычерчи­вают одну за другой в любом порядке; равнодействующая двух сил соединяет начало первой силы с концом второй.

Пятая аксиома

При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие.

Силы действующие и противо­действующие всегда приложены к разным телам, поэтому они не урав­новешиваются.

Силы, с которыми два тела дей­ствуют друг на друга, всегда равны по модулю и направлены вдоль одной прямой в разные стороны.

3.Какая сис-ма называется сис-ой сходящихся сил.

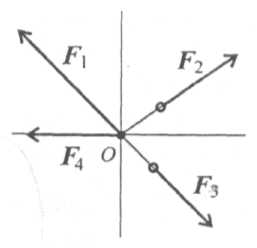
Система сил, линии действия которых пе­ресекаются в одной точке, называется сходя­щейся (рис. 2.1).

Необходимо определить равнодействую­щую системы сходящихся сил (F₁; F₂; F₃; …; F_n), n — число сил, входящих в систему.

По следствию из аксиом статики, все си­лы системы можно переместить вдоль линии действия, и все силы окажутся приложенными в одной точке.

4.Дать понятие :пара сил, плечо пары, момент силы относительно точки.

Парой сил называется система двух сил, равных по модулю, параллельных и направлен­ных в разные стороны.

Сила, не проходящая через точку крепления тела, вызывает вра­щение тела относительно точки, поэтому действие такой силы на тело оценивается моментом.

Момент силы относительно точки числен­но равен произведению модуля силы на рассто­яние от точки до линий действия силы. Перпен­дикуляр, опущенный из точки на линию дей­ствия силы ,называется плечом силы. 5.Частные случаи приведения сис-мы сил к точке.

При приведении системы сил к точке возможны следующие ва­рианты:

1. Fгл = 0 МглО ≠ 0	тело вращается вокруг неподвижной оси.
2. МглО = 0 Fгл ≠ 0; Fгл = FΣ	тело движется прямолинейно ускоренно.
3. МглО = 0 Fгл = 0	тело находится в равновесии.

6. Первая,третья,пятая аксиома статики. В результате обобщения человеческого опыта были установле­ны общие закономерности механического движения, выраженные в виде законов и теорем. Все теоремы и уравнения статики выводятся из нескольких исходных положений. Эти положения называют акси­омами статики.

Первая аксиома

Под действием уравновешенной системы сил абсолютно твердое тело или материальная точка находятся в равновесии или движутся равномерно и прямолинейно (закон инерции).

Вторая аксиома

Две силы, равные по модулю и направленные по одной прямой в разные стороны, уравновешиваются

Третья аксиома

Не нарушая механического состояния тела, можно добавить или убрать уравновешенную систему сил (принцип отбрасывания систе­мы сил, эквивалентной нулю)

Четвертая аксиома (правило параллелограмма сил)

Равнодействующая двух сил, прило­женных в одной точке, приложена в той же точке и является диагональю паралле­лограмма, построенного на этих силах как на сторонах (рис. 1.4).

Вместо параллелограмма можно по­строить треугольник сил: силы вычерчи­вают одну за другой в любом порядке; равнодействующая двух сил соединяет начало первой силы с концом второй.

Пятая аксиома

При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие

7.Влияние точки приведения. Точка приведения выбрана произвольно. При изменении поло­жения точки приведения величина главного вектора не изменится.

Величина главного момента при переносе точки приведения из­менится, т. к. меняются расстояния от векторов-сил до новой точки приведения.

С помощью теоремы Вариньона о моменте равнодействующей можно определить точку на плоскости, относительно которой глав­ный момент равен нулю. Тогда произвольная плоская система сил может быть заменена одной силой.

Эту силу называют равнодействующей системы сил.

Численно равнодействующая равна главному вектору системы сил, но приложена в другой точке, относительно которой главный момент равен нулю. Равнодействующую принято обозначать F%.

Численно ее значение определяется так же, как главный вектор системы сил:

F_Σ = F_гл;

.

где d — расстояние от выбранной точки приведения до точки при­ложения равнодействующей;

М_гл — величина главного момента относительно выбранной точки приведения;

F_гл — величина главного вектора системы сил.

8.Условие равновесия произвольной плоской сис-мы сил. 1. При равновесии главный вектор системы равен нулю (F_гл = 0).

Аналитическое определение главного вектора приводит к выводу:

где F_kx и F_ky — проекции векторов на оси координат.

2. Поскольку точка приведения выбрана произвольно, ясно, что при равновесии сумма моментов сил системы относительно любой точки на плоскости должна равняться нулю:

где А и В — разные точки приведения.

Условие равновесия произвольной плоской системы сил может быть сформулировано следующим образом:

Для того чтобы твердое тело под действием произвольной плоской системы сил находилось в равновесии, необходимо и до­статочно, чтобы алгебраическая сумма проекций всех сил систе­мы на любую ось равнялась нулю и алгебраическая сумма момен­тов всех сил системы относительно любой точки в плоскости действия сил равнялась нулю.

Получим основную форму уравнения равновесия:

{		}	уравнения моментов.

Теоретически уравнений моментов можно записать бесконечное множество, но практически доказано, что на плоскости можно соста­вить только три независимых уравнения моментов и при этом три точки (центры моментов) не должны лежать на одной линии.

Таким образом, имеем пять независимых уравнений равновесия.

Практически для решения задач на плоскости достаточно трех уравнений равновесия. В каждом конкретном случае используются уравнения с одним неизвестным.

Для разных случаев используются три группы уравнений рав­новесия.

Первая формула уравнений равновесия:	{
Вторая формула уравнений равновесия:	{
Третья формула уравнений равновесия:	{

Для частного случая, если уравновешенная система параллельных сил, можно составить только два уравнения равновесия:

Ось О_х системы координат параллельна линии действия сил.

9.Чем отличается главный вектор от равнодействующей плоской сис-мы произвольно расположенных сил. Линии действия произвольной системы сил не пересекаются в одной точке, поэтому для оценки состояния тела такую систему следует упростить. Для этого все силы системы переносят в одну произ­вольно выбранную точку — точку приведения. Применяют теорему Пуансо. При любом переносе силы в точку, не лежащую на линии ее действия, добавляют пару сил.

Дана плоская система произвольно расположенных сил.

Переносим все силы в точку О. Получим пучок сил в точке О, ко­торый можно заменить одной силой — главным вектором системы. Образующуюся систему пар сил можно заменить одной эквивалент­ной парой — главным моментом системы.

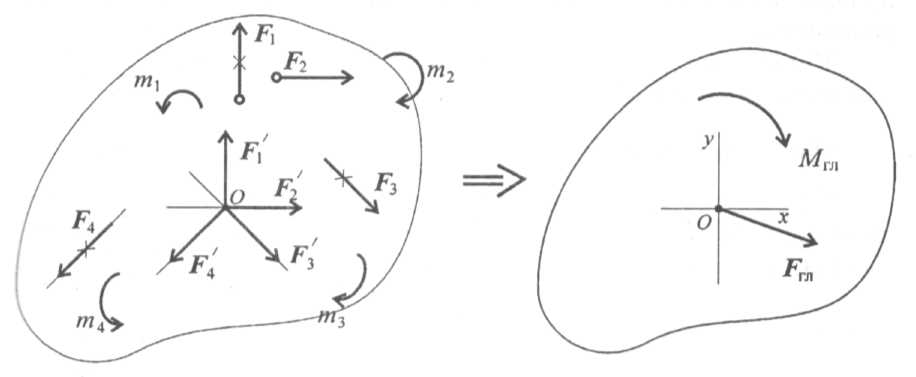
Главный вектор равен геометрической сумме векторов произ­вольной плоской системы сил. Проецируем все силы системы на оси координат и, сложив соответствующие проекции на оси, получим проекции главного вектора.

;

Таким образом, произвольная плоская система сил приводит­ся к одной силе (главному вектору системы сил) и одному моменту (главному моменту системы сил).

Систему сил, действующих на тело, можно заменить одной рав­нодействующей, действующей так, как система сил.

10.Тело движется равномерно и прямолинейно(равновесие).Чему равны главный вектор и главный момент сис-мы. Из законов меха­ники следует, что твердое тело, на которое действуют взаимно уравновешенные внешние силы, может не только находиться в покое, но и совершать движение, которое мы назовем движением «по инер­ции». Таким движением будет, например, поступательное равномерное и прямолинейное движение тела.

Отсюда получаем два важных вывода: 1) Условиям равновесия статики удовлетворяют силы, действующие как на покоящееся тело, так и на тело, движущееся «по инерции». 2) Уравно­вешенность сил, приложенных к свободному твердому телу, является необходимым, но не достаточным условием равновесия (покоя) самого тела; в покое тело будет при этом находиться лишь в том случае, если оно было в покое и до момента приложения к нему уравнове­шенных сил.

Для равновесия приложенной к твердому телу системы сходя­щихся сил необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю. Условия, которым при этом должны удовле­творять сами силы, можно выразить в геометрической или аналити­ческой форме.

Для того чтобы твердое тело под действием произвольной плоской системы сил находилось в равновесии, необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил системы на любую ось равнялась нулю и алгебраическая сумма моментов всех сил системы относительно любой точки в плоскости действия сил равнялась нулю.

11.Механические свойства материалов. Прочность — способность не разрушаться под нагрузкой. Жесткость — способность незначительно деформироваться под нагрузкой.

Выносливость — способность длительное время выдерживать временные нагрузки.

Устойчивость — способность сохранять первоначальную форму упругого равновесия.

Вязкость — способность воспринимать ударные нагрузки.

Виды расчетов. Расчет на прочность обеспечивает неразрушение конструкции.

Расчет на жесткость обеспечивает деформации конструкции год нагрузкой в пределах допустимых норм.

Расчет на выносливость обеспечивает необходимую долговечность элементов конструкции.

Расчет на устойчивость обеспечивает сохранение необходимой формы равновесия и предотвращает внезапное искривление длинных стержней.

Для обеспечения прочности конструкций, работающих при ударных нагрузках (при ковке, штамповке и подобных случаях), про­водятся расчеты на удар.

12.Что называют механическим напряжением. Состояние упруго деформированного тела характеризуют величиной σ, называемой механическим напряжением. Механическим напряжением … называется величина, характеризующая действие внутренних сил в деформированном твердом теле.  Как по отношению к площадке направлены нормальное и касательное напряжение. Как они обозначаются. Если внутренняя сила действует перпендикулярно сечению, то напряжение называется нормальным sн (например, при деформации продольного растяжения). Если же эта сила действует параллельно сечению, то напряжение называют касательным sк (например, при деформации сдвига).

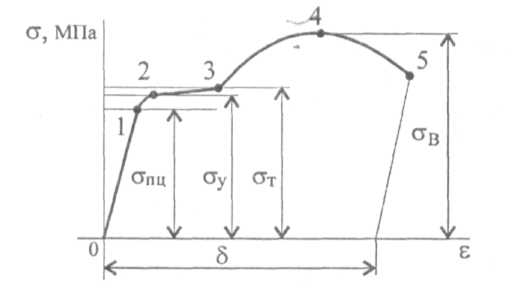
1.13.Механические характеристики. При построении приведенной диаграммы рассчитываются величины, имеющие условный характер, усилия в каждой из точек делят на величину начальной площади поперечного сечения,

хотя в каждый момент идет деформация и площадь образца уменьшается. Приведенная диаграмма растяжения не зависит от абсолютных размеров образца. О сновные характеристики прочности: - предел пропорциональности ;- предел упругости ; - предел текучести ; - предел прочности, или временное сопротивление разрыву, , где - начальная площадь сечения.