7.5. Оптимальный одношаговый алгоритм оценивания параметров

Значительный интерес представляют упрощённые варианты алгоритмов текущего рекуррентного оценивания, где не используются не только операции обращения матриц, но и какие-либо иные матричные операции. Один из таких алгоритмов может быть получен из алгоритма «с постепенным забыванием» (7.15), (7.21), (7.22), если в (7.21) приравнять матрицу единичной матрице. Сформированный подобным образом т.к. «оптимальный одношаговый алгоритм» может быть записан в виде единой формулы

(7.23)

или в скалярной форме

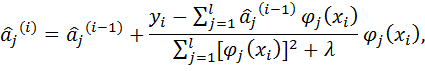
(7.24)

Д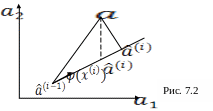 ля понимания метода оценивания (4.68) может служить геометрическая интерпретация. На рис. 4.2 показана схема уточнения оценки на i – м шаге работы алгоритма, относящаяся к случаю, когда модель процесса содержит всего два параметра .

Согласно выражению (7.23) для получения новой оценки из точки делается шаг в направлении параллельном вектору входных воздействий . Можно показать, что при , величина шага подобрана так, что точка оказывается ближайшей (на выбранной прямой) к точке истинных параметров . Из рис. 7.2 видно, что при подобном способе уточнения оценок расстояние между точками и меньше расстояния между и , что является необходимым признаком сходимости алгоритма оценивания. Заметим также, что если вектор очередных входных воздействий не изменит своего направления по отношению к , то точка совпадёт с точкой , а значит, дальнейшего уточнения оценок не произойдёт. Таким образом, важным условием сходимости алгоритма оценивания (7.23) является изменение во времени направления вектора входных воздействий.

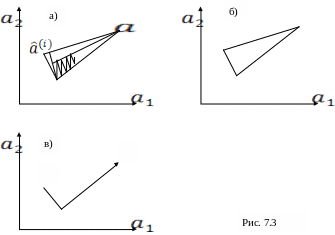
Скорость сходимости рассматриваемого алгоритма оценивания тем выше, чем радикальней изменяется от шага к шагу направление вектора входных воздействий. Иллюстрацией этого может служить рис. 7.3. Наиболее благоприятна ситуация, когда векторы входов ортогональны, т.е. перпендикулярны друг другу. В таком случае для двухфакторной модели алгоритм сходится из начальной точки за два шага.

П

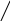
ри в выбранном направлении делается более «осторожный», т.е. более короткий шаг.

а – малый угол (медленная сходимость);

б – большой угол (быстрая сходимость);

в – прямой угол (максимальная скорость сходимости).

При этом оценка улучшается по сравнению с предшествующей оценкой , но не оптимальным образом (см. рис. 7.2). Тем не менее, использование целесообразно при наличии измерительных помех, т.к. определённая степень недостоверности получаемой информации требует соответствующей осторожности.

7.6. Особенности построения моделей тп в промышленных условиях

При построении математических моделей действующих ТП наиболее привлекает возможность текущего оценивания параметров моделей без нарушения нормального хода процесса. Оказывается, однако, что практическая реализация методов построения моделей в режиме нормальной эксплуатации путём обработки данных т.н. пассивного эксперимента наталкивается на серьёзные трудности.

Рассмотрим в качестве поясняющего примера построение регрессионной модели активности цемента, получаемого путём смешивания клинкера и добавок. Главными факторами, определяющими активность цемента , являются активность клинкера и его доля в смеси . Пусть модель, записанная в отклонениях от номинального режима, имеет вид

, (7.25)

где и - подлежащие оценке неизвестные параметры.

Казалось бы, наиболее естественный путь определения коэффициентов модели (7.25) заключается в сборе по заводским журналам достаточно представительной выборки данных об изменениях факторов и , а также отклике и определения и с помощью МНК или какого-либо иного из рассмотренных методов оценивания параметров. Проанализируем возможные результаты такого подхода.

Для рассматриваемого процесса является нерегулируемым внешним возмущением, в то время как может целенаправленно изменяться машинистом цементных мельниц, в которых происходит одновременное измельчение и смешивание компонентов цементной шихты. Рассмотрим две близких к реальности модели поведения машиниста.

Первая, более примитивная, стратегия, характерная для менее опытных работников, состоит в том, что после ввода ТП в установившийся режим машина в течение длительного времени не изменяет уставки дозирующих органов. В этом случае один из входов идентифицируемой модели поддерживается на нулевом уровне, а стало быть, коэффициент не может быть найден никаким методом оценивания параметров.

Вторая стратегия характерна для опытных машинистов, которые стремятся в ходе процесса изменять дозировку компонентов таким образом, чтобы компенсировать влияние внешних возмущений на качество цемента. Сопоставляя данные лаборатории о содержании в клинкере свободного оксида кальция с визуальной оценкой клинкера, машинист приблизительно оценивает изменения качества клинкера и, руководствуясь накопленным опытом, изменяет дозировку таким образом, чтобы постоянно выполнялось условие . Если бы были точно известны коэффициенты модели (7.25), то регулирование дозировок, очевидно, следовало бы проводить по правилу:

При отсутствии такого рода данных машинист использует сходный закон регулирования:

(7.26)

подбирая коэффициент усиления С опытным путём.

Рассматривая условия сходимости алгоритмов текущего оценивания параметров (7.23), мы отмечали, что такая сходимость обеспечивается лишь в том случае, если вектор входных воздействий существенным образом изменяет во времени своё направление. Ясно, однако, что регулирование процесса приводит к нарушению этого необходимого условия сходимости: действительно, согласно (7.26) входные воздействия и пропорциональны, т.е. вектор имеет постоянное направление, определяемое значением параметра С.

Итак, два основных фактора, затрудняющих текущее оценивание параметров регрессионных моделей в режиме нормальной эксплуатации, это малый диапазон изменения и взаимная зависимость входных воздействий. Вследствие этого для получения достаточно точных математических моделей ТП, как правило, необходимы специально организуемые в рамках активного эксперимента достаточно сильные входные воздействия. Задача построения наиболее точных моделей технологических зависимостей при ограниченном объёме эксперимента является предметом теории планирования эксперимента. В типовых ситуациях исследователю не приходится решать самостоятельную задачу синтеза оптимального плана, а достаточно обратиться к опубликованным таблицам планов эксперимента. В таблицах приведены оптимальные или близкие к ним планы для наиболее часто встречающихся линейных, квадратичных и иных типов полиномиальных моделей. Таблицы составлены применительно к стандартным типам ограничений, из которых наиболее употребительны условия вида

(7.27)

ограничивающие диапазон изменения каждого из входных воздействий отрезком

В качестве примера использования табличных планов служит эксперимент по оценке влияния рецептурно-технологических факторов на прочность цемента, проведённый на одном из цементных заводов. Квадратичная четырёхфакторная модель активности цемента 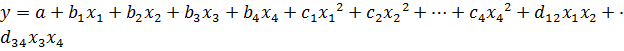(содержащая 15 подлежащих оцениванию параметров) была построена в результате испытаний, проведённых по плану так называемого полного факторного эксперимента типа . Данные об интервалах варьирования каждого из четырёх факторов сведены в табл. 7.1.

Табл. 7.1

Уровни факторов и интервалы их варьирования	Факторы
	Активность клинкера, мПа	Содержание гипса в цементе, %	Содержание добавки в цементе, %	Тонкость помола цемента (остаток на сите), %
Номинальный уровень	45,0	2,75	10	10
Интервал варьирования	±4,0	±0,75	±5	±5
Верхний уровень	49,0	3,50	15	15
Нижний уровень	41,0	2,00	5	5

План эксперимента, получаемый всевозможными комбинациями крайних уровней исследуемых четырёх факторов, приведён в табл. 7.2.

Табл. 7.2

Номер опыта	Факторы
1 2 3 4 5 6 7 8	-1 -1 -1 -1 -1 -1 -1 -1	-1 -1 -1 -1 1 1 1 1		-1 -1 1 1 -1 -1 1 1	-1 1 -1 1 -1 1 -1 1

Номер опыта	Факторы
9 10 11 12 13 14 15 16	1 1 1 1 1 1 1 1	-1 -1 -1 -1 1 1 1 1	-1 -1 1 1 -1 -1 1 1	-1 1 -1 1 -1 1 -1 1

При реализации этого плана каждый из 16 запланированных опытов проводится согласно схеме, приведённой в соответствующей строке матрицы планирования. Табличные планы составлены для моделей с нормированными факторами, т.е.

(7.28)

где – обозначение номинального (режимного) значения j-го фактора; – допустимое отклонение от номинала.

Чтобы перейти от табличных значений к значениям реальных факторов, достаточно воспользоваться формулой .

Например, план опыта №9 состоит в том, что активность клинкера поддерживается на верхнем уровне 49,0 мПа в то время как содержание гипса в цементе, содержание добавки в цементе и тонкость помола цемента фиксируются на нижнем уровне и составляют соответственно 2, 5 и 5%.

Рассмотренная схема планирования активного эксперимента относится к ситуации, когда оценивание параметров регрессионной модели производится после окончания эксперимента с использованием всей полученной информации. При этом план эксперимента составляется заранее до его проведения. В идеале он формируется в результате решения задачи минимизации дисперсий ошибок оценивания параметров модели (7.8). Оценивание параметров производится по схеме МНК (7.12) – (7.14).

Ранее были изучены также схемы текущего оценивания для моделей квазистационарных ТП, характеристики которых могут изменяться во времени. Для применяемых в этом случае рекуррентных процедур оценивания типа (7.15) возникает сходная проблема текущего планирования активного эксперимента, когда план составляется на один или несколько шагов вперёд. В последнем случае в каждом цикле планирования можно использовать стандартные планы, применяемые при построении моделей статических объектов. В частности, при построении распространённого типа линейных моделей

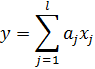
в условиях ограничений

(7.29)

наибольшее быстродействие в ходе отслеживания изменяющихся параметров обеспечивается при подаче в каждом цикле планирования последовательности l нормированных входных воздействий , удовлетворяющих требованиям ортогональности:

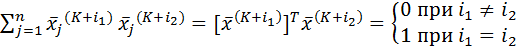(7.30)

где .

Нетрудно убедиться, что условию (7.30) удовлетворяет, например, последовательность

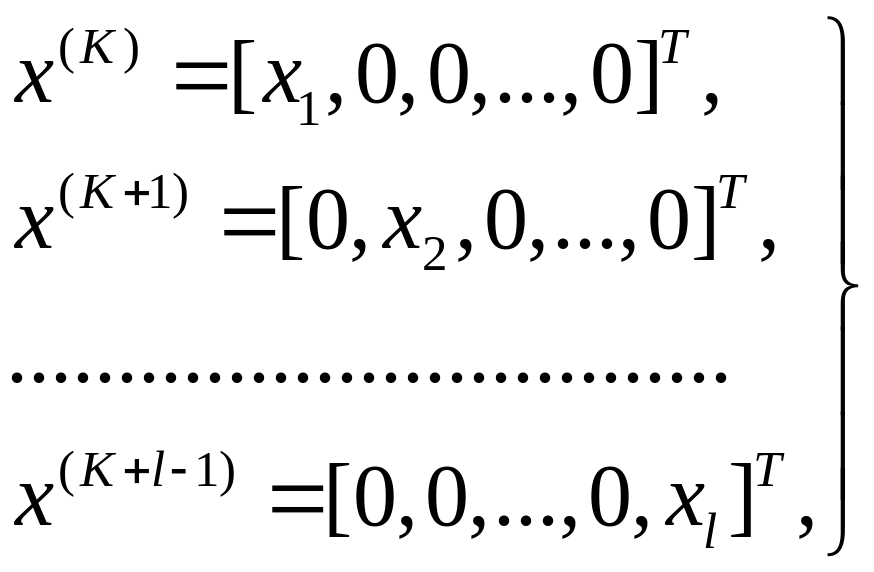(7.31)

где .

Определим величину ошибки слежения за переменными параметрами a при использовании одношагового оптимального алгоритма оценивания (7.23) в случае подачи на вход системы воздействий типа (7.31). Несложно показать, что при этом оценка каждого компонента вектора параметров уточняется один раз в l тактов. При отсутствии измерительных ошибок и в момент уточнения оценка в точности равна истинному значению параметра . В последующие моменты оценка остаётся прежней вплоть до очередного уточнения, в то время как величина оцениваемого параметра может изменяться. Пусть – величина максимального изменения параметра за один шаг, тогда максимальная погрешность оценивания составит величину

Если выход модели измеряется с максимальной погрешностью , то появляется дополнительная составляющая погрешности оценивания, так что

(7.32)

Последняя формула показывает, что погрешность оценивания тем больше, чем выше скорость дрейфа параметра и чем больше число оцениваемых параметров l. Из неё также следует, что погрешность оценивания тем меньше, чем ниже уровень измерительных помех и чем выше уровень входных воздействий

Подводя итог, изложению основных идей планирования экспериментов с целью построения регрессионных моделей ТП, следует сделать вывод, что применительно к режиму нормальной эксплуатации как пассивный, так и активный эксперименты имеют сильные и слабые стороны. Пассивный эксперимент не препятствует нормальному ходу ТП, но не позволяет получить достаточно точные модели. Активный эксперимент позволяет хорошо отслеживать изменения параметров регрессионных моделей, но в период проведения активного эксперимента качество продукта снижается из-за сильной «раскачки».

Противоречия, возникающие вследствие стремления, с одной стороны, лучше узнать технологический объект, а с другой стороны – наиболее полным образом использовать полученные знания для оптимизации или стабилизации его показателей, определяют дуальный характер управления квазистационарными ТП. Ближайшая перспектива практического решения проблемы дуального управления заключается в рациональным образом организованном чередовании периодов активного изучения ТП и подстройки его математической модели с периодами (по возможности более длительными) оптимизации и стабилизации режима, осуществляемых с использованием построенных математических моделей. Блок-схема подробной системы текущей оптимизации кавзистационарного ТП приведена ниже. Наблюдая за входными характеристиками процесса, подсистема анализа его функционирования при обнаружении ухудшения показателей качества продукции передаёт функции выработка управляющих воздействий подсистеме текущей идентификации математический модели. После реализации серии «раскачивающих» воздействий и обновления модели подсистема оптимизации и стабилизации режима ТП вновь берёт на себя управления.